|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ahlberg J.H., Nilson E.N., WAlsh J.L. Ч The Theory of Splines and Their Applications |
|
|
 |
| ѕредметный указатель |
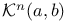 , definition of 75 , definition of 75
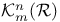 , definition of 275 , definition of 275
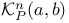 , definition of 75 , definition of 75
Ahlberg, J.R. 2 3 4 5 6 7 70 78 136 140 142 237
Atteia, M. 6
Auslender, S. 143
Beam theory 1 3 77
Beamfit see УCubic splineФ
Bellman, R.E. 56
Best approximation property 4
Best approximation property for cubic splines 16Ч19 77Ч78
Best approximation property for doubly cubic splines 244Ч245
Best approximation property for generalized uplines 200Ч201
Best approximation property for polynomial splines 157Ч159
Bicubic splines 5Ч6 (see also УDoubly cubic splinesФ)
Birkhoff, G. 4 5 29 237
Birkhoff, G., definition of 275
Canonical mesh bases for cubic splines 101Ч103
Canonical mesh bases for doubly cubic splines 249
Canonical mesh bases for generalized splines 219Ч220 275
Canonical mesh bases for polynomial splines 179Ч182
Cardmal splines 52Ч53 245Ч247 251Ч254
Circulant matrix 36 133 148Ч149
Convergence in norm for cubic splines 98Ч101
Convergence in norm for doubly cubic splines 247Ч248
Convergence in norm for generalized splines 214Ч219
Convergence in norm for polynomial splines 176Ч179
Convergence properties 4Ч5
Convergence properties for cubic splines 19Ч34 61Ч74 87Ч96
Convergence properties for doubly cubic splines 247Ч248
Convergence properties for generalized splines 201Ч212 274
Convergence properties for polynomial splines 135Ч143 148Ч152 166Ч174
Coons surfaces 262Ч264
Cubic splines 1 9Ч108
Cubic splines 1, best approximation property 16Ч19 77Ч78
Cubic splines 1, canonical mesh bases 101Ч103
Cubic splines 1, cardinal splines 52Ч58
Cubic splines 1, convergence 19Ч34 61Ч74 87Ч96
Cubic splines 1, convergence m norm 93Ч101
Cubic splines 1, curve fitting 50Ч52
Cubic splines 1, deficiency of 24
Cubic splines 1, defining values 82 97
Cubic splines 1, end conditions 11 13Ч14 50
Cubic splines 1, equal intervals 9 34Ч42
Cubic splines 1, equations for 10Ч16 84Ч87
Cubic splines 1, existence 16Ч19 61Ч74 84
Cubic splines 1, first integral relation 77Ч82
Cubic splines 1, fundamental identity 78Ч79
Cubic splines 1, Hilbert space theory of 97Ч107
Cubic splines 1, integral equations 57Ч59
Cubic splines 1, linear functionals 103Ч107
Cubic splines 1, minimum norm property 75Ч77
Cubic splines 1, orthogonality 97Ч101
Cubic splines 1, parametric splines 51
Cubic splines 1, periodic cubjc splines 10
Cubic splines 1, second integral relation 89Ч91
Cubic splines 1, simple cubic splines 78
Cubic splines 1, spline-on-a-spline 44 48Ч50
Cubic splines 1, type I 75
Cubic splines 1, type I' 75
Cubic splines 1, type II 75
Cubic splines 1, type IIТ 75
Cubic splines 1, uniqueness 16Ч19 82Ч83
Cumulative chord length 51 254Ч262
Curve fitting 1Ч2 50Ч52 143
Dahlqulst, G. 233
Davis, P.J. 19 220
de Eoor, C. 4 5 6 7 29 237
Deficiency of a spline 7
Deficiency of a spline for cubic splines 24
Deficiency of a spline for generalized splines 191Ч192
Deficiency of a spline for polynomial splines 123 143Ч147 157 163Ч164
Deficiency of a spline for quintic splines 123 143Ч148
Defining values 82 97 175 235
Degree of a spline 109
Differential equations 52Ч57 228Ч233
Differentiation see УNumerical differentiationФ
Direct products (of Hubert spaces) 249
Doubly cubic splines 5 235Ч264
Doubly cubic splines, 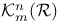 275 275
Doubly cubic splines, best approximation property 244Ч245
Doubly cubic splines, canonical mesh bases 249
Doubly cubic splines, cardinal splines 245Ч247 251Ч254
Doubly cubic splines, convergence 247Ч248
Doubly cubic splines, convergence in norm 250
Doubly cubic splines, defining values 235
Doubly cubic splines, doubly periodic splines 236
Doubly cubic splines, existence 239 243Ч244
Doubly cubic splines, first integral relation 242
Doubly cubic splines, fundamental identity 240Ч242
Doubly cubic splines, Hilbeit space theory 249Ч251
Doubly cubic splines, irregular regions 254Ч258
Doubly cubic splines, minimum norm property 242Ч243
Doubly cubic splines, partial differential equations 251Ч254
Doubly cubic splines, partial splines 237Ч239
Doubly cubic splines, second integral relation 248
Doubly cubic splines, simple doubly cubic splines 235
Doubly cubic splines, surfaces 256Ч262
Doubly cubic splines, type I 235Ч236
Doubly cubic splines, type I' 236
Doubly cubic splines, type II 236
Doubly cubic splines, type II' 236
Doubly cubic splines, uniqueness 239 243Ч244
Doubly periodic splines 236
Eigenvalue problem 57Ч58 228Ч230
Elastica 1 3
End conditions, cubic splines 11 13Ч14 50
End conditions, curve fitting 50
End conditions, modified type k 170
End conditions, polynomial splines 122Ч123 158
End conditions, type I 75 113 193Ч194 235Ч236
End conditions, type I' 75 113 193Ч194 236
End conditions, type II 75 313 193Ч194 236
End conditions, type II' 75 113 193Ч194 236
End conditions, type k 167Ч168 194
Equal intervals, cubic splines 9 34Ч42
Equal intervals, polynomial splines 124Ч135 148Ч152
Existence of splines 2
Existence of splines, of cubic splines 16Ч19 61Ч74 84
Existence of splines, of doubly cubic splines 239 243Ч244
Existence of splines, of generalized splines 199Ч200 272Ч274
Existence of splines, of polynomial splines 132Ч335 165Ч866
Explicit type 269Ч270
Fejer, L. 23Ч24 147Ч148
First integral relation 3
First integral relation for cubic splines 77Ч82
First integral relation for doubly cubic splines 242
First integral relation for generalized sphnes 193Ч195 270 271
First integral relation for polynomial sphnes 155Ч156
Fundamental identity 392Ч193 267Ч269
Fundamental identiy for cubic splines 78Ч79
Fundamental identiy for doubly cubic splines 240Ч242
Fundamental identiy for generalized splines 192Ч193 267Ч269
Fundamental identiy for polynomial splines 154Ч155
Garabedian, H. 5 237
Generalized splines 6 191Ч233 265Ч276
Generalized splines, best approximation property 200Ч201
Generalized splines, canonical mesh bases 239Ч220 275
Generalized splines, convergence 203Ч212 274
Generalized splines, convergence in norm 234Ч239
Generalized splines, deficiency of 191Ч192
Generalized splines, differential equations 228Ч233
Generalized splines, equations for 197Ч399
Generalized splines, existence 199Ч200 272Ч274
Generalized splines, explicit type 269Ч270
Generalized splines, first integral relation 393Ч195 270Ч271
| Generalized splines, Hilbert space theory 213Ч233 275Ч276
Generalized splines, integral equations 230Ч232
Generalized splines, linear functional 220Ч233 275Ч276
Generalized splines, minimum norm property 195Ч196 271Ч272
Generalized splines, numerical integration 224Ч228
Generalized splines, order of 393
Generalized splines, orthogonality 238
Generalized splines, partial differential equations 276
Generalized splines, partial splines 273
Generalized splines, Peano kernels 220Ч224
Generalized splines, periodic splines 194
Generalized splines, second integral relation 204Ч206
Generalized splines, simple splines 194
Generalized splines, strong interpolation 270
Generalized splines, two-dimensional 265Ч276
Generalized splines, type I 193Ч194
Generalized splines, type I' 193Ч194
Generalized splines, type II 193Ч194
Generalized splines, type II' 193Ч194
Generalized splines, type k 394
Generalized splines, uniqueness 196Ч197 271Ч272
Generalized splines, uniqueness property 272
GershgormТs theorem 16
Golomb, M. 7Ч8
Greville, T.N.E. 4 6 105
heterogeneous splines 394
Hilbert space theory 3Ч4
Hilbert space theory for cubic splines 97Ч107
Hilbert space theory for doubly cubic splines 249Ч251
Hilbert space theory for generalized splines 213Ч233 275Ч276
Hilbert space theory for polynomial splines 174Ч190
Hille, E 134
Holladay, J.C. 3 8 46 75 77 73 80
Integral equations 57Ч61 230Ч232
Integration see УNumerical integrationФ
Irregular regions 254Ч258
Kalaba, R.E. 56
Limits on convergence 95Ч96 174 211Ч212
Linear functional 6Ч7 103Ч107 185Ч189 220Ч233 275Ч276
Lynch, R.E. 4 6 7
Mathematical spline 1 9
Meir, A 4 27
Mesh bases 101Ч103 179Ч182
Mesh restrictions 22 25 94Ч95
Method of cardinal splines see УCardinal splinesФ
Minimum curvature property 2 3
Minimum norm property 3
Minimum norm property for cubic splines 75Ч77
Minimum norm property for doubly cubic splines 242Ч243
Minimum norm property for generalized splines 195Ч196 271Ч272
Minimum norm property for polynomial splines 156Ч157
Modified type k 170 (see also УType kФ)
Multidimensional splines 5 6
Nilson, E.N. 2 3 5 7 70 78 136 140 142 237
Nonlinear differential equations 56
Numerical differentiation 42Ч57
Numerical integration 42Ч50 145Ч146 224Ч228
Order of a spline 191
Orthogonality, cubic splines 97Ч101
Orthogonality, generalized splines 213Ч219
Orthogonality, polynomial splines 174Ч179 (see also УCanonical mesh basesФ)
Parametric splines 51 254Ч258
Parametric splines, surfaces 258Ч262
Partial differential equations, numerical solution of 251Ч254 276
Partial splines 237Ч239 273
Peano kernel 6 103Ч105 182Ч189 220Ч224
Peano, G 105 185
Periodic splines 10 148Ч152 156 167 194 236
Polynomial splines 109Ч189
Polynomial splines, best approximation property 157Ч159
Polynomial splines, canonical mesh bases 179Ч182
Polynomial splines, convergence 135Ч143 148Ч152 166Ч174
Polynomial splines, convergence m norm 176Ч179
Polynomial splines, deficiency of 123 143Ч148 157 163Ч164
Polynomial splines, defining values 175
Polynomial splines, degree of 109
Polynomial splines, end conditions 122Ч123 158
Polynomial splines, equal intervals 124Ч135 148Ч152
Polynomial splines, equations for 109Ч123 160Ч165
Polynomial splines, even degree 109Ч110 153
Polynomial splines, existence of 132Ч135 165Ч166
Polynomial splines, first integral relation 155Ч156
Polynomial splines, fundamental identity 154Ч155
Polynomial splines, Hilbert space theory 174Ч189
Polynomial splines, limits on convergence 174
Polynomial splines, linear functional 185Ч189
Polynomial splines, minimum norm property 156Ч157
Polynomial splines, modified type k 170
Polynomial splines, numerical integration 145Ч146
Polynomial splines, odd degree 5 153Ч189
Polynomial splines, orthogonality 174Ч179
Polynomial splines, Peano kernels 182Ч189
Polynomial splines, periodic splines 148Ч152 156 167
Polynomial splines, quintic splines 143Ч148
Polynomial splines, remainder formulas 185Ч139
Polynomial splines, second integral relation 168Ч170
Polynomial splines, simple splines 113
Polynomial splines, type I 113
Polynomial splines, type I' 113
Polynomial splines, type II 113
Polynomial splines, type II' 113
Polynomial splines, type k 167Ч168
Polynomial splines, uniform mesh 148Ч152
Polynomial splines, uniqueness 159Ч160
Qmntic splines 143Ч148
Quadrature see УNumerical integrationФ
Remainder formulas 303Ч105 185Ч189 221Ч228
Sard, A. 6 105 185 222 227 233 275
Schoenberg, I.J. 2 4 5 6 7 44 75 106 185
Schweikert, D.G. 6
Second integral relation 5
Second integral relation for cubic splines 89Ч91
Second integral relation for double cubic splines 248
Second integral relation for generalised splines 204Ч206
Second integral relation for polynomial splines 168Ч170
Secrest, D. 8
Sharma, A. 4 27
Simple splines 7 78 113 194 235
Sokolnikoff, I.S. 2 3 77
Space technology 107Ч108
Spline equations for cubic splines 10Ч16 84Ч87
Spline equations for generalized splines 197Ч199
Spline equations for polynomial splines 109Ч123 160Ч165
Spline surfaces 256Ч262 (see also УCoons surfacesФ)
Spline-on-spline 44 48Ч50
Splines in tension 6
Splines of even degree 109Ч110 153
Splines of odd degree 153Ч389 (see also УPolynomial splines cubic
Strong interpolation 270
Surfaces see УSpline surfacesФ УCoons
Two-dimensional splines, doubly cubic splines 235Ч264
Two-dimensional splines, generalized splines 265Ч276
Type I 75 113 193Ч194 235Ч236
Type I' 75 113 193Ч154 236
Type II 75 113 193Ч194 236
Type II' 75 113 193Ч194 236
Type k 167Ч168 170 194
Uniform mesh 148Ч152 (see also УEqual intervalsФ)
Uniqueness of cubic splines 16Ч19 82Ч83
Uniqueness of doubly cubic splines 239 243Ч244
Uniqueness of generalized splines 196Ч197 271Ч272
Uniqueness of polynomial splines 159Ч160
Uniqueness property 272
Walsh; J.L. 2 3 4 5 6 7 78 136 140 142 237
Weinberger, H.F. 7Ч8
Whitney, A. 2
Ziegler, Z. 5 136
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



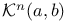 , definition of
, definition of 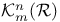 , definition of
, definition of 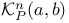 , definition of
, definition of