|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Seligman G.B. — Constructions of Lie Algebras and Their Modules |
|
|
 |
| Предметный указатель |
 = k-th even Clifford algebra 27 = k-th even Clifford algebra 27
 -admissible modules 3 24 39 50 -admissible modules 3 24 39 50
Absolutely irreducible modules 181
Allison algebras 121 136
Allison algebras from non-simple cubic Jordan algebras 136
Allison-Faulkner constructions 140
Benkart’s coordinatizations 180
Cartan multiplication 4 19 38
Clifford algebra 52
Constructions of exceptional Jordan division algebras (Tits) 179
Division Allison algebra 125
Exceptional Lie algebras of relative, rank 1, type 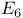 , 79 87 105 , 79 87 105
Exceptional Lie algebras of relative, rank 1, type 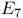 , 82 88 103 , 82 88 103
Exceptional Lie algebras of relative, rank 1, type 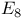 77 86 101 77 86 101
Exceptional Lie algebras of relative, rank 1, type 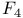 , 77 85 86 99 , 77 85 86 99
Exceptional Lie algebras of relative, rank 2, type 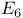 73 90 107 73 90 107
Exceptional Lie algebras of relative, rank 2, type 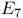 75 89 108 75 89 108
Exceptional Lie algebras of relative, rank 2, type 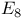 69 91 110 69 91 110
Forms, hermitian and anti-hermitian 21
Freudenthal triple systems 115
Fundamental weights 50 92
Galois-theoretic methods 181—183
Highest weight spaces 2
Homogeneous case of Allison algebras from special Jordan algebras 147 154
Ideals in symmetric powers (Saltman) 11
Involution 21
Involution in Clifford algebra 53
Involution of first/second kinds 21
Involution of orthogonal/symplectic type 21
Irreducible modules for classical algebras, algebras of inner type A 9
Irreducible modules for classical algebras, algebras of outer type A 35
Irreducible modules for classical algebras, algebras of type B 36
Irreducible modules for classical algebras, algebras of type C 33
Irreducible modules for classical algebras, algebras of type D 34 36 172
Kantor algebras 115 121
| Koecher — Tits construction 179
McCrimmon’s theorem on cubic composition algebras 127 128
Minimum condition on inner Ideals 180
Modules for [AA], A central simple 9
Non-homogeneous case of Allison algebras from special Jordan algebras 152 154
Pflster’s examples of quadratic forms 97 98
Quadratic forms giving rise to exceptional algebras 96—98
Rationality of all irreducible modules 184 185
Reductive dual pairs 83
Sl(n,D) 1
Special cubic Jordan algebras and associated Allison algebras 137 144
Splitting, Allison algebras 157 ff
Splitting, exceptional algebras from quadratic forms 85 ff
Splitting, involutorial algebras 29 ff
Splitting, irreducible modules 19
Splitting, ordering of roots 18
Splitting, Sl(l,A) 6
Splitting, super-exceptional Lie algebras 159 ff
Strongly degenerate Lie algebras 180
Super-exceptional rank 1 algebras 141
Super-exceptional rank 1 algebras, Non-existence of 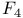 ’s 151 166 ’s 151 166
Super-exceptional rank 1 algebras, type 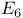 161—162 161—162
Super-exceptional rank 1 algebras, type 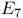 162—164 162—164
Super-exceptional rank 1 algebras, type 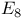 164—166 164—166
Super-exceptional rank 1 algebras, type D 159—-160
Symmetric identities 5
Symmetric powers 5
System of roots of algebra of skew elements 22 23
Tensor products of spin and tensor modules 60
Tensor products of spin modules 58
Test-triples 63
Trilinear identities for Sl(2)-modules 117—118
Trilinear identities for spin modules 63—65
Triple tensor products of Sl(2)-modules 116
Zelmanov’s theorem 181
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 = k-th even Clifford algebra
= k-th even Clifford algebra  -admissible modules
-admissible modules 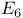 ,
, 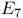 ,
, 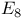
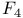 ,
,