Авторизация
Поиск по указателям
Ash C.J., Knight J., Sevenster A. (Ed) — Computable Structures and the Hyperarithmetical Hierarchy
Обсудите книгу на научном форуме Нашли опечатку?
Название: Computable Structures and the Hyperarithmetical HierarchyАвторы: Ash C.J., Knight J., Sevenster A. (Ed)Аннотация: This book describes a program of research in computable structure theory. The goal is to find definability conditions corresponding to bounds on complexity which persist under isomorphism. The results apply to familiar kinds of structures (groups, fields, vector spaces, linear orderings Boolean algebras, Abelian p-groups, models of arithmetic). There are many interesting results already, but there are also many natural questions still to be answered. The book is self-contained in that it includes necessary background material from recursion theory (ordinal notations, the hyperarithmetical hierarchy) and model theory (infinitary formulas, consistency properties).
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: 1st editionГод издания: 2000Количество страниц: 366Добавлена в каталог: 13.05.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Recursion Theorem, application 67 Recursive function, partial 4 Recursive function, total 4 Recursive relation 4 Recursive saturation 295 Recursively enumerable 4 Reducibility, many-one 17 Reduct 38 Relation, arithmetical on numbers and functions 76 Relation, computable 3 Relation, intrinsically 189 Relation, intrinsically 239 Relation, intrinsically c.e. 192 239 Relation, intrinsically computable 185—187 Relation, intrinsically d-c.e. 189 Relation, relatively 165 Relation, relatively intrinsically 192 Relation, relatively intrinsically 165 Relation, relatively intrinsically 178 Relation, relatively intrinsically 165 Relation, relatively intrinsically a-c.e. 168 Relation, relatively intrinsically computable 185 Relation, relatively intrinsically d-c.e. 189 Relation, semi-computable 3 Relational structure 37 210 Relations, intrinsically computably separable 192 Relatively 175 Relatively 177 Relatively intrinsically 253 Relativization of a theorem 15 Remmel 151 Rep(T) 292—294 296 297 309 Rep(T), enumeration of 294 309 Representable set 292 Resplendence 46 Ressayre 127 Rigid 100 198 Rigid, almost 100 263 264 Rogers vi 5 71 Rogers, L. 140 Rosenstein 314 rosser 292 Run of tree with instruction function 215 Run of trees, with instruction function 215 228 s - m - n Theorem 12—14 18 s - m - n Theorem, relativized 16 Satisfaction of predicate formula 37 Satisfaction of propositional formula 34 Satisfaction predicate 52 110 Saturated 46 155 Saturated model 47 Saturation 45 47 127 Schmerl 297 Scott 96 98 99 101 291 292 321 Scott family 96 97 99 174 199 269 291 Scott family, 179 269 273 Scott family, examples 100 Scott family, formally 199 Scott family, formally 175 Scott family, formally c.e. 174 175 197—202 205—208 269 Scott Isomorphism Theorem 96 Scott rank 98 Scott sentence 96 97 Scott set 291—293 Scott set of a model 293 Scott set, appropriate for theory 297 300 302 305 308 Scott set, uncountable 294 Scott Theorem, Isomorphism vi 101 Seetapun 147 Selivanov 143 150 289 Semi-characteristic function 3 Semi-computable 4 Sentence 35 Sentence in infinitary logic 93 Sentence, propositional 34 Separable 260 Separator 12 53 192 319 Separator for a pair of relations 169 Separator, 253 262 Separator, computable 193 Shoenfield 214 Shore viii 206 Shuffle sum of orderings 145 250 251 282 283 315 Single — Valuedness Theorem 84 124 Skolem 84 Slaman 152 160 214 Slinko 206 Smullyan 94 Soare 50 152 309 Solovay 54 291 296 307 308 Special 236 Special ( 303 Special ( 236 302 Spector 62 65 82 129 Stable 239 263 264 Stable computably 197 198 203—205 208 209 239 263 Stable relatively 264 Stable relatively computably 197 206 Standard system 293 Stone Representation Theorem 316 Strongly minimal 312 313 Structure for predicate language 36 Structure representing Scott set 296 300 Structure, cardinality of 36 Structure, computable vii Structure, constructivizable viii Structure, decidable vii Structure, empty 36 Structure, interpretation function of 36 Structure, strongly constructivizable viii Structure, universe of 36 Subformula 34 Subformula of infinitary formula 92 Substructure 38 Sum of orderings 59 314 315 Sum of orderings, infinite 315 Sum of ordinals 59 60 Symbol, constant 34 Symbol, logical 33 34 Symbol, non-logical 33 34 Symbol, operation, or function 34 Symbol, relation, or predicate 34 Symmetric difference 55 TA 51 54 291 292 295 306 307 TA, nonstandard model of 291 296 307 309 Tarski 38 313 320 Tarski Criterion for elementary substructure 38 Tennenbaum 53 294 Term 34 Theory 39 Theory of a structure 51 Theory, complete 39 Theory, completion of 39 Thurber viii 151 281 282 284 Transcendence degree 312 Transfer theorem 143 144 Transfinite induction on ordinal notation 67 Transfinite induction, proof by 58 Transfinite number 58 Transfinite recursion on ordinal notation, computable 67 Transfinite recursion, definition by 59 Transitive set 58 TREE 30 Tree, path through 30 Tree, subtree of 30 Trivial structure 54 128 171 Truth and Forcing Lemma 164—166 Truth of a predicate sentence 37 Truth of propositional formula 34 Turing 4 Turing degree 21 Turing machine 4—6 8 12—15 Turing machine, index for 6 Turing machine, self-replicating 14 Turing machine, universal 4 6 Turing, degree 16 Turing, equivalence 16 Turing, reducibility 16 Type 0 object 23 Type 1 77 Type 1 object 23 Type, complete 46—48 155—157 291 295 Type, complete 297—299 301 302 304 307 Type, complete 291 297 300 301 303 Type, complete 178 309 Type, principal 47 48 Type, realized 46 Ulm 317 Ulm sequence 132 140 141 317 Uniformly computable sequence of structures 279—281 Uniformly computable sequence of structures, coding a set 275 Vandenberg viii Variable bound 35 Variable free 35 Variable free in infinitary formula 92 Variable individual 34 Vaught 151 Vector space vii 33 37 45 90 100 137 160 166 170 173 177 185—187 194 195 242 243 311 312 Vector space, language of 36 Vector space, theory of 311 Ventsov 176 Vlach viii Watnik 144 218 219 284 287 Wehner 152 153 155 Well ordering vii 57—59 61 63 64 91 129 142 239 244 245 263 268 314 Well ordering, computable 61 63 65 129 268 Well ordering, hyperarithmetical 129 X-computable infinitary formula 118 Yang 214
Реклама
-c.e.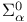 
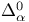
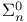
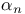-system 
|
|
О проекте