|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Levine J.P. — Algebraic Structure of Knot Modules |
|
|
 |
| Предметный указатель |
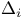 see “Finite modules” “Product see “Finite modules” “Product
 -pairing 48 -pairing 48
 -only torsion 22 -only torsion 22
 -primary sequence 20 -primary sequence 20
Alexander module v
Blanchfield pairing 48
Classification see “Elementary modules” “Product “Rational “Z-torsion
Crowell condition on  97 97
Dedekind  , criteria in low degrees 95 , criteria in low degrees 95
Dedekind  , criterion, general 91 3 , criterion, general 91 3
Dedekind  , definition 20 , definition 20
Derived module 1
Derived sequences 2
Duality in derived sequences, finite case 4
Elementary modules, classification 36
Elementary modules, definition 33
Elementary modules, realization 34
Finite case, classification of 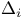 17 17
Finite case, induced product on 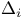 11 11
Finite case, realization 12
Finite modules, 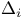 8 (see also “Product structures”) 8 (see also “Product structures”)
Finite modules, duality 4
Finite modules, realization 6
| Global fields, hermitian forms 80
Global fields, integral non-singular  -forms 81 -forms 81
Half-unit 54
Homogeneous modules 32 (see also Product structures)
Ideal class group 96
Ideal Class group, quadratic symmetric case 98
Product Structure,  -pairing 48 -pairing 48
Rational case, classification 76
Rational case, classification of 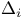 over global field 80 over global field 80
Rational case, realization 77
Rational Module 19 (also see “Product structures”)
Realization theorems see “Elementary modules” “Finite “Homogeneous “Product “Z-torsion
Semi-homogeneous modules, example of non-semi-homogeneous 71
Semi-homogeneous modules, orthogonal decomposition 69
Semi-homogeneous modules, uniqueness of components 6 8
Type k 21
Workable  50 50
Z-torsion free case, classification 54
Z-torsion free case, induced product on 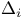 53 53
Z-torsion free case, realization for homogeneous 59
Z-torsion free modules also see “Elementary modules” “Homogeneous “ “ “Product “Semi-homogeneous “Type
Z-torsion free modules, classification in degree < 3 40
Z-torsion free modules, failure of classification in degree > 3 46
Z-torsion free modules, realization 23
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



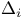
 -pairing
-pairing  -only torsion
-only torsion