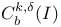|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Chueshov I. — Monotone Random Systems: Theory and Applications |
|
|
 |
| Предметный указатель |
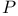 -complete -complete  -algebra 19 -algebra 19
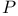 -completion of -completion of  -algebra 21 -algebra 21
 -ergodic measure 51 -ergodic measure 51
 -invariant measure 51 -invariant measure 51
Almost equilibrium 112
Bernoulli shifts 11
Binary biochemical model, random 17 30 58 62 94 97 102 110 114
Binary biochemical model, stochastic 72—74 79 94
Biochemical control circuit 2
Biochemical control circuit, random 171
Biochemical control circuit, stochastic 219
Borel  -algebra 9 -algebra 9
Chapman — Kolmogorov equation 53
Cocycle 13
Comparison principle 109
Comparison principle, random 150
Comparison principle, stochastic 192
Competition and migration model 181
Cone, minihedral 87
Cone, normal 86
Cone, part of 84 91
Cone, regular 86
Cone, solid 83
Conjugacy of RDS 18
Cooperativity condition 147
Disintegration 51
Equilibrium 38
Equilibrium, stable, from above 107
Equilibrium, stable, from below 107
Equilibrium, stable, in probability 211
Equivalence of RDS 18
Fokker — Plank equation 204
Function, cooperative 147
Furstenberg — Khasminskii formula 75
Future  -algebra 52 -algebra 52
Gonorrhea model 175 221
Gross-substitute system 178
interval 83
Interval, absorbing 108
Invariant measure 51
Irreducible matrix 147
Ito stochastic equation 71
Ito stochastic integral 67
Ito’s formula 69
Kick model 16 27 31 38 93
Lattice model 223
Liouville’s equation 58 73
Lyapunov exponent 60 75
Mapping, strongly positive 144
Mapping, sublinear 161 214
Mapping, weakly positive 144
Markov chain 15
Markov family 53
Markov measure 53
Martingale 67
MDS see “Metric dynamical system”
MDS, ergodic 10
Measurable selection theorem 20
Metric dynamical system 10
Multifunction 18
Orbit see “Trajectory”
Ornstein — Uhlenbeck process 79
Outer normal 61
Part (Birkhoff) metric 84
Past  -algebra 52 -algebra 52
Perfection procedure 14
Polish space 13
Probability space 9
Process, adapted 66
Process, continuous 66
Process, predictable 66
Product  -algebra 9 -algebra 9
Projection theorem 21
Radius of dissipativity 26
Random attractor 41
| Random attractor, weak point 210
Random differential equation 56
Random Dirac measure 51
Random dynamical system 13
RDE see “Random differential equation”
RDS see “Random dynamical system”
RDS, 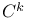 -smooth 14 -smooth 14
RDS, affine 14 46 138
RDS, asymptotically compact 31
RDS, compact 30
RDS, concave 114
RDS, conditionally compact 123
RDS, dissipative 26
RDS, linear 14 45
RDS, order-preserving 93
RDS, s-concave 116
RDS, strictly sublinear 113
RDS, strongly positive 105 145
RDS, strongly sublinear 114
RDS, sublinear 113
Scale function 203 206
SDE see “Stochastic differential equation”
Semi-equilibria 95
Semimartingale 68
Separability set 21
Separable collection of random sets 21
Set,  -invariant 10 -invariant 10
Set, absorbing 26
Set, bounded from, above 84
Set, bounded from, below 84
Set, infimum of 84
Set, invariant 24
Set, invariant, backward 24
Set, invariant, forward 24
Set, lower bound 84
Set, maximal element of 84
Set, minimal element of 84
Set, omega-limit 34
Set, order-bounded 84
Set, random 18
Set, random, bounded 19
Set, random, closed 18
Set, random, compact 19
Set, random, tempered 23
Set, supremum of 84
Set, universally measurable 21
Set, upper bound 84
Skew-product semiflow 15
Spaces  199 199
Spaces 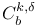 70 70
Spaces 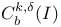 199 199
Speed measure 202 206
Stationary measure 50 53
Stochastic differential equation 70
Stopping time 67
Stratonovich stochastic equation 72
Stratonovich stochastic integral 68
Sub-equilibrium 95
Sub-equilibrium, absorbing 108
Super-equilibrium 95
Super-equilibrium, absorbing 108
Symbiotic interaction 176 222
Tail of trajectory 32
Tempered random variable 23
Top Lyapunov exponent 48 60 75
Trajectory 32
u-norm 84
u-subordination 84
Universal  -algebra 21 -algebra 21
Universe 25
Walras’ law 178
White noise process 12
Wiener process 12 66
Wiener shift 12
Wong — Zaka? type theorem 77
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -complete
-complete  -algebra
-algebra  -ergodic measure
-ergodic measure 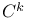 -smooth
-smooth  -invariant
-invariant