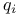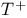|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Gross B.H. — Arithmetic on Elliptic Curves with Complex Multiplication |
|
|
 |
| Предметный указатель |
 37 37
 6 2k 6 2k
 , ,  13 41 13 41
 45 57 60 45 57 60
 4 4
 = ideles of H 23 = ideles of H 23
 58 60 58 60
 , ,  , n(A) 49 78 , n(A) 49 78
 45 47 45 47
 40 60 40 60
 55 72 77 55 72 77
 = Selmer group 53 = Selmer group 53
$T_l(A) 17
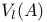 17 20 17 20
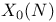 64 66 64 66
 , ,  21 23 57 58 21 23 57 58
 , ,  66 66
 3 26 32 3 26 32
A(P) 1 35 41 67
C , C(i) 73 75 76
C(p) 38
Cl(K) = ideal class-group of K 12
| Complex multiplication 1 12 20
D,  73 74 73 74
Descended curve 1 29
Discriminant  5 67 80 5 67 80
Elliptic curve 4
F=Q(j) field of moduli 1 29 34
H = Hilbert class-field of K 1 29.
h = [H:K] = class-number of K 1 34
Isogeny 6 30 32
K = imaginary quadratic field 1 29 34
L(A/F, s) = L-series of A 19 22 58
Minimal model 14 80
Modular form 64 65 8l
Modular invariant j(A) 1 5 23
Modular parametrization 66
O = ring of integers of K 1 29 34
p, 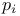 , , 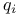 35 40 42 35 40 42
Q-curve 1 32
q-expansion 65 66 81
Q-rank n(A) 49 72
T, 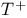 47 48 49 57 47 48 49 57
Tate — Shafarevitch group 53 71
Weieretraas model 4
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте





 ,
, 


 = ideles of H
= ideles of H 
 ,
,  , n(A)
, n(A) 


 = Selmer group
= Selmer group 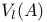
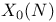
 ,
, 
 ,
, 



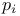 ,
,