|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Lau D. — Function Algebras on Finite Sets |
|
|
 |
| Предметный указатель |
A.I. Mal’tsev’s theorem 268
Adding of certain fictitious variables 94
Adding of fictitious coordinates (rows) 129
Algebra 26
Algebra of finite type 27
Algebra, axiom of 27
Algebra, closed subset 32
Algebra, demiprimal 104
Algebra, demisemiprimal 104
Algebra, directly irreducible 64
Algebra, extension of 31
Algebra, factor 55
Algebra, finite 26
Algebra, finitely axiomatizable 84
Algebra, finitely based 84
Algebra, free 79
Algebra, fundamental operations 26
Algebra, generating system 32
Algebra, hemiprimal 104
Algebra, infinite 26
Algebra, infraprimal 104
Algebra, partial 26
Algebra, preprimal 104
Algebra, primal 104
Algebra, quasiprimal 104
Algebra, quotient 55
Algebra, semiprimal 104
Algebra, set of all subalgebras 33
Algebra, simple 53
Algebra, subalgebra 31
Algebra, type 26 73
Algebra, universal 26
Algebra, universe 26
Algebras of same type 27
All relation 43
All-congruence see “Congruence”
Antiisomorphic 59
Antiisomorphism 59
Arity see “Operation”
Arity congruence 235
atom 112
Atomic proposition 106
Automorphism 52
Automorphism, inner 285
Basis 98
Block 44
Boolean algebra 30
Cartesian product 64
Chain 36
Characterization theorem for Sheffer- functions 215
class 97
Class of algebras, closed 72
Class of all models of  77 77
Class of type 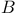 174 174
Class of type 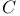 173 173
Class of type 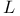 171 171
Class of type 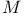 165 165
Class of type 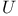 170 170
Class of type  165 165
Class, B-projectable 337
Class, inverse image 337
Class, l-class 280
Class, maximal 98
Class, minimal 589
Class, order 98
Class, submaximal 98
Clone 97
Clone, minimal 590
Clone, strong 599
Closed set system 45
Closure 97
Closure operator 45
Closure operator, algebraic 46
Closure, deductive 82
Co-class 141
Co-clone 127
Co-group 138
Co-monoid 138
complete 98
Completeness criterion for 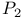 156 156
Completeness criterion for 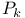 191 191
Completeness criterion for 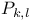 352 352
Completeness criterion for 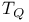 501 501
Completeness criterion for the class of all idempotent functions of 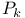 501 501
Completeness problem 117
Completeness theorem for the equational logic 84
Completeness theorem of proportional logic 110
composition 25
Composition, general 129
Conclusion 77
Congruence 52 234
Congruence of the first kind 235
Congruence of the second kind 235
Congruence relation see “Congruence”
Congruence theorem for 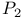 237 237
Congruence, congruence class 55
Congruence, fully invariant 83
Congruence, n-congruence 279
Congruence, theorem for maximal clones 265
Congruence, trivial 53 234
Constant 93
Countability criterion 221
Cyclical exchanging of the lines 127
Deductive closure 82
Depth of a subclass 433
Diagonal 126
Diagonale 43
DIMENSION 291
Direct product 61
Direct product of classes 397
Direct product of functions 397
DNF 99
Domain see “Operation”
Doubling of coordinates (rows) 129
Dual isomorphic 59
Duality principle of the lattice theory 36
Element, central 174
Element, greatest 165
Element, inverse 28
Element, least 165
Element, neutral 28
Elementary operations 95
Embedding 67
Endomorphism 52
equation 76
Equational class 77
Equational theory 77
Equivalence class 43
Equivalence relation 42
Equivalence relation, equivalence class 43
Equivalence relation, finer 351
Equivalence relation, permutable 62
Equivalence relation, transversal to s 556
Equivalence relation, trivial 43
Exchange of the first two rows 127
Factor algebra 55
Factor set 43
Family of sets 65
Fictitious place of a function 93
Field 29
Floor function 331
Free algebra 79
Free generating set 79
Function algebra 30
Function algebra, full 96
Function algebra, iterative full 96
Function, autoduale 167
Function, boolean 93
Function, component 371
Function, components of f 359
| Function, constant 93
Function, extended 600
Function, linear 171
Function, monotone 165
Function, n-ary on A 91
Function, near unanimity function 342
Function, partial 598
Function, preserves the relation  130 130
Function, quasi-linear 171
Function, quasilinear 456
Function, r-th component 168
Function, reducible 150
Function, reduction 599
Function, restricted 600
Function, semiprojection 591
Function, subfunction 598
Function, total 598
Functions,  -congruent 234 -congruent 234
Functions, are associated 238
Functions, identity of 93
Fundamental group 218
Fundamental lemma of Jablonskij 102
Fundamental operations see “Algebra”
Fundamental semigroup 218
Fundamental set 218
Fuzzy logic 116
Galois connection 59
Galois correspondence 59
Generating set 48
Generating system 48 98
Gorlov’s tqheorem 281
Graphic, n-teof A 133
Group 28
Group, abelian 28
Group, additive notation 28
Group, commutative 28
Group, semiregular representation 557
Gruppoid 27
Haddad — Rosenberg theorem 616
Hasse diagram 36
Hilbert-type-calculus 107
Homomorphism 51
Homomorphism theorem for groups 57
Homomorphism theorem for rings 58
Homomorphism theorem, general 55
Homomorphism, kernel 52
Homomorphism, natural 55
Homomorphism, quotient 55
Hull 45 97
Hull system 45
I.A. Mal’tsev’s theorem 241
Ideal 58
Identification of certain variables of f 94
Identification of coordinates 129
Identity 43 76
Inductively set system 68
Information transformer 116
Intersection 127
Inverse element 28
Inverse image, homomorphic 174
Isomorphic 39
Isomorphic lattices 39
Isomorphism 39 52
Isomorphism, anti- 59
Isomorphism, dual 59
Kernel of a group homomorphism 57
Kernel of a homomorphism 52
Kernel of a ring homomorphism 58
Krasner-algebra of first kind 138
Krasner-algebra of second kind 138
Lattice 30
Lattice with 0 and 1 30
Lattice, bounded 30
Lattice, complete 42
Lattice, distributive 30
Lattice, first definition 35
Lattice, isomorphic 39
Lattice, second definition 37
Lattice, sublattice 41
Left unit 241
Lexicographical order 132
Limit class 280
Main theorem of the equational theory, first 81
Main theorem of the equational theory, second 84
Majority function 591
Maltsev-operations 31 95
Mapping, homomorphic 51
Mapping, isomorphic 52
Mapping, order-preserving 39
Mapping, projection- 61
Minority function 591
Module 29
Module, over a unitary ring 29
Module, over the ring  29 29
Module, R-module 29
modus ponens 108
Monoid 28
Neutral element 28
Normal form, disjunctive 99
Normal subgroup 56
Operation symbol 73
Operation, arity 25
Operation, domain 25
Operation, elementary on 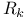 127 127
Operation, n-ary partial 25
Operation, nullary 25
Operation, range 25
Order 98
Order diagram 36
Order, dual 59
Order, partial 36
Partition 44
Peirce decomposition 397
Permutation of coordinates 128
Permutation of variables of f 94
Polymorphism 130
POSET 36
Poset, antiisomorphic 59
Poset, complete 41
Poset, dual isomorphic 59
Post’s theorem 148
Predecessor, proper 292
Predicate 111
Preserve, a relation pair 140
Preserving of a set 97
Preserving of relations 130
Product, cartesian 127
Projection 93
Projection mapping see “Mapping”
Projection onto the 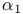 -te, ..., -te, ..., 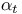 -te coordinates 128 -te coordinates 128
Projection onto the i-th coordinate 127
Proposition 105
Quotient algebra 55
RANGE see “Operation”
Reduct of an algebra 104
Relation algebra on 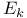 127 127
Relation algebra on 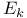 , full 127 , full 127
Relation degree 291
Relation pair 140
Relation pairalgebra, full 141
Relation product 129
Relation set,  -permissible 350 -permissible 350
Relation set,  -independent 179 -independent 179
Relation set, h-regular 178
Relation set, is closed 127
Relation set, minimal coarsening 351
Relation set, permissible 350
Relation,  -derivable 127 499 515 -derivable 127 499 515
Relation, 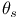 -closed 555 -closed 555
Relation, 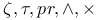 -derivable 128 -derivable 128
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте




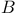
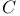
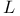
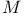
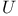

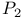
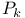
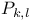
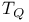

 -congruent
-congruent 
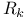
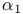 -te, ...,
-te, ..., 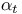 -te coordinates
-te coordinates 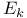
 -permissible
-permissible 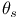 -closed
-closed  -derivable
-derivable