|
Электронная библиотека Попечительского совета механико-математического факультета Московского государственного университета |
| Главная Ex Libris Книги Журналы Статьи Серии Каталог Wanted Загрузка ХудЛит Справка Поиск по индексам Поиск |
© Электронная библиотека попечительского совета мехмата МГУ, 2004-2025 |
|
О проекте |
|
О проекте
|



 -primary component
-primary component 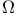
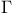 -)
-)