|
Электронная библиотека Попечительского совета механико-математического факультета Московского государственного университета |
| Главная Ex Libris Книги Журналы Статьи Серии Каталог Wanted Загрузка ХудЛит Справка Поиск по индексам Поиск |
|
|
© Электронная библиотека попечительского совета мехмата МГУ, 2004-2026 |
|
О проекте |
|
О проекте
|



![$M[G_k]$](/math_tex/a0d1813058cc389d56c19ae0b2998bbe82.gif)
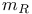
![$V[G_k]$](/math_tex/d34e2c8c8ccf5b8dd80a0f6d64f7a2a582.gif)

 -extension
-extension 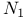 -dense
-dense 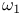 -reflection
-reflection  -Aronszajn tree)
-Aronszajn tree)  -centered
-centered 

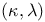 -gap
-gap -generic
-generic ![$L[\mathbb{R}]$](/math_tex/bcffcac9930faed4c29b337c1d67553382.gif) , L[x, z]
, L[x, z] 
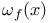 )
)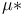
 ”)
”)