|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hobson E.W. — The Theory of Functions of a Real Variable and the Theory of Fourier's Series. Vol. II |

Обсудите книгу на
Нашли опечатку?
Выделите ее мышкой и нажмите Ctrl+Enter
|
Название: The Theory of Functions of a Real Variable and the Theory of Fourier's Series. Vol. II
Автор: Hobson E.W.
Язык: 
Рубрика: Математика/
Статус предметного указателя: Готов указатель с номерами страниц
ed2k:
Издание: Second Edition
Год издания: 1926
Количество страниц: 780
Добавлена в каталог: 17.04.2008
Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
|
|
 |
| Предметный указатель |
Abel 6 11 14 22 34 57 117 175 178
Abel’s lemma 34
Abel’s theorem 175
Abel’s theorem for power-series 175
Abel’s Theorem, converse of 182
Absolute convergence of double series and sequences 52
Absolute convergence of trigonometrical series 548
Absolutely convergent series of numbers 36
Alexandroff 384 676
Anderson 70 76 85
Appell 180
Application of second mean value theorem to Fourier’s series 509
Applications of singular integrals 459
Approach, uniform 108
Approximate representation of functions by trigonometrical series 636
Approximately continuous functions, standard sets of 257
Arithmetic means related to Fourier’s series 557 561 563 587
Arzel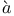 107 118 132 168 293 306 314 659 698 107 118 132 168 293 306 314 659 698
B cher 119 494 498 642 cher 119 494 498 642
Bachmann 7
Baire 137 148 150 264 276
Baire’s classification of functions 276
Baker 498
Banach 755
Bary 678
Bauer 384
Bendixson 306
Bernoulli, D. 477 478 479
Bernstein 551
Bertrand 22 25 29
Besikovitch 697
bessel 482 554
Birkhoff 116
Bolzano 5 402
Bonnet 22 29 510
Borel 69 234 265 643
Brod n 401 539 n 401 539
Bromwich 8 55 69 70 85 181 227 330 351 387 404 471
Brouwer 154
Burkhardt 6 476 478
Cajori 58
Cantor G. 120 399 658 660 674
Cantor’s method of condensation of singularities 399
Carath odory 150 265 489 odory 150 265 489
Carleman 590 600
Catalan 34
Cauchy 6 16 22 24 25 57 64 200 210 289 481
Cauchy-product of series of numbers 56 75
Cell rier 402 rier 402
Cerni 698
Ces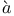 ro 41 66 182 ro 41 66 182
Ces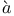 ro sum of series of numbers 41 ro sum of series of numbers 41
Ces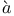 ro’s summation of series 27 47 85 ro’s summation of series 27 47 85
Cesaro summation of divergence 715
Chapman 69 70 73 75 81 85 567
Classes of monotone sequences 157
Complete sequence of normal orthogonal functions 753
Completely integrable sequences 289
Condensation, Cauchy’s test 17
Condensation, Cauchy’s test, of singularities 389
Condition of convergence of series of numbers 1 5
Continuous functions, standard sets of 238
Continuous oscillation of sequences 163
Convergence at a point of trigonometrical series 672
Convergence by segments 132
Convergence of a sequence in a measurable domain 144
Convergence of divergence 705
Convergence of Fourier’s series 491 521
Convergence of monotone sequences 274
Convergence of numerical series in general 34
Convergence of series of normal orthogonal functions 755 762
Convergence of singular integrals 446
Convergence, of sequences on the average 239
Convergence, of series with positive terms 9
Convergence-factors for Fourier’s series 623
Convergence-function 135
Criteria of convergence 15
Cross-neighbourhood 445
Dantscher 214
de la Vall e Poussin’s test for convergence of Fourier’s series 531 e Poussin’s test for convergence of Fourier’s series 531
Dedekind 34
Dell’ Agnola 137 265
Den joy 257
Diagonal sum of double series and sequences 54
Differentiable everywhere-oscillating functions 412
Differentiation and integration of power-series 196
Differentiation of Fourier’s series 639
Differentiation of series 332 335
Dini 14 15 24 26 105 125 337 389 399 402 412 422 510 526 528 659
Dircksen 482
Dirichlet 117 482 493 507
Dirichlet’s conditions 507
Dirichlet’s investigation of Fourier’s series 502
Distribution of points of non-uniform convergence 135
Divergence, of series with positive terms 9
Double Fourier’s series, divergence 698
Double limits 46
Double series and sequences 45
du Bois-Reymond 3 11 15 111 210 224 344 386 402 412 422 497 539 647 659
Duhamel 29
D’Alembert 476 477
Egoroff 145
Egoroff’s theorem 144
Equi-continuous functions 167
Ermakoff 33
Essentially uniform convergence 145
Euler 477 478 479
Extension of functions 154
Extensions of Abel’s theorem for power-series 178
Extensions of Parseval’s theorem 578 591 599
F. Riesz’ classification of summable functions 249
Faber 402 411
Failure of convergence of series of normal orthogonal functions 755
Failure of convergence of singular integrals 456
Falanga 402 407
Fatou 539 548 552 576 631 632 634 635 643 644 697
Fej r 225 498 540 541 559 r 225 498 540 541 559
Fischer 240 577
Ford 67
Formal multiplication of trigonometrical series 585
FOURIER 480 481 494
Fourier transforms 742
Fourier’s repeated integral 725
Fourier’s series, Formal expression of 482
Fourier’s single integral 721
Fr chet 146 chet 146
Frobenius 178
Fubini 335
Functions involving a parameter 141
Functions of bounded variation 702
Functions represented by sequences of continuous functions 185 270 273
Functions, defined by sequences or series 61
Gauss 30
Geiringer 698 704 717
General convergence theorem 422
General convergence theorem for non-summable functions 435
General definition of Fourier’s series 487
General property of sequences 7
Generalization of Riesz — Fischer theorem 599
Generalized integrals 363 371
Generalized second derivatives 664
Genocehi 644
Gibbs 498
Gibbs’ phenomenon 498
Gibson 478
Gronwall 498 541
Gross 717
H lder 66 539 631 659 667 lder 66 539 631 659 667
Haar 540 757 772
hadamard 12 15
| Hahn 67 109 112 125 139 150 152 160 167 282 422 570
Hake 384
Hamack 353 360 639 659
Hancock 214
hankel 389 412
Hardy 43 54 55 56 66 68 69 81 117 130 181 185 227 326 353 360 387 404 533 534 539 552 563 567 570 583 588 598 600 624 635 644 678 697 698 712 722 734 735
Hausdorff 150 152 280 600 676
Heine 656 657
hilbert 56
History of theory of trigonometrical series 480 656
History of theory of uniform convergence 130
Hobson 4 107 125 132 133 137 233 293 314 342 422 460 523 535 545 573 724 763 767 771 772
Holder’s summation of series 66 85
Homogeneous oscillation of sequences 169
Hurwitz 491 576 586
Infinite measure of non-uniform convergence 137
Infinite products, convergence of 58
Ingham 185
Integrable sequences 289
Integrable sequences of continuous functions 312
Integrable sequences of functions that are integrable (R) 312
Integrals containing parameters, limits of 322
Integrals of products, convergence of 464
Integrals, differentiation of 353
Integration of divergence 712
Integration of Fourier’s series 551
Integration of series 289 303
Integration, generalized 363 371
Inversion of order of repeated integrals over infinite domains 344
Ja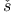 ek 402 ek 402
Jackson, Dunham 234 498
JORDAN 52 341 353 510 522
K pcke 412 pcke 412
K stermann 698 704 711 717 stermann 698 704 711 717
Kaczmarz 768
Kempisty 257
Kneser 494
Knopp 67 70 73 75 87 89 403 407
Kogbetliantz 653
Kohn 33
Kolmogoroff 539 614 626
Krause 698
kronecker 539 658
Kummer 28
Lagrange 200 478
Landau 6 84 179 185 386 460
Laskey 181
Lebesgue 230 234 264 265 270 277 278 282 289 422 438 454 459 469 487 514 528 538 540 561 563 576 586 663 667 675
Lebesgue’s constants 541
Lerch 230 643
Liapounoff 576
Limiting values of Fourier’s coefficients 514
Limits of coefficients of trigonometrical series 659
Liouville 771
Lipschitz 520 528
Littlewood 23 69 181 184 185 539 552 563 570 588 598 600 635 644 678 697
London 46
Looman 384 757
Love 498
Lusin 284 539 549 550 697
M. Riesz’ extension of Parseval’s theorem 610
Maxima and minima of functions of two variables 213
Maxima and minima, of functions of one variable 151
Maximal and minimal functions 102
Measure of non-uniform convergence 133
Menchoff 678 763 767 768
Mercer 87 772
Mertens 57
Method of monotone sequences 374
Michelson 498
Mittag-Leffler 230
Moigno 289
Mono-tonoid functions 703
Monotone sequences associated with a given sequence 159
Monotone sequences, of functions 148
Monotonoid functions 703
Moore, C. N. 70 227 387 698 717
Moore, E. H. 403
More slow convergence 10
Multiplication of power-series 194
Necessity of conditions in the general convergence theorem 438
Neder 490 655
Neumann, C. 510
Newman 257
Non-absolute convergence of double series and sequences 54
Non-convergence of Fourier’s series 539
Non-convergent series of numbers 2
Non-differentiable functions, construction of 389
Non-uniform convergence, points of 109
Order of Fourier’s coefficients 518 538
Oscillation of sequences of integrals 318
Oscillation of singular integrals 456
Osgood 119 120 121 135 137 293 306
Ottolenghi 73
O—o notation 6
PAL 154
Parseval 575
Parseval’s and Riesz — Fischer theorems for normal orthogonal functions 759
Parseval’s theorem 575
Parseval’s theorem for divergence 718
Parseval’s theorem for double series 718
Partial sums of Fourier’s series 489
Paucker 25
Peak and chasm functions 99
Pereno 412
Perron 489
Perron’s definition of integration 382
Picard 230 637 698
Plancherel 742 752 763
Plessner 626 632 696 697
Poincar 498 498
Points of non-uniform convergence 109
Points of simply uniform convergence 112
poisson 481 629
Poisson summation of divergence 717
Poisson’s summation 629
Poisson’s summation for double series 717
Poisson’s summation of Fourier’s series 629
Pollard 577
Pompeiu 401
Power-series 172
Primitives of functions 284
Pringsheim 8 11 16 20 22 25 26 34 46 54 59 64 111 130 694 722 724
Priwaloff 573 656
Properties of Fourier’s coefficients 573
Properties of measurable functions 178 282
Properties of power-series 192
Raabe 29
Radmacher 763
Rajchman 335 587 647 663 677 678 682
Reiff 6 130
Remainder in Taylor’s theorem 200
Remainder of series of numbers 1
Repeated integrals, inversion of order of 338
Restricted Fourier’s series 686
Riemann 38 514 522 645
Riemann’s summation of Fourier’s series 645
Riemann’s theory of trigonometrical series 645
Riesz — Fischer theorem 577
Riesz, F. 240 249 516 577 600 608 762
Riesz, M. 68 85 90 567 611 612 635 659 682 698
Roche 200
Runge 230
Rychlik 402
Sachs 478 545
Sales 335
Scheeffer 213 214 220
Schl fli 497 fli 497
Schl milch 31 200 643 milch 31 200 643
Schnee 67
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



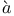
 cher
cher  n
n  lder
lder 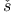 ek
ek  stermann
stermann  fli
fli