|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Buckingham R.A. — Numerical Methods |
|
|
 |
| Предметный указатель |
Interpolation, Lagrangian 71 116 481
Interpolation, Lagrangian coefficients 77
Interpolation, Lagrangian, error of 84
Interpolation, mixed formulas 126
Interpolation, subtabulation 121
Interpolation, with two variables, by differences 482
Irwin, J.O. 498 600
Isaacson, E. 626
Iterative methods 246—284 392 423 464 638
Iterative methods, Aitken’s 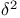 process 258 260 283 393 430 process 258 260 283 393 430
Iterative methods, Bernoulli — Aitken method 277 394
Iterative methods, for elliptic equations 638
Iterative methods, for Fredholm equations 464
Iterative methods, for latent roots of matrices 392
Iterative methods, for linear equations 423
Iterative methods, for quadratic factors 266
Iterative methods, for roots of algebraic equations 246
Iterative methods, general properties 256
Iterative methods, limits of error 432
Iterative methods, order of process 256
Iterative methods, scalar products, use of 395
Jackson, J. 226
Jahnke, P.R.E. xii
Jeffreys (WKB) method 199
Jeffreys, H. 201
Jeffreys, H., and Jeffreys, B, S. xi 158 186 188 192 203 254
John, H.A. 422
Jordan, C. 312 323 572
Jordan, W. 356 357
Kaplan, S.A. 514
Kempner, A.J. 276
Kerawakt, S.M. 323
Kincaid, W, M. 403
Laderman, J. 329
Lagrange multipliers 304
Lagrange, J.L. 71
Lagrangian methods 69—90
Lagrangian methods, cubature 496
Lagrangian methods, differentiation 77 579
Lagrangian methods, interpolation 71 481
Lagrangian methods, quadrature 78 580
Lagrangian methods, step-by-step integration 217
Laguerre polynomials 326
Lanczos, O. 329 356 382 392 411 413 419 432 628
Langer, B.E. 203
Laplace formulas 157
Latent roots and vectors of matrices 371 392 456
Latent roots and vectors of matrices, Bayleigh’s principle 457
Latent roots and vectors of matrices, complex roots 407
Latent roots and vectors of matrices, defective matrices 387 407
Latent roots and vectors of matrices, definitions 371
Latent roots and vectors of matrices, deflation 401
Latent roots and vectors of matrices, deflation, alternatives to 420—421
Latent roots and vectors of matrices, Lanczos’ method 382 411
Latent roots and vectors of matrices, matrix polynomials, use of 403
Latent roots and vectors of matrices, numerical examples 397 402 403 408 410 416 417
Latent roots and vectors of matrices, repeated real roots 407
Latent roots and vectors of matrices, scalar products, use of 383 395
Latent roots and vectors of matrices, symmetric matrices 397
Latent roots and vectors of matrices, symmetry properties 397 530
Latent roots of differential and integral equations 456 526
Latent roots of differential and integral equations, elliptic equations 562
Latent roots of differential and integral equations, Milne’s method 526
Latent roots of differential and integral equations, numerical examples 460 469 473 529
Latent roots of differential and integral equations, Rayleigh’s principle 458
Latent roots of differential and integral equations, relaxation, use of 459
Least squares, method of 298—333
Least squares, method of, continuous approximation 323
Least squares, method of, Legendre’s principle 298
Least squares, method of, normal equations 300 303 331 339
Least squares, method of, orthogonal polynomials, use of 312
Least squares, method of, validity 305
Legendre, A.M. 298 487
Legendre’s principle 298
Lehmer, D.H. 285 293
Leverrier, U.J.J. 418
Levy, H. 174 244
Lewy, H. 514 525
Liebmann, H. 539
Lin, Shi-Nge 272
Linear independence 298
Loud, W.S. 245
Lovitt, W.V. 464
Lowan, A.N. 329 507 577
Lubbock, J.W. 163 165
Lucas 91
Mack, C. 268 270
Maclaurin, C. 157
Madelung’s transformation 195
Margenau, H. 325
Matrix definitions 336 370
Matrix definitions,  -matrix 371 -matrix 371
Matrix definitions, adjoint matrix 358 373
Matrix definitions, characteristic function 371
Matrix definitions, defective matrix 372
Matrix definitions, inverse of matrix 346
Matrix definitions, latent roots and vectors 371
Matrix definitions, norm 432
Matrix definitions, order, rank, degeneracy 336
Matrix definitions, product of matrices 337
Matrix definitions, scalar product 372
Matrix definitions, trace or spur 374
Matrix definitions, transposed matrix 337
Matrix inversion 346 434
Matrix inversion, comparison of methods 349
Matrix inversion, improvement of inverse 360 434
Matrix inversion, symmetrical matrix 346 349
Matrix inversion, triangular matrix 351
Matrix inversion, unsymmetrical matrix 352
Miller, J.C.P. xii 16 29 31 41 126 205
Miller, W.Lash 180
Milne, W.E. xi 164 207 217 235 238 240 274 305 312 327 361 504 519 523 526 532 541 5^5
Milne-Thomson, L.M. xii 93
Mineur, T.O.N. xi
Minimized iterations, method of 357 411
mistakes 12
Mistakes, avoidance of 12
Mistakes, causes of 15
Mistakes, sum checks, use of 358 441
Mitchell, K. 285
Modified differences (“throwback”) 119 484
Moments 61 573
Moments, of ascending and descending factorials 61
Moments, of central factorials 64
Moments, power 61 63 66
Moments, use in fitting data 319
Morris, J. 356 432
Motzkin, T.S. 443
Moulton, F.R. 180
Murphy, G.M. 325
Neville, E.H. 507
Newton — Raphson method 250 262
Newton, Isaac 79 92 95 108 252 254 434
Newton’s divided difference polynomial 95
Nicolson, P. 516.520
Nogrady, H.A. 265
Normal equations 300 303 331 339
Nystrdm, E.J. 224
Olver, F.J.W. 209 217 277 285 292
Orthogonal polynomials 306 325
Orthogonal polynomials, Jacobi 326
Orthogonal polynomials, Legendre, Hermite, Laguerre 325
Orthogonal polynomials, Tchebycheff (Chebyshev) 306 326
O’Brien, G.G. 514
Parabolic equations 514
Parabolic equations, boundary conditions 513
Parabolic equations, definition 511
Parabolic equations, diffusion equation, analytical solution of 520
Parabolic equations, du Fort — Frankel method 518
Parabolic equations, finite difference approximations 515
| Parabolic equations, instability of solution 515
Parabolic equations, numerical example 521
Parabolic equations, relaxation, possible use of 524
Parabolic equations, solution by other methods 523
Partial differential equations see “Differential equations”
Partial differentiation 502
Pearson, Karl 482 484 488 492
Perturbation method 197
Picard, C.E. 176 180
Pollak, L.W. 329
Polynomial equations 264—294
Polynomial equations, cubic 264
Polynomial equations, mechanical root-finding 276
Polynomial equations, methods for solving, Bairstow 274
Polynomial equations, methods for solving, Bernoulli — Aitken 277
Polynomial equations, methods for solving, Brodetsky — Smeal 292
Polynomial equations, methods for solving, Dietzold 394
Polynomial equations, methods for solving, Lin 272
Polynomial equations, methods for solving, Olver 292
Polynomial equations, methods for solving, Porter and Mack 268 271
Polynomial equations, methods for solving, root-squaring 284
Polynomial equations, quadratic factors of 266
Polynomial equations, quartic 268 271
Polynomial equations, sextic 268 296
Polynomial equations, test functions, use of 267 270
Polynomial equations, zeros of power series 293 (see also “Algebraic equations”)
Polynomials 56
Polynomials, curve-fitting, use in 299 312
Polynomials, factorial expansions for 57 58
Polynomials, importance for interpolation 70 481
Polynomials, Lagrange’s polynomial 71 473 481
Polynomials, Newton’s polynomial 96
Polynomials, solution of integral equations 471
Polynomials, sums and differences of 56
Polynomials, tabulation of 59 (see also “Orthogonal polynomials”)
Porter, A. 268 270
Precision of numbers 5
Prony’s method 329
Quadratic factors 266
Quadrature 78 129
Quadrature, by central differences 132
Quadrature, by Euler — Maclaurin series 158*9
Quadrature, by matrix inversion 447
Quadrature, errors 82 85 88 135
Quadrature, estimates, improvement of 89
Quadrature, Gregory’s formula 130 149 165 366
Quadrature, Newton — Cotes formulas 79 580
Quadrature, partial range formulas 83 580
Quadrature, repeated integration 151
Quadrature, Steffensen’s open formulas 82 580
Quadrature, subtraction of singularities 139 (see also “INDEX OF USEFUL FORMULAS”)
Quartic equations 268 271
Raphson, J. 250
Rayleigh’s principle 457
Rees, M. 526
Regular singularity 185
Reiersol, O. 391
Relaxation method 436 449 550
Relaxation method, accuracy of solutions 454
Relaxation method, checking of residuals 441
Relaxation method, for elliptic partial equations 540 550
Relaxation method, for first-order equations 453
Relaxation method, for latent roots 459
Relaxation method, for linear algebraic equations 436
Relaxation method, for linear differential equations 449
Relaxation method, for non-linear equations 455
Relaxation method, for parabolic equations 524
Relaxation method, further applications 561
Relaxation method, Gauss’ transformation 441
Relaxation method, group operations 439
Relaxation method, limitations 443 463
Relaxation method, numerical examples 438 439 443 451 460 552 554
Relaxation method, operations table 438
Relaxation method, over- and under-relaxation 441 541
Relaxation method, “sinking of residuals” 540 551
remainders 574 579
Residuals 359 437 441 444 540
Richardson, L.F. 90 403 539
Robinson, G. xi 106 114 300 329 331
Rolle’s Theorem 84
Root-squaring method 284
RosenhLd, L. xii
Rounding errors 3 18 22 136 215 ?60
Routh, E.J. 246
Sadler, D.H. 16
Salzer, H.E. 91 161 507 577
Samuelson, P.A. 256 379
Sastdy, M. 312 323
Scarborough, J.B. xi
Scheen, W.L. 29
Schiff, L. 203
Seidel, P.L. 423
Severn, R.T. 523 524
Shaw, F.S. 566
Shea, J.D. 312
Sheppard, W.F. 51
Shortley, G.H. 542 550
Significant figures 6
Simpson, T. 79 80
Simpson’s rule 79 80 82 88 90 141 496
Sine integral 191
Smeal, G. 292
Sommerfeld, A. 511
Souihwell, B.V. 423 437 658 563 565
Square roots 40 252
Steffensen, J.F. xi 82 83 86 93 123 158 165 576
Stein, P. 424
Stiefel, E. 356
Stirling numbers 57 58 468—473
Stirling’s interpolation formula 110 134 333 390 483
Stokes, G.G. 191
Stumpff, K. 329
Subtabulation 121
Subtabulation, bridging differences, use of 123
Subtabulation, end-figure process 123
Summation 155
Summation, by Euler — Maclaurin formulas 156 167
Summation, by Lubbock and Woolhouse formulas 163 167
Summation, by parts 167 168
Summation, of alternating series 161
Sums 46 155
Sums, backward (ascending) 47
Sums, central 51
Sums, definite 43 50 156
Sums, forward (descending) 48
Sums, indefinite 47 155
Sums, mean 51
Sums, of factorials 53 54 56
Sums, relations with tabular values 50
Sums, repeated 50 156
Symbolic method 143 480
Symbolic method, central difference and averaging operators 146 480
Symbolic method, displacement and difference operators 143 480
Symbolic method, relations with integral and differential operators 147 481
Symbolic method, summation operators 155
Symbolic method, validity 154
Synthetic division 59 267
Szegd, G. 327
Tables 16
Tables, Barlow xi 14 22
Tables, Chambers [6] xi 21 24 77 108 134
Tables, checking entries 25 31
Tables, construction of normal 18 203
Tables, critical 16
Tables, Interpolation and Allied xii 77 115 120 124 127
Tables, interpolation coefficients (for use with differences) 115
Tables, interpolation in normal 18 76 116
Tables, inverse interpolation 22
Tables, Lagrangian interpolation coefficients 77
Tables, Milne — Thomson 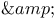 Comrie [4] xii 21 Comrie [4] xii 21
|
|
 |
| Реклама |
 |
|
|
 |
 |
|
 |
|
О проекте
|
|
О проекте



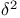 process
process  -matrix
-matrix 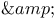 Comrie [4]
Comrie [4]