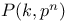|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| R.D.Carmichael — Introduction to the Theory of Groups of Finite Order |
|
|
 |
| Предметный указатель |
 -subgroup 82 83 84 163 -subgroup 82 83 84 163
Abelian groups 30 52 66 69 70 73 83 84 98—119 289—322
Abstract groups 31—36 166—187
Abstractly identical fields 250 251 260
Abstractly identical groups 33
Additive group 243 245
Adjoint configurations 435
Algebras A[s] 396
Algebras of doubly transitive groups 395—414
Alternating group of degree 4 34—36 42 64 65
Alternating groups 20 21 31 38 153 169 172 176 185
Analytical representations 108 263 289 295
Array, rectangular 44
Associated configurations 415
Associative law 6 16
Belonging to a field 246
Belonging to a group 21
Blichfeldt, H. F. 64 66 68
Bocher, Maxime 4
Box porism 417
Burnside, W. 197 234 271
Bussey, W. H. 323 327 345
Central 47 66 83 87
Central factor-group 120
Characteristic determinant 192
Characteristic equation 192
Characteristic subgroup 81 83 84
Characteristics 193 210 223
Chief-series 97
Circular permutation 7 14 15
class 3
Co-ordinates in groups 290
Coble, A. B. 417 418
Collineation 359
Collineation group 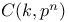 360 362 360 362
Collineation groups 355—394
Combination, rules of 4
Commutative 13 27
Commutative group 30
Commutator subgroup 29 36 37 38 39 53 82 88 127
Commutator-series 97
Commutators 13 14 28 37 39 41 42 53 70 73
Complementary configurations 415
Complete 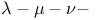 configurations 433 437 configurations 433 437
Complete 2-2-k-configurations 42 434 437
Complete conjugate set 47 71
Complete groups 81 83 95 96
Completely reduced form 208
Completely reduced sets 200
Completely reducible 200
Composite group 48 69 71 226
Composition of groups 204 206
Composition-factor-groups 89
Composition-factors 89
Composition-series 88 96 97
Compound of two groups 204 205 206
configurations 346 415—441
Conformal groups 32 38 41 53 70 71
Congruent polynomials 252
Conjoint groups 57
Conjugate elements 46
Conjugate subgroups 47
Conjugate-imaginary groups 191 198
Conjugate-imaginary transformations 191
CYCLE 11
Cyclic groups 29 36 38 52 83 104
Cyclic permutation 7
Defining relations 34 166—187
Definite Hermitian form 196
Degree 5 19
Degree of transitivity 139 148
Derived groups 29
Desargues 337
Dickson, L. E. 64 66 68 285 315 396 403 404 413
Dicyclic groups 182 183
Dihedral groups 181 183
Direct product 52
Double holomorph 81
Double modulus 252
Doubly transitive groups 266 267 272 286 305 306 310 313 319 320 337 363 372 375 395—414
Doubly transitive groups of degree n and order n(n— 1) 143—147
Duality, principle of 330 334 337
Element 3
Elements of a group 26—28
Emch, A. 440
Empirical theorems 315—317
Equality 16
Equivalent representations 207
Euclidean geometries 329
Even permutation 9 10 19 20
Factor-groups 84—88
Fields 242—288
Fields within a field 260
Finite fields 242—288
Finite geometries 323—354 407—413
Finite group 17
Frobenius, theorem of 92 126
Fundamental theorems 44 55 58 66 68
Galois field defined 255
Galois fields 242—288
Galois fields, existence of 256
General isomorphism 74 75 85
General linear homogeneous group 291
Generators 30 31 66 82
Geometric set of subgroups 291 328 344
Geometries, finite 323—354 407 408
Group characteristics 210 223
Group of degree 11 and order 660 24 25 65
Group of degree 7 and order 168 21—22 24 25 31 53 65 84
Group of inner isomorphisms 78 87
Group of isomorphisms 78 83 84 95 289—322
Group of order 4n + 2 94
Group property 16
Group, definition of 15—19 395
Groups of degree 13 40 72
Groups of degree 15 43 162 165
Groups of degree 16 42 43 165
Groups of degree 4 151
Groups of degree 5 151
Groups of linear transformations 188—241
Groups of order 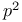 65 69 65 69
Groups of order 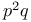 70 70
Groups of order 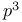 69 71 73 69 71 73
Groups of order 60 72
Groups of order 6p 72
Groups of order 8 36 37 38 94 134
Groups of order p(p - 1) 40 41 42
Groups of order pq 64 95
Groups of orders 1-15 69
Groups of orders 16-26 73
Groups of prime degree 234 239 387 389
Groups of prime order 45
Groups {s, t} such that 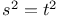 177 177
Hamiltonian groups 113—116 117
Hermitian forms 196
Hilton, H. 113
Holomorph 79—81 83 84 163 303
Identical element 16
Identical isomorphism 76
Identical permutation 5
Identical representation 207
Identity 16 17 190 395
Imprimitive groups 159
Imprimitive systems 160
Index of subgroup 45
Infinite group 17
Inner isomorphism 78 87
Integral elements of ![$A[{p}^{n}]$](/math_tex/c399d5157e904f377dcf5a63fb5ecd0382.gif) 404 404
Integral marks 244 261
Intransitive groups 54 158 162
| Invariance under group 20 21
Invariant 46 47
Inverse 6 16 189 396
Irreducible components 208
Irreducible equation 246
Irreducible groups 200
Irreducible in a field 246
Irreducible modulo p 253
Irreducible representations 207
Isomorphism 31 74
Isomorphism of algebras 402
Isomorphism, general 74 75 85
Isomorphisms of a group with itself 76—79
Isomorphisms of Abelian groups 107—113 289—322
Isomorphisms of cyclic groups 104
Jordan, C. 146
Kronecker, L. 229
Lagrange 44
Linear fractional groups in one variable 266
Linear groups in one variable 265
Linear homogeneous group 111
Linear nonhomogeneous group 111
Linear transformations in A[s] 400
Magic squares 393
marks 242 396
Mathematical system 4
Mathieu groups 151 165 263 283 288 431
Matrix of substitution 188
Maximal self-conjugate subgroup 82
Maximal subgroup 82
Maximum self-conjugate subgroup 82
Maximum subgroup 82
Metacyclic groups 184
Miller, G. A. 64 66 68 150 433
Modulus double 252
Monomial transformation 193
Multiple isomorphism 75
Multiple transitivity 139 143
Multiplication 6 16 189
Multiplication (transformation) 193
Multiplication table 32
Multiplicative group 243 248
Multiplier 192 193
Multiply transitive groups 143 387 389 392 441
Netto, E. 425 433
Non-Abelian group 30
Noncommutative group 30
Noncyclic group 29
Nonequivalent representations 207
Nonzero definite 198
normal 46 47
Normalizer of element 49
Normalizer of subgroup 49
Not-square marks 262
Object, mathematical 3
Octic group 20 24 30 31 36 37 54 176 373
Odd permutation 9 19
Order 10 11 17 27
Order of a field 243
Order of a mark 247
Outer isomorphism 78
Pappus 339
Partitions of a group 84
Perfect group 29 38 94
Permutable 13 27
Permutation groups 19 22—23 138—165
permutations 5
Post-multiplication 56
Power 10 11 14 26 27
Pre-multiplication 56
Prime-power groups 30 67 69 73 120—137
Primitive groups 159 162 163 165 372 375
Primitive groups of degree 8 165
Primitive groups off low degree 392
Primitive mark 248 250 288
PRODUCT 5 16 189
Projective geometries 323
Projective group 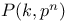 355 355
Projective transformations 355
Proper subgroup 28
Punct 331
Quadrangle 341
Quadruple systems 25 26 72 73 429 436 440
Quadruples 348 351 352 353 354
Quadruply transitive groups 389 see
Quaternion group 113 117
Quintuple systems 432
Quintuples 354
Quintuply transitive groups see “Mathieu groups”
Quotient 85
Quotient group 85
Rect 331
rectangular array 44
Reduced sets 200
Reducible groups 200
Reducible modulo p 253
Regular groups 54 55 217
Regular permutations 11 39
Representation as a regular group 53
Representation as a transitive group 155
Representation of a finite group 206
Representations of permutations 263
Roots of unity 228 287
Rules of combination 4
Schur, I. 234
Self-adjoint configurations 436
Self-conjugate 46 47
Sextuple systems 431
Similar permutations 12 14
Similarity transformation 193
Simple groups 48 64 71 83 276—283 285
Simple groups of order less than 1, 000, 000 285
Simple isomorphism 31
Simply isomorphic 75
Soluble group 91
Solvable group 91 92 94 97 229
Square marks 262
Standard form of permutation 11
Subalgebra 404
Subfield 260
Subgeometries 334 419
Subgroups 28—29 44 81—83
Subgroups of index 2 52
Subgroups of prime-power order 63
Substitution polynomial 264
Substitutions 5 188
Sylow subgroups 58 63 64 65 66
Sylow's theorem 58
Symmetric group 19 21 24 31 38 154 169—176
Symmetric group of degree 4 64 65
Symmetric group of degree 6 43
Symmetric group of degree n 65
system 3 4
Systems of imprimitivity 160
Tactical configurations 346 415—441
Theorem of Desargues 337
transform 12 13 27 28 47
Transformations, linear 188
Transitive group, representation as 155
Transitive groups 54 139 152 162 163 164 165 229 234 239
Transitive sets 158
Transitivity, degree of 139 148
Transposed transformation 191
Transposition 7
Triple groups 425
Triple systems 21 53 425 436 440 441
Triply transitive groups 147—148 267 272 286 305 306 320 363 372 375 389 413
Type of abelian group 67 98
Veblen, O. 323 327 339 340 345 360 394 407
Weber, H. 236
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -subgroup
-subgroup 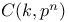
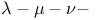 configurations
configurations 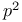
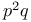
![$A[{p}^{n}]$](/math_tex/c399d5157e904f377dcf5a63fb5ecd0382.gif)