|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| S.S.Gelbart, S.Rallis, I.Piatetski-Shapiro — Explicit Constructions of Automorphic L-Functions |
|
|
 |
| Предметный указатель |
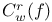 , , 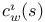 24 24
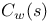 23 23
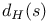 29 29
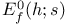 21 21
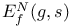 135 135
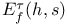 60 60
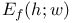 3 3
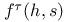 60 60
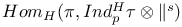 105 105
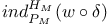 3 3
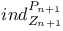 104 104
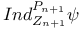 109 109
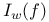 23 23
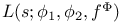 12 12
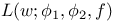 3 3
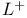 , , 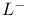 8 8
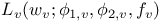 5 5
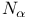 , , 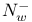 20 20
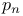 58 58
 60 60
 102 102
 101 101
 102 102
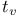 53 53
 72 72
 101 101
 105 105
 105 105
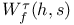 61 61
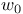 28 28
 60 60
![$[a,b]_{\mathbb{Z}}$](/math_tex/240a09a190313a55259da9d3a9ef434d82.gif) 24 24
 67 67
 99 99
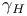 38 38
 , ,  8 8
 21 21
 61 61
 21 21
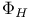 , ,  19 19
 22 22
 72 72
 103 103
 59 59
 87 87
 99 99
 95 95
 53 53
Anti-symmetric square representation 134
Asymptotic expansions 125—126
Basic identity 3 59 50 63 66
Bernstein — Zelevinsky theory 101
Bernstein's theory 126
Combinatorial lemma 31
Cuspidal data 107
Derivative of a representation 103
Doubling variables technique 7 16
Eisenstein series E(h, s) 3 60 63 65
Euler product expansions 93
Fourier expansion of 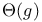 65 65
Fourier expansion of a cusp form 59 61
Gindikin — Karpelevich method 23
Global zeta-integral I(s,  , E) 60 62 65 , E) 60 62 65
Godement — Jacquet construction 10
I(s,  , E) 60 , E) 60
| Intertwining operators 22 100
Jacquet functor, modified 102
Jacquet functor, ordinary 102
Jacquet module 105
Jordan — Holder series 106
k-th derivative of  103 103
Kato formula 139
Kirillov model 126
L(2s',  , ,  ) 134 ) 134
L(s, 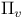 , r) 53 , r) 53
L(s,  , , 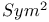 ) 135 ) 135
L(s,  , ,  ) 135 ) 135
Langlands' conjecture 53
Langlands' theory of Eisenstein series 133
Levi decomposition 68
Lifting problem 54
Local coefficients of Shahidi 135
Local factors for GL(n) 34 36
Local factors for O(2n) and Sp(2n) 36 45
Local functional equation 99
Local Langlands factor 53
M(s) 99
Main orbit 2
Maximal parabolic subgroup 68
Metaplectic group, global 86
Metaplectic group, local 86
Method A 59
Method B 62
Method C 64
MP 86
Negligible orbits 2 4 15 115
Non-degenerate character 73 82
Normalized Eisenstein series 135
Ordinary induction 109
Orthogonal groups 11
P* 77
Poincare polynomials 138
Quaternionic hermitian group 14
R(G) 87
Rankin — Selberg method 54 97
Rankin — Selberg type L-functions 3
Shimura type zeta-integral 91
Shimura's method 91
Simple roots for SO(2n + 1) or SO(2n) 73
Simple roots for Sp(2n) 88
Small representation 118
SO(2n) 69
SO(V) 67
Sp(n), SP(V) 85
Special Eisenstein series 21
Special Orthogonal group 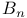 67 67
Spin groups 97
Standard cuspidal subgroup 58
Standard representation of Gelfand — Graev 104
Symplectic group 7 85
Theorem A 60
Theorem B 63
Theorem C 66
Theta-functions 87
Unitary groups 11 97 98
Unramified local zeta integral 137—138
V' 69
Weil representation 87
Whittaker model for  61 93 61 93
X,  67 67
Z( , s, , s, 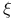 ) 12 ) 12
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



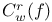 ,
, 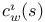
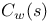
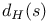
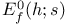
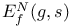
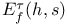
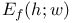
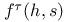
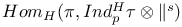
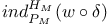
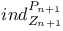
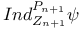
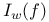
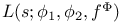
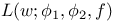
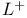 ,
, 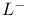
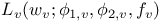
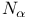 ,
, 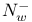
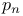




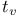




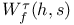
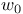

![$[a,b]_{\mathbb{Z}}$](/math_tex/240a09a190313a55259da9d3a9ef434d82.gif)


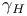
 ,
, 



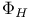 ,
, 








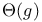
 , E)
, E) 
 ,
,  )
) 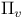 , r)
, r) 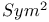 )
)  )
) 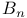


 , s,
, s, 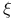 )
)