|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Kanovei V.G., Reeken M. — Nonstandard Analysis: Axiomatically |
|
|
 |
| Предметный указатель |
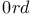 10 24 10 24
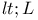 161 161
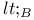 362 380 362 380
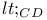 362 380 362 380
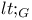 168 168
 151 151
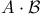 324 324
![$a^{put}[G]$](/math_tex/156c75acc81dce75c2e3f28c86cc8f7282.gif) 261 261
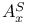 296 296
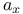 192 192
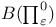 331 331
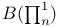 331 331
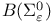 331 331
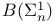 331 331
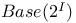 321 321
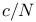 364 364
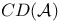 327 327
 321 321
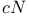 364 364
 143 143
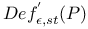 220 220
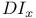 195 195
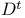 275 275
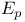 102 102
 48 48
 166 166
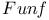 164 164
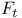 192 192
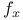 140 140
 258 258
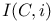 143 143
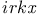 44 44
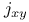 199 202 199 202
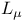 352 352
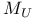 37 378 37 378
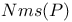 261 261
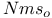 261 261
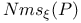 261 261
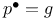 184 184
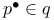 184 184
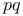 106 106
 275 275
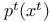 275 275
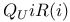 325 325
 42 42
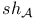 ”X 329 ”X 329
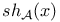 329 329
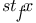 225 225
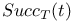 191 191
 190 190
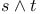 191 191
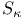 151 151
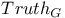 T, modified truth predicate 169 T, modified truth predicate 169
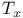 192 192
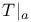 193 193
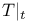 193 193
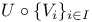 326 326
 141 141
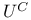 326 326
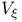 42 42
![$V_{\xi}[U]$](/math_tex/0cb11dc2afd77467890f32a4ed9f231682.gif) 44 44
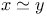 54 54
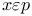 184 184
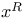 195 195
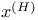 258 258
 33 33
 27 220 27 220
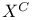 321 321
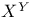 10 10
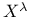 33 33
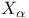 167 167
 193 193
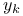 160 160
![$[x]^{a}$](/math_tex/f141c076963767906c37b369109c272b82.gif) 211 211
![$[\Phi]$](/math_tex/a6e30be8d42b03947fb3a75575c9c63a82.gif) 142 142
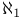 321 321
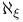 25 25
 202 211 202 211
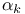 160 160
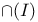 325 325
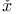 258 258
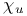 325 325
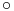 326 326
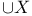 21 21
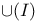 325 325
![$\Delta^{0}_{0}[\mathcal{X}]$](/math_tex/f77c9ea56146cb9926eba836bf19723482.gif) 321 321
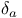 263 263
 141 141
 -isomorphism 132 -isomorphism 132
 —structure 46 132 —structure 46 132
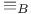 362 380 362 380
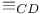 362 380 362 380
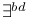 111 111
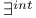 14 14
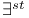 14 14
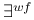 16 16
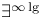 58 58
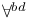 111 111
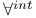 14 14
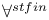 85 85
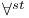 4 14 4 14
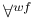 16 16
 58 58
 144 144
 132 132
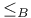 362 380 362 380
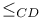 362 380 362 380
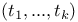 274 274
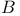 111 111
![$\mathbb{E}[\textit{f}]$](/math_tex/b646597c39694c51e7de1cc7311a100b82.gif) 245 245
 28 28
 in in 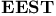 190 190
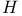 , a model of , a model of 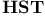 258 258
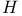 -class 260 -class 260
![$\mathbb{H}[G]$](/math_tex/c6fb6dbcb872b8b5ee5ce48bba487b5582.gif) 261 261
 180 184 180 184
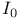 258 258
 230 230
 in IST and BST 111 in IST and BST 111
![$\mathbb{L}[\mathbb{I}_{k}]$](/math_tex/36ecbfc60acdb7c6a89bef20e0ffbd1f82.gif) 248 248
![$\mathbb{L}[\textit{f}]$](/math_tex/f92dd2e5ff6f39a80dbdab05cedc49d082.gif) 245 245
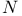 26 26
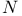 -sequence 307 -sequence 307
![$\mathbb{N}[\textit{w}]$](/math_tex/707285d4ffe39c3416ba3f3254f39a0c82.gif) 223 224 223 224
![$\mathbb{N}_{M}[w]$](/math_tex/80e95007f49ac5d1f3712949d3b7d76a82.gif) 224 224
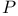 , product forcing 280 , product forcing 280
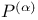 203 203
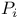 280 280
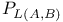 276 276
 54 54
 54 54
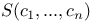 89 221 89 221
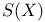 221 221
![$\mathbb{S}[\textit{w}]$](/math_tex/d5fea4344f35e213b40d5851e597be7f82.gif) 89 221 222 89 221 222
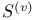 134 134
![$\mathbb{S}_{M}[w]$](/math_tex/ec0cc6adf8d0852a003651b1dfb12aa682.gif) 224 224
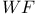 16 16
![$\mathbb{WF}[U]$](/math_tex/45dee07c6ae81ca3542d78d56ffd8bdc82.gif) 44 44
![$\mathbb{WF}[\textit{f}]$](/math_tex/ea9f99d4d35ff0b86feae8d246c0513082.gif) 239 239
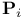 281 281
 170 170
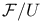 141 141
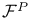 150 150
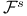 150 150
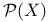 10 21 23 10 21 23
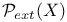 104 104
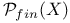 27 27
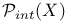 23 32 23 32
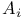 280 280
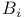 280 280
| ![$\mathfrak{C}[D]$](/math_tex/e9c4fb3095bf4e8e440bc6b3fbf3e4d982.gif) 275 275
 280 280
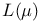 352 352
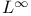 275 275
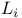 280 280
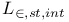 290 290
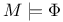 10 48 10 48
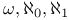 10 25 10 25
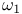 321 321
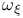 25 25
![$\Phi[G]$](/math_tex/6677c20d202d5622bd9649e28345252582.gif) 266 266
![$\Phi[i]$](/math_tex/52da9626fd6d69fe2dfba39d4674ba7182.gif) 142 142
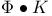 331 331
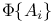 325 325
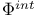 14 14
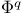 46 46
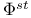 14 14
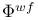 16 16
 111 111
![$\Pi^{0}_{\epsilon}[\mathcal{X}]$](/math_tex/b4825314f105a769c07236f01098612582.gif) 321 321
 33 33
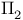 33 33
![$\prod^{0}_{0}[\mathcal{X}]$](/math_tex/f7a80e35977b36928ef5bc2f26e2496282.gif) 321 321
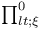 348 348
![$\sum^{0}_{0}[\mathcal{X}]$](/math_tex/3387a34e7cc9f1b33602c3fa7f064c1682.gif) 321 321
![$\sum^{0}_{\varepsilon}[\mathcal{X}]$](/math_tex/545f19157e326e36e287a650d77cf28482.gif) 321 321
 34 34
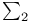 34 34
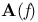 245 245
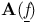 245 245
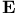 184 184
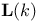 280 280
 184 184
 291 291
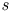 291 291
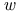 -st x 223 -st x 223
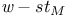 x 224 x 224
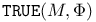 48 48
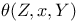 116 118 116 118
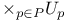 150 150
 197 197
 184 184
 364 364
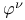 141 141
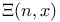 164 164
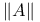 282 282
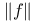 150 150
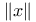 149 149
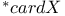 25 25
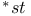 141 141
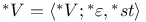 141 141
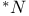 26 26
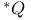 54 54
 54 54
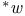 16 16
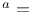 199 199
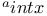 199 199
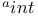 199 199
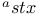 199 199
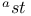 199 199
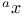 193 193
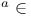 199 199
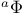 202 202
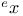 103 103
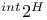 321 321
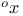 56 56
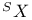 15 15
 85 85
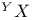 10 10
 184 184
 184 184
 184 184
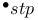 184 184
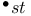 184 184
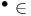 184 184
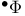 185 185
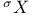 14 85 14 85
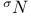 90 90
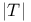 192 192
 197 197
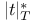 197 197
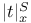 296 296
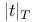 192 192
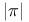 280 280
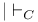 282 282
*-rational 54
*-real 54
= 141
A 324 325
A-code 192
Absolute formula 23
Absolute operation 23
Absolute set 23
Alephs 25
Algebra 321
Asterisks 16
atom 304
Axiom of costructibility 159
Axiom, 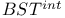 182 182
Axiom, 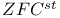 14 84 14 84
Axiom,  -Boundedness 241 -Boundedness 241
Axiom,  -deep BI 105 -deep BI 105
Axiom,  -size BE 138 -size BE 138
Axiom,  -size BI 105 -size BI 105
Axiom, Basic Enlargement 87
Axiom, Basic Idealization 86
Axiom, Bounded Inner Transfer 125
Axiom, Choice 21
Axiom, Choice, 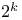 -size Choice 241 -size Choice 241
Axiom, Choice, c-size 319
Axiom, Collection 21
Axiom, comprehension 20
Axiom, Dependent Choice 19
Axiom, Enlargement 86
Axiom, Extensionality 20
Axiom, Global Choice 148 303
Axiom, Idealization 85
Axiom, III-founded Mostowski Collapse 303
Axiom, Infinity 21
Axiom, Inner  -Boundedness 105 -Boundedness 105
Axiom, Inner Boundedness 86
Axiom, Inner Standardization 85
Axiom, Inner Strong  -Boundedness 105 -Boundedness 105
Axiom, Inner Transfer 84
Axiom, Internal Size Collection 298
Axiom, Minimality 159
Axiom, Pair 20
Axiom, Parametrization 182
Axiom, power set 21
Axiom, Regularity 21
Axiom, Regularity over 0 15
Axiom, Replacement 21
Axiom, Saturation 19
Axiom, Saturation,  -deep 241 -deep 241
Axiom, Saturation,  -size 241 -size 241
Axiom, Separation 20
Axiom, SMA 294
Axiom, Special Model Axiom 294
Axiom, Standard Condensation 297
Axiom, Standard Size Choice 19
Axiom, Standard Size Collection 297
Axiom, Standardization 15
Axiom, SuperUniversality 303
Axiom, Transfer 15
Axiom, Transitivity of 0 15
Axiom, union 21
Axiom, Universality 303
Axiom, “![$\mathbb{H}=\mathbb{L}[\mathbb{I}]$](/math_tex/e08e9208474389d5e7686befab553a5882.gif) ” 214 ” 214
A[G] 261
B-smooth 381
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



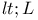
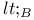

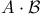
![$a^{put}[G]$](/math_tex/156c75acc81dce75c2e3f28c86cc8f7282.gif)
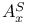
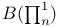
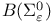
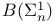
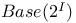
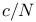
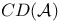

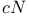

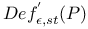
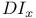
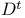
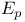


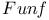
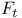
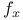

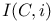
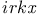
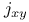
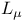
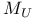
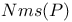
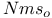
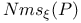
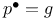
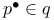
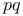

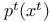
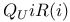

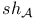 ”X
”X 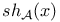
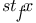
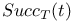

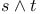
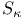
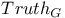 T, modified truth predicate
T, modified truth predicate 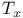
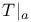
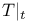
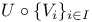

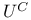
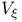
![$V_{\xi}[U]$](/math_tex/0cb11dc2afd77467890f32a4ed9f231682.gif)
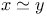
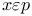
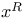
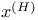


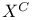
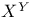
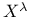
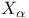

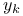
![$[x]^{a}$](/math_tex/f141c076963767906c37b369109c272b82.gif)
![$[\Phi]$](/math_tex/a6e30be8d42b03947fb3a75575c9c63a82.gif)
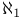
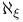

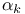
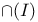
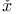
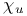
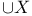
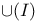
![$\Delta^{0}_{0}[\mathcal{X}]$](/math_tex/f77c9ea56146cb9926eba836bf19723482.gif)
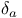

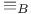
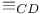
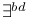
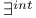
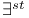
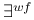
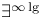
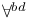
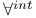
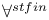
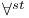
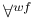



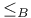
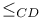
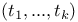
![$\mathbb{E}[\textit{f}]$](/math_tex/b646597c39694c51e7de1cc7311a100b82.gif)

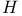 , a model of
, a model of 
![$\mathbb{H}[G]$](/math_tex/c6fb6dbcb872b8b5ee5ce48bba487b5582.gif)

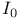

![$\mathbb{L}[\mathbb{I}_{k}]$](/math_tex/36ecbfc60acdb7c6a89bef20e0ffbd1f82.gif)
![$\mathbb{L}[\textit{f}]$](/math_tex/f92dd2e5ff6f39a80dbdab05cedc49d082.gif)
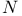
![$\mathbb{N}[\textit{w}]$](/math_tex/707285d4ffe39c3416ba3f3254f39a0c82.gif)
![$\mathbb{N}_{M}[w]$](/math_tex/80e95007f49ac5d1f3712949d3b7d76a82.gif)
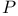 , product forcing
, product forcing 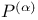
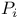
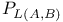


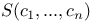
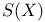
![$\mathbb{S}[\textit{w}]$](/math_tex/d5fea4344f35e213b40d5851e597be7f82.gif)
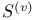
![$\mathbb{S}_{M}[w]$](/math_tex/ec0cc6adf8d0852a003651b1dfb12aa682.gif)
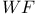
![$\mathbb{WF}[U]$](/math_tex/45dee07c6ae81ca3542d78d56ffd8bdc82.gif)
![$\mathbb{WF}[\textit{f}]$](/math_tex/ea9f99d4d35ff0b86feae8d246c0513082.gif)
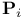

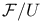
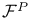
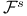
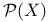
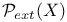
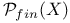
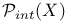
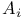
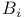
![$\mathfrak{C}[D]$](/math_tex/e9c4fb3095bf4e8e440bc6b3fbf3e4d982.gif)

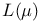
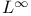
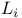
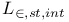
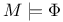
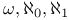
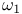
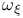
![$\Phi[G]$](/math_tex/6677c20d202d5622bd9649e28345252582.gif)
![$\Phi[i]$](/math_tex/52da9626fd6d69fe2dfba39d4674ba7182.gif)
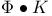
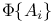
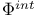
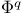
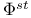
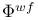

![$\Pi^{0}_{\epsilon}[\mathcal{X}]$](/math_tex/b4825314f105a769c07236f01098612582.gif)

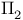
![$\prod^{0}_{0}[\mathcal{X}]$](/math_tex/f7a80e35977b36928ef5bc2f26e2496282.gif)
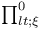
![$\sum^{0}_{0}[\mathcal{X}]$](/math_tex/3387a34e7cc9f1b33602c3fa7f064c1682.gif)
![$\sum^{0}_{\varepsilon}[\mathcal{X}]$](/math_tex/545f19157e326e36e287a650d77cf28482.gif)

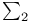
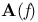
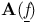
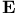
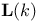
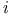
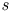
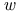 -st x
-st x 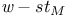 x
x 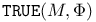
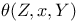
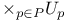



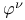
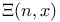
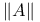
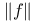
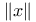
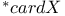
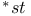
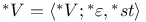
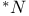
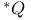

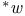
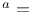
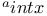
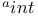
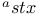
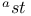
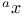
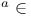
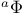
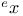
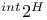
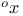
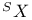

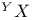

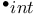
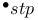
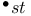
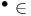
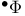
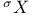
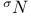
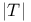

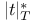
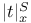
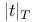
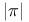
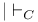
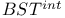
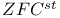
 -Boundedness
-Boundedness 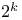 -size Choice
-size Choice ![$\mathbb{H}=\mathbb{L}[\mathbb{I}]$](/math_tex/e08e9208474389d5e7686befab553a5882.gif) ”
”