|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Aldous J.M., Wilson R. — Graphs and Applications: An Introductory Approach |
|
|
 |
| Предметный указатель |
Heuristic algorithm for vertex colouring 288
Hierarchical tree 140
I(d) 125
I(G) 123
icosahedron 46 270 272
Icosian game 71
if 352
If and only if 352
In-degree 92
In-degree sequence 93
Incidence matrix 123 125
incident 27 86
Incompatible edges 257
Indirect proof 349
Induction 350
Infinite face 248
Instant Insanity 51
Interpersonal relationships 53
Interval graph 127
Irreducible Markov chain 132
Isomer 4 175
Isomer enumeration 175
Isomorphic digraphs 87
Isomorphic graphs 29
Isomorphism 29
Join 6 16 26 85
Joocy-chunks 106
k-colourable graph 279
k-colouring 279
k-cube 50 81
k-dimensional cube 50 81
k-edge colourable graph 304
k-edge colouring 304
Kekule, A. 180
Kempe, A. 295
Kirchhoff, G. 139
Knight's tour problem 79 333
Koenig's Theorem 311
Koenig, D. 311
Koenigsberg bridges problem 9 20 64 333
Kruskal's algorithm 184 185
Kruskal, J. 184
Kuratowski's theorem 261
Kuratowski, K. 261
Labelled graph 32
Legendre, A.M. 271
Length of walk 39 95
Line graph 58
Listing problem 22
Listing, J.B. 77
Location of transmitting stations 297
London Underground 2
Longest path problem 337 344
Loop 26 85
Lower bound for 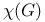 284 284
Lower bound for 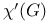 309 309
Lower bound for solution to Travelling Salesman Problem 194 196
Lower bound for t(G) 323
Main diagonal 114
Map colouring problem 293
Markov chain 131
Markov chain, irreducible 132
Matching 318
Mathematical induction 350
Mathematical statement 348
Matrix 113
Matrix, adjacency 113 115
Matrix, incidence 123 125
Matrix, overlap 128
Matrix, transition 131
Maze 8
Menger's theorem for digraphs (arc form) 232
Menger's theorem for digraphs (vertex form) 235
Menger's theorem for graphs (edge form) 229
Menger's theorem for graphs (vertex form) 234
Menger, K. 235
Method of paired comparisons 106
Methods of proof 348—353
Minimally braced framework 159
Minimum bracing 159
Minimum bracing, new from old 159 162
Minimum connector 183
Minimum connector problem 184 337 338
Minimum dominating set 297 338
Minimum spanning tree 183
Model 19
Multiple arcs 85
Multiple edges 26
Mutation 128
Necessary and sufficient condition 352
Necessary condition 352
Negative feedback cycle 102
nested parentheses 151
Network 17
Network, pipeline 18
Network, road 17
Network, social 53 101
Network, telecommunication 17 236
Niche overlap graph 100
Non-deterministic computer 340
Non-deterministic polynomial-time problem 340
Non-planar graph 244
NP 340
NP-complete problem 342 344
NP-problem 340
Null graph 45
O(N) 334
octahedron 46 270 272
Only if 352
Open trail 42
Open walk 42
Optimal connectivity 237
Optimization problem 20 23 337
Ore's Theorem 73
Ore, O. 73
Orientable graph 109
Out-degree 92
Out-degree sequence 93
Outcomes of experiments 147
Over-braced framework 10
Overlap matrix 128
P 340
P-problem 340
Paraffin 3 175
Path 40 95
Path graph 50
Path, semi-Hamiltonian 74
Path, st- 226 231
Petersen graph 47 144 255 262
Petersen, J. 47
Pipeline network 18
Planar graph 244
Planarity testing 256 263
Plane drawing 244
Platonic graph 46
Platonic solid 46 270 273
Platonic solid, dual of 273
Poinsot, L. 77
Polynomial-time algorithm 338 339
Polynomial-time problem 340
Polynomial-time reducibility 342
Positive feedback cycle 102
Potential 204
Prim's algorithm 188 189 337 338
| Principle of Mathematical Induction 350
Principle of strong induction 350
Printed circuits 5 243 321
Proof by contradiction 349
Proof by mathematical induction 350
Proof direct 349
Proof indirect 349
Proof involving if and only if 352
Pruefer sequence 165
Pruefer's construction 165
Pruefer, H. 165
r-Regular Graph 43
Random walk 130
Ranking in tournaments 106
Rectangular framework 10 20 152
Recurrence relation 171
Reductio ad absurdum 349
Refuse collection 296
Regular graph 43
Regular graph, examples 45—47
Regular polyhedron 269
Reliable telecommunication network 236
Rigid framework 10
Rigidity criterion 154
Road network 17
Root 146
Rooted tree 146
Rooted tree, equivalent forms 150
Rotating drum problem 104
Route-finding 2
Row of rectangular framework 12 153
S(G) 325
Same digraphs 87
Same graphs 7 28
Satisfiability problem 342
Scheduling examinations 319
Semi-Eulerian graph 67
Semi-Eulerian trail 67
Semi-Hamiltonian graph 74
Semi-Hamiltonian path 74
separate 227 231
Sequence dating 126
Seriation 126
Shannon's Theorem 308
Shannon, C.E. 303 307
Shortest path algorithm 204 211 338
Shortest path algorithm, tabular method 206
Shortest path problem 23 204 337 338
Signed digraph 101
Signed graph 54
Simple digraph 85
Simple graph 26
Sink 18
Six colour theorem for planar graphs 284
Snow-ploughing 212 213
Social networks 53 101
Sorting tree 150
Source 18
Spanning forest 161
Spanning subgraph 325
Spanning tree 144 158
Spanning tree, construction of 145 335
Spanning tree, minimum 183
st-paths 226 231
st-paths, arc-disjoint 231
st-paths, edge-disjoint 226
st-paths, vertex-disjoint 226 231
STACK 149
State of Markov chain 131
Statement 348
Stereographic projection 271
Storing chemicals 277 292
Street-cleaning 212 213
Strong induction 350
Strongly connected digraph 96 119
Subdigraph 90
Subdivision of graph 260
Subgraph 33
Subgraph, spanning 325
Sufficient condition 352
t(G) 322
t(G), lower bound for 322 323
Tabular method for shortest path algorithm 206
Telecommunication network 17 236
Teleprinter's problem 104
tetrahedron 46 270 272
Thickness 322
Tour graph 296
Tournament 106
Trail 40 95
Trail, closed 42 95
Trail, eulerian 63 97
Trail, open 42
Trail, semi-Eulerian 67
Transition matrix 131
Transition probability 131
Traveller's problem 62
Travelling salesman problem 13 23 191 337 339 344
Travelling salesman problem, lower bound for solution 196
Travelling salesman problem, upper bound for solution 192
TREE 49
Tree, bicentral 179
Tree, binary 147
Tree, branching 147
Tree, central 179
Tree, conceptual 140
Tree, equivalent definitions of 143
Tree, family 140
Tree, grammatical 148
Tree, hierarchical 140
Tree, minimum spanning 183
Tree, properties of 140
Tree, rooted 146
Tree, sorting 150
Tree, spanning 144
triangle 42
Tutte, W.T. 325
Unbalanced situation 54
Underlying graph 92
Unlabelled digraph 89
Unlabelled graph 31
Upper bounds for 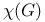 281 282 284 281 282 284
Upper bounds for solution to Travelling Salesman Problem 192
Upper bounds for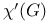 306 307 308 309 306 307 308 309
Utilities problem 4 6 21 28 242 333
Valency 35
Vertex 6 16 26 85
Vertex colouring 277
Vertex connectivity 221 222
Vertex cutset 223
Vertex decomposition 292
Vertex decomposition, colouring problems 292—296
Vertex decomposition, domination problems 296—298
Vertex-disjoint st-paths 226 231
Vizing's theorem 307
Vizing's theorem, extended version 308
Vizing, V.G. 307
Walk 39 95 118
Walk, closed 42 95
Walk, open 42
Weight of edge 13
Weighted graph 13
Whitney, H. 235
Wire-colouring 303 318
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте