|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Polya G. — Problems and Theorems in Analysis: Theory of Functions. Zeros. Polynomials. Determinants. Number Theory. Geometry |
|
|
 |
| Предметный указатель |
Maximum modulus 1
Maximum term 1
Mean domain 56 V 123
Mean value theorem V 95 51 V V VI VI
Meissner, E. 250
Mertens, F. 351
Meusnier, M.Ch. 371
Mills, C.N. 372
Minkowski constant IX 1.2 157 159
Minkowski, H. 56 157 159 371
Mittag-Leffler, G. 204
Modular graph IV 172.1 28
Moebius function 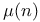 VIII 34 118 VIII VIII 34 118 VIII
Moebius, A.F. 118 313
Moment of a function V 81 48
Montel, P. 237
Montmort, P.R. 306
Moore, E.H. 297
Muentz, Ch.H. 208
Muir, T. 280
Multiplication of Dirichlet series, Dirichlet 119
Multiplication of power series, Cauchy 119
Multiplicative arithmetical function 120
Multiplicative number theory 119
Nagy, J.v.Sz. 232
Neder, L. 361
Net rank 98 99
Netto, E. 313 314
Nevanlinna, F. 171
Nevanlinna, R. 171 195—197 198 211
Norm of a number in an algebraic number field 147
Normed mapping function 16 17
Number of distinct prime factors 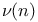 118 118
Number of divisors 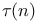 118 118
Number of zeros 1
Obreschkov, N. 211 251
Order of a trigonometric polynomial 72
Order of an entire function IV 51 9 IV
Orthogonal linear transformation 106
Orthogonal matrix 106
Orthogonality condition for generalized Laguerre polynomials VI 99 88
Orthogonality condition for Hermite polynomials VI 100 88
Orthogonality condition for Jacobi (hypergeometric) polynomials VI 98 87
Orthogonality condition for Legendre polynomials 86
Outer radius of a region 16 17
Paley, R.E.A.C. 211
Part 116
Partition of a number AI 20.1 163
Peano curve IV 170 28
Peano, G. 28
Periodic function VI 32 76
Phragmen — Lindeloef method 32
Phragmen, E. 32
Picard exceptional value IV 194 32
Picard, E. 32 35 211
Picard’s Theorem IV 210 35 211
Pick, G. 195 197 342
Planck, M. 218
Plane of support 159
Plank’s law of radiation V 43 218
Plemelj, G. 195
Poincare, H. 203 228 250 367
Point derive d’un point IV 111 231
Polar, first 57
Polya, G., MD 314 317 373
Polya, G., MPR 239 249 257 298 318 337 352 353 372
Polynomial, integral-valued 129
Polynomial, irreducible 132
Polynomial, reducible 132
Polynomial, with integral coefficients 129
Power series with H-integral coefficients 140
Power series with integral coefficients 134 138
Power series with rational coefficients 134
Precise degree of polynomial 54
Prime divisor 130
Primitive power series with integral coefficients VIII 155 137
Primitive roots of unity VIII 36 118
Principal chord IV 149 25
Prouhet, E. 303
Prufer, H. 247 342
Quadratic form 100
Quadratic non-residue V 45 42
Quadratic residue V 45 42
Quasilinearly dependent 100
Rabinowitsch, G. 349
Radicke 303
Radoe, T. 195 196 342
Rados, G. 283
Rational function VIII 149 136 VIII
Rational independence VIII 151 333
Recurrence relation VI 87 86 VII
Recurrent determinant 96
Reducible polynomial 132
Region IV 78 14
Relatively prime numbers 146
Relatively prime numbers, pairwise (coprime) VIII 215 146
Remak, R. 287
Retali 281
| Reversal of sign 39 V
Riemann hypothesis VII 43.1 289 VIII
Riemann zeta function  120 VIII 120 VIII
Riemann, B. 120 155 289 318
Riesz, F. 259
Riesz, M. 30 269 293 294 300
Riordan 290
Roberts, M. 280
Rodrigues, O. 86
Rodrigues’ formula VI 84 86
Rolle, M. 36 37 43 47 51 60 213 229
Rolle’s Theorem 36 V 43 V 51 V V V
Rosenbaum, J. 366
Rotation theorem IV 151 196
Roth, A. 205
Runge, C. 217
Sadier, J. 260
Sarantopoulos, S. 237
Saxer, W. 248
Scherrer, W. 354 355
Schlicht (univalent) function IV 77 14
Schmidt, H. 211
Schoenberg, I.J. 218
Scholl, K. 369
Schreiber, M. 317
Schur, I. 203 238—240 247 251 266 267 286 289 292 294 326 327
Schwarz, H.A. 200 208 228
Serret, J.A. 324
Sidon, S. 359
Siegel, C. 251 324
simple harmonic motion VI 61 80
Sine polynomial 72
Skolem, Th. 341 353
Slit region IV 90 16 IV
Speiser, A. 336 354
Star-shaped closed curve IV 133 22
Star-shaped region IV 161 26 IV
Staudt, K.G.Ch.v. 339
Steinig, J. 218 226
Steinitz, E. 373
Stfickel, P. 325 330
Stieltjes integral VII 66 297
Stieltjes, T.J. 228 297
Stirling numbers of the first and second kind VII 54.2 107
Stirling, J. 9 107 180 181
Stirling’s formula IV 50 9 IV IV
Stoll, A. 284
Study, E. 198
Suess, W. 367
Sum of divisors  118 118
Sum of powers of divisors  118 118
Support function 158 159
Supporting line 7
Sylvester, J.J. 223 224 303 305
Symmetric relation VIII 221 147
Szaesz, O. 211 264 288 361
Szegoe, G. 195 211 237—239 250 252 258 283 298 300 342 360 361 367
Taylor, B. 361
Tchakalov, L. 210 211
Tchebotarev, N. 201 211
Tchebychev condition VIII 154 137
Tchebychev polynomial 71 VI
Tchebychev theorem VIII 249 153 VIII 358
Tchebychev, P. 71 81 137 153 264 358 361
Teixeira, F.G. 331
Titchmarsh (textbook) 10 211
Titchmarsh, E.C. 294
Toeplitz form 110 VII VII VII VII
Toeplitz, O. 110 298
Towber, J. 317
Transitive relation VIII 221 147
Trigonometric polynomial 71—73 77 78
Turaen, P. 354
Unitary transformation IV 207 34
UNITS 146
Univalent (schlicht) mapping IV 77 14
Valiron, G. 167 171 208 247
Vandermonde determinant V 48 43
Vandermonde, A. 43
Vertical pair VII 22 97
Visible arc IV 133 22
Walsh, J.L. 233
Weierstrass 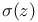 function IV 49 9 function IV 49 9
Weierstrass preparation theorem VIII 152 334
Weierstrass, K. 9 334
Weill, M. 331
Weyl, H. 352
Wiener, N. 211
Wilson, J. 339
Wilson’s Theorem VIII 180 339
Wiman, A. 167 176 207 208
Wronski, H. 50 108 198 226 227 230
Wronskian determinant V 87 50 108
Young, G.Ch. 361
Young, W.H. 256 361
Yule, U. 305
Zero of a polynomial 54 69
Zeta function  120 VIII 120 VIII
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте


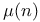
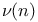
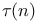



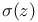 function
function