Авторизация
Поиск по указателям
Goryunov V.I., Lyashko O.V. — Dynamical Systems VI: Singularity Theory I, Vol. 6
Обсудите книгу на научном форуме Нашли опечатку?
Название: Dynamical Systems VI: Singularity Theory I, Vol. 6Авторы: Goryunov V.I., Lyashko O.V. Аннотация: The theory of singularities is an important part of various branches of mathematics: algebraic geometry, differential topology, geometric optics, etc. Here the focus is on the singularities of smooth maps and applications to dynamical systems - in particular, bifurcations. This includes the study of bifurcations of intersections of stable and unstable cycles. Along with the formal algebraic and analytic aspects of the theory, the authors consider global topological problems related to invariants. The authors have in mind a student reader, mathematician, or physicist, who wishes to learn the modern techniques of local mathematical analysis as an instrument for applied studies or a specialist in one of the applied areas who is looking for the necessary mathematical tools.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1993Количество страниц: 245Добавлена в каталог: 08.04.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Map, stable 149 Map, stratified 180 Map, transverse to a submanifold 151 Map, Vieta 123 Map, Whitney 68 Maps, transversality 152 Markushevich, A.I. 87 231 Martinet, J. 156 170 231 Maslov index 192 Maslov, V.P. 192 231 Mather, J. 17 151 154 156 157 160—162 170 171 175 179 180 231 Matov, V.I. 181 182 231 Maurin map 191 Maxwell stratum 208 May, J.P. 140 225 McCrory, C. 217 231 McKay, J. 134 231 Milnor fibration 69 Milnor lattice 84 Milnor, J. 12 19 39 40 51 139 202 221 232 Miniversal deformation 15 Minkowski volume, mixed 162 Mirror 119 Modality 16 18 Modality, intrinsic 45 Module over a system of rings 171 Monodromy operator along a loop 57 Monodromy operator, classical 53 Monomial 35 37 Monomial, diagonal 42 Monomial, lower 42 Monomial, upper 42 Morin, B. 154 157 158 191 232 Morphism of Hodge structures 106 Morphism of mixed Hodge structures 107 Morse (nondegenerate) critical point 11 Morse function 56 Morsification 56 Morsification, purely real 72 Multigerm 162 Multiplicity of a critical point 13 Multiplicity of a germ 161 Multiplicity, algebraic 161 Multiplicity, geometric 161 Multisingularity 204 Mumford, D. 103 229 Muraviev, V.V. 33 34 Napoleon, B. 7 Nekhoroshev, N.N. 71 229 Newton degree of a monomial 45 Newton diagram 35 Newton diagram, suitable 103 Newton filtration 45 Newton order of a series 45 Newton polyhedron 35 162 Newton-homogeneous function 45 Nikulin, V.V. 30 226 Nilsson, N. 97 232 Normal form 22 Number, characteristic 205 Number, Coxeter 122 Number, Hodge 111 Number, Petrovski 118 Ole 118 223 232 Operator, semisimple 109 Operator, unipotent 109 Operator, variation 53 Order of a diffeomorphism 41 Order of a geometric section 108 Order of a series 37 Order of a series, Newton 45 Order of a vector field 41 Order of determinacy of a germ 174 Orlik, P. 39 40 232 Oval 118 Pair of dimensions, nice 160 Pair of dimensions, semi-nice 160 Palamodov, V.P. 161 232 Parabolic singularity 82 Pellikaan, R. 169 170 232 Period map 91 Period map, associated 99 Period map, infinitesimally nondegenerate 100 Period map, principal 102 Period map, stable 100 Perron, P. 71 232 Petrovski 118 232 Petrovskii number 118 Pham singularity 77 Pham, F. 71 77 89 232 Phillips, A. 214 215 232 Picard — Fuchs equation 96 Picard — Lefschetz operator 59 Picard, E. 51 56 232 Pinkham, H. 86 232 Platonova, O.A. 217 Po 168 171 214 233 Poincar 39 Polar curve 78 Polterovich, L.V. 211 224 Pontryagin class 192 Porteous, I.R. 159 160 188—191 233 Poston, T. 221 233 Primitive ideal 169 Principal part of a geometric section 108 Principal part of a series 103 Quadratic form of a singularity 64 Quasihomogeneous function 36 Quasihomogeneous function, nondegenerate 36 Ramanujam, C.P. 70 230 Real function 72 Reflection 119 Regular singularity of a differential equation 96 Residue form 92 Resolution of singularities 26 103 188 Roberts, M. 168 233 Rokhlin, V.A. 138 233 Ronga, F. 168 183 188—190 201 233 Root of a quasihomogeneous algebra 43 Root system 127 Rossi, H. 91 93 228 Saint — Donat, B. 103 229 Saito, K. 40 85 100 134 233 Saito, M. 232 Samo 233 Sauvage, L. 96 Schaeffer, D. 168 169 221 228 Schmid, W. 108 109 228 233 Schwarz, G. 171 233 Sebastiani, M. 76 77 94 233 Section 89 Section, covariantly constant 89 Section, geometric 92 Section, holomorphic 89 Section, nondegenerate 98 Segal, G.B. 141 233 Semi-quasihomogeneous function 37 Semi-quasihomogeneous series 37 Semicontinuity set of the spectrum 114 Semisimple operator 109 Serganova, V.V. 34 71 Series of singularities 23 Series, 104 Series, semi-quasihomogeneous 37 Serre, J. — P. 91 109 234 Set of spectral pairs 111 Sharko, V.V. 207 234 Shcherbak, O.P. 217 Shifrin, T. 217 231 Shil’nikov, L.P. 222 Shoshita 38 234 Shustin, E.I. 8 218 234 Shvarts, A.S. 142 234 Siersma, D. 132 169 234 Simart, G. 56 232 Simple function 18 Simple loop 59 69 Simple singularity 20 Singer, I.M. 119 223 Singularities, almost equivalence 147 Singularity 11 Singularity, bimodal 18 Singularity, elliptic 82 Singularity, hyperbolic 83 Singularity, of class 154 Singularity, parabolic 82 Singularity, Pham 77 Singularity, regular, of a differential equation 96 Singularity, simple 20 Singularity, tangential 216 Singularity, unimodal 18 Slodowy, P. 26 234 Smale, S. 142 213 214 234 Solomon, L. 126 234 Spectral pair 111 Spectrum of a singularity 111 Springer, T.A. 123 234 Stable cohomology class of complements of discriminants 145 Stagnaro, E. 117 234 Stasheff, J.D. 139 202 232 Steenbrink, J.H.M. 95 105 110 112 114 116 234 Stewart, I.N. 221 233 Stiefel — Whitney class 139 Stiefel — Whitney class, total 188 Stiefel — Whitney class, universal 139 Stratified submanifold 152 Stratum, 18 Subgroup, geometric 172 Subgroup, nice geometric 173 Subgroup, strongly closed 177 Support of a power series 35 Support of a quasihomogeneous function 43 Swallowtail 19 Swallowtail, generalized 123 Swallowtail, unfurled 211 System of ideals 171 System of paths, admissible 79 System of paths, distinguished 60 System of paths, weakly distinguished 60 System of rings 171 System of rings, adequately ordered 171 System of sets, stable 187 Sz 202 234 Tangential singularity 216 Teissier, B. 20 78 183 234 Thom polynomial 186 187 Thom, R. 76 77 151 180 181 187 193 196 212 233—235 Timourian, I.G. 71 235 Togliatti, E. 117 235 Topological complexity of an algorithm 142 Tougeron, J. — C. 14 235 Trivialization 93 Trotman, DJ.A. 152 180 235 Truncated versal deformation 20 Tyrina, G.N. 17 82 235 Unimodal function 18 Unimodal singularity 18 Unipotent operator 109 Va 125 140 235 Vanishing cohomology bundle 90 Vanishing cycle 55 58 Vanishing homology bundle 90 Vanishing inflection 217 Varchenko, A.N. 18 20 33 38 45 71 83 87 93—95 98 101 104 105 108—112 114—117 119 130 132 151 161 163 181 211 221 223 235 236 Variation operator 53 Varley, R. 217 231 Vasil’ev, V.A. 9 23 34 141—143 145—147 161 165 169 170 174 183 191 194 197—200 204—206 216 223 236 Vector field (formal) 41 Versal deformation 15 17 167 Vieta map 123 Vinberg, E.B. 34 Viro, O.Ya 118 219 236 237 w.h.e.-principle 213 Wagreich, P. 39 232 Wajnryb, B. 87 237 Wall, C.T.C. 136 160 161 167 174 175 178 179 237 Walls of a chamber 120 Wassermann, G. 168 237 Weight filtration 107 109 Weinstein, A. 12 237 Wells, R.O. 106 237 Weyl group 127 Whitney conditions a and b 179 Whitney map 68 Whitney stratification 180 Whitney umbrella 150 Whitney umbrella, unfolded 203 Whitney, H. 14 71 149 179 180 212 237 Wilson, L.C. 174 178 237 Wirthm 179 183 227 237 Zakalyukin, V.M. 33 126 168 237 Zeta function of monodromy 102
Реклама
 |
|
О проекте
|
|
О проекте



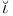
 naru, V.
naru, V.  -nondegenerate
-nondegenerate 
 = const
= const  cz, A.
cz, A.