|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Rockingham G.R. Ч Deducibility and Decidability |
|
|
 |
| ѕредметный указатель |
 69 69
 64Ч66 68 69 107 64Ч66 68 69 107
 68 68
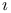 68 84 68 84
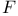 140 140
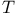 140 140
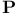 15 72 89Ч98 105Ч108 114 128Ч131 15 72 89Ч98 105Ч108 114 128Ч131
 130 130
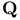 75 22 72 108 114 117Ч118 129 75 22 72 108 114 117Ч118 129
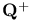 , , 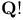 21 21
 , , 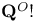 , , 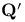 22 22
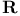 75 72 98Ч99 110 116Ч117 121 129 75 72 98Ч99 110 116Ч117 121 129
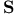 1 2Ч4 72 98 1 2Ч4 72 98
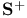 4Ч5 4Ч5
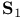 see УKleeneФ see УKleeneФ
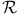 93 93
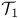 see УKleeneФ see УKleeneФ
 -completeness see УProperty -completeness see УProperty
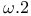 96 fn. 96 fn.
 , ,  , , 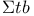 68Ч69 68Ч69
 2 61Ч62 2 61Ч62
 -provable 26 46 -provable 26 46
 -provable, -provable,  69 86Ч87 106Ч108 114 121 69 86Ч87 106Ч108 114 121
 -provable, -provable,  , ,  126Ч127 128 126Ч127 128
 -provable, -provable, 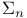 -, -, 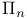 -provable 125 126 -provable 125 126
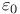 96 fn. 97 104 96 fn. 97 104
 , , 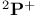 114 114
A 8 137 142
Ackermann, W. 87 112 119
Adequacy Theorem 131 148
ap, 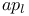 68 68
Application (formal), [ ] 139
Application (formal), [ ], ap 68
Application (formal), [ ], Application Principle 142 149
Application (formal), [ ], pap 84
Application (formal), [ ], partial application (formal), [ ] 85
Application (informal) 73Ч74 79Ч80 134Ч135
Arbib, M.A. 122
Argument 135
Arithmetical concepts 8 89 97 111
Arithmetization 59Ч72 esp. 65Ч66 106 107 108
Arkadencafe (Vienna) 101
Ars Combinatoria see УLeibnizФ
Assign/ment, | | 140 f. 148
Assign/ment, | |, being standardly assigned T 90 109 111Ч115 119 142
Assign/ment, | |, Putnam assign/ment, | | 131
Assign/ment, | |, standard assign/ment, | | 142 (see also УModelФ)
Axiomatization 8 89
B 11
BD 55
Begriffsschrift 67 100
Benacerraf, P. 7
Bernays, P. 131
Berry, G.G. 4
Beth numbers 50 53
Beth, E.W. 6
Binary (notation, representation) 95
Branch 32Ч34 143
Brouwer Ч Koenig Infinity Lemma 33Ч36
Brouwer, L.E.J. 33 35 101
Buridan, J. 78 84
Cantor's argument 10 37 73 81 110
Cantor, G. 10 60 96
Cargile, J. 76
Carnap on definite descriptions 141Ч142
Carnap on syntax 65Ч66
Carnap's Fixed-point Lemma 83Ч84 89Ч98 130
Carnap's fixed-point, C 82Ч85 89Ч98 109 115 117 126 130
Carnap, carn 85
Carnap, R. 101Ч102
casus 86
Category-mistake 75
Chain 32Ч33
Chandra, A.K. 39
Charles II 113
Choice see УFunctionФ
Chomsky, A.N. 67
Church's Theorem 117Ч119
Church's thesis 40Ч43 47Ч49 57 72 84 115 116
Church, A. 45 60 66Ч67 79 115
Cichon, E.A. 95
Classification 78
Clos/ed, closure  , ,  69 69
Clos/ed, closure of  -tableaux 24 -tableaux 24
Clos/ed, closure of regular tableaux 145
Clos/ed, closure, Rgcl, Clrgtb 71
Closure condition 147
Clrgtb 71
cnjn 64
Co-denoting 135
Co-extensive 8 43f. 55 57 114 135
Cock Robin 35 43
Code number see УEncodingФ
Cohen, L.J. 86
Compatibility, formal 117 118 130
Complement 44 46 135
Complete/ness 4Ч5 14 18Ч19 19Ч22 67 89 148Ч149 110
composition 85
Composition, comp 85
Concatenation 58 136
Concatenation, 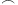 58 58
Confirm/ation, confirm/ation ability 40 43Ч44 УProcedureФ)
Congruen/t, congruence 83 138
conjugate 143
Conjugate,  144 144
Connected/ness 1 5 6 93
Connectives 136
Consisten/t, consistency 90 91 93 110 147 148
Constructive choice function 121
Constructive techniques 20Ч22 90Ч91
Constructive truth 35Ч36 110
Constructivists 90 93 121
Continuum, uncountability of 10
Convention T 114
Corners,  1 (see also УQuotationФ) 1 (see also УQuotationФ)
Correctness Theorem 131 148
Cretan/s see УParadox LiarФ
Cross-reference 83Ч84
Curry, H.B. 79
Cut-free 145 148
Cut-Rule 144 148
Dash/ing 2 61Ч62
Dash/ing, dash 62 68
Davidson, D. 67 112 113
Davis, M. 40
Dbl 89
Ddn 89
de Fermat, P. 35 43
Deci/sion, lability 67 72 115Ч118 120 УProcedureФ)
Dedekind, R. 4 15 50Ч51
Deduc/tion, cf. 115Ч118
Deduc/tion, deducibility, formal, 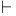 3 16 19 101 145 3 16 19 101 145
Deduc/tion, deducibility, formal, 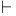 , Deducible, Dbl 89Ч98 105Ч108 126 128Ч131 , Deducible, Dbl 89Ч98 105Ч108 126 128Ч131
Deduc/tion, deducibility, formal, 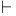 , Fmddn, Fmdbl 70 72 , Fmddn, Fmdbl 70 72
Definition 8 105 114Ч115
Definition, recursive 49 f. 86Ч87 111
Degree see УSentence-formФ
denote 78 135
Descend/ant, descendance-chain see УSentence-formФ
Description operator 14 136 142 149
Descriptions, definite 141Ч142
Descriptor 135
Descriptor-form 139
Descriptor-form,  -descriptor-form 23 56 -descriptor-form 23 56
Descriptor-form,  -descriptor-form 23 -descriptor-form 23
Descriptor-form, Dscfm 67
Descriptor-letter see УLetter/sФ
diag 82
diagg 85
Diagonal, diagonal argument, diagonal procedure 73 102
| Diagonalization 73Ч88
Diagonalization of a predicate 73 90 110
Diagonalization of a predicate-form 82 85 90
Diagonalization, diag 82
Diagonalization, diagg 85
DICTIONARY 20 139
Dictionary, standard dictionary 139Ч140
Dirichlet, P.G.L. 20 108
Disconfirm/ation, disconfirmability 44 (see also УPredicateФ УProcedureФ)
Domain 45Ч48 135
Dreben, B. 120
Dscfm 67
dsjn 64
Dummett, M.A.E. 4 35 103 134
e 8 137 142
Edwards, H. 35 65
Effective/ness 80 (see also УProcedureФ УRelationФ УFunctionФ УOperationФ УLetter/sФ)
Ehrenfeucht, A. 122
Elementary 56Ч57 70
Eliminability 130
Enc 54
Encod/e, enc 54
Encod/e, encoding 52Ч53
Enderton, H.B. 9
Entscheidungsproblem 117 119Ч120
Epimenides see УParadox LiarФ
Equivalence, analytical equivalence 76
Equivalence, elementary equivalence 6
Equivalence, local, global equivalence 107 114
Etchemendy, J. 113
Eubulides see УParadox LiarФ
Euclid 20Ч21
Expressions, formal 10 137Ч139
Extension of predicate 8Ч9 44Ч47 115 135
Extension of sequence 33
Extension of set 15 130Ч131 147
Extension rules for tableaux 26 125 143
Extensionality 4 9 135
Extensionality, cf. 105
Feferman, S. 46 84 92 93 94 129
Finit/ary, fistic see УHilbert's ProgrammeФ
fit 140
fixed-point see УCarnapФ УFunctionФ УJeroslowФ УMontagueФ
Fmdbl 72 98Ч100 108
Fmddn 70
FN 68
FORM see УSubject- sentence- descriptor-
Form, simple 64 87
Form, top-form 143
Form, tpfm 69
Form, universal-form 21 147
Formal numerals 2
Formal numerals, Fnsq, fn 61Ч64 68
Formal numerals, theoretically dispensable 14
Formal system 100Ч104
free 139
Frege, F.L.G. 4 14 21 50 67 78 100Ч101 103 141 142
Friedman, H. 95 112
Fulfilment 27Ч28 31
Function 45Ч48 136
Function, choice function 120 122 128
Function, fixed-point of a function 82 fn.
Function, propositional function 78 134
G 89Ч92 94 112 126
Geach, P.T. 78 79
Gentzen, G. 97
Geometry 20Ч21
Goedel on mathematical intuition 102Ч103
Goedel's First Theorem 79 99 100Ч103 117
Goedel's second theorem 99 103Ч104 129
Goedel's witness G to 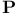 's incompleteness 89Ч92 94 's incompleteness 89Ч92 94
Goedel, K. 9 20 24 42 54 60 67 76 79 83 89 90 91 93 98Ч99 101Ч105 109 110 111 112 117 119 121Ч123
Goedel-number 60
Goedel-number, ** 61 88
Goedel-number, fn 68
Goldfarb, W. 120
Goodstein, R.L., Goodstein's Theorem 95Ч97
Grelling, K. 110
Grounded (form) see УSentence-formФ УInductionФ УHierarchyФ
Grzegorczyk, A. 56
Hallett, M. 10
halt/ing 30 38
Hardy, G.H. 120 fn.
Harrington, L. 95
Haugeland, J. 37
Henkin, L. 92
Heterologicality 110
Hierarchy, arithmetical 124Ч128
Hilbert's Programme 91 103Ч104
Hilbert, D. 60 fn. 87 91 100 103Ч104 111 112 119 131 142
Hook, hk 64
Hook, hkup 71
Hook-up 145
IFF 10 fh.
Imdsc 106
Incompleteness of 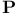 20 89Ч98 105 УGoedelФ) 20 89Ч98 105 УGoedelФ)
Incompleteness of 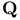 19Ч22 19Ч22
Incompleteness of 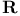 98 98
Incompleteness of 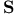 5 98 5 98
Inconsistency see УConsistencyФ
Independence classic independence proofs re-vamped 98
Independence from 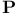 89Ч98 89Ч98
Independence from 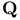 20Ч22 20Ч22
Independence from 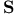 5 5
INDEX see УSentence-formФ
Induction on grounded forms 13
Induction on numbers 3Ч4 15 96Ч97 103 126
Induction on ordinals 96Ч97
Infinit/ary, infinitistic see УHilbert's ProgrammeФ
Intuition, mathematical 102Ч103
Intuitionists see УConstructivistsФ
Irreflexiv/e, Irreflexivity 1 5 6
Isaacson, D. 97Ч98
Isomorphism 6
Jeffrey, R.G. 143
Jeroslow's Fixed-point Lemma 88
Jeroslow's fixed-point, J 88
Jeroslow, jer 88
Jeroslow, R.G. 88
Jones, J.P. 22
Kalmar, L. 56Ч57
Kaplan, D. 79
Kirby, L. 95 96
Kleene, 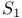 , , 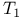 70 (see also УRecursion TheoremФ) 70 (see also УRecursion TheoremФ)
Kleene, S.C. 19 42 69 87 115 116 121 124 131 139
Klein, F. 20
Kneale, W. 77
Kneebone, G. T. 101
Kochen, S. 98
Koenig, J. 33 35 82
Kreisel, G. 60 fn. 106 130
Kripke, S. 98
Kronecker, L. 65 fn.
L 1 137 142
Laius 76
Langford, C.H. 5 9
le Veque, W.J. 20
Leibniz, G.W. v. 118Ч119
Length 136
Length in Mostowski's sense 93 122
Letter/s 66Ч67 136Ч137
Levy, A. 106 fn. 130
Lewis, D. 37
Lewis, H.R. 39 120
Limitations by statute 41 f.
Lingua Philosophica see УLeibnizФ
Lob's Theorem 99
Lob, M.H. 92 94
Lobatschewsky, N.I. 20Ч21
Logic, second-order 87 112 114
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте






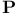

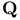
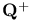 ,
, 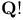
 ,
, 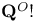 ,
, 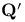
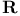
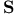
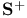
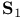
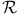
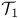
 -completeness
-completeness 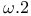
 ,
,  ,
, 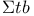


 ,
, 
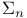 -,
-, 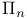 -provable
-provable 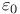
 ,
, 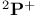
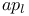
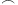


 -descriptor-form
-descriptor-form  ,
,