Авторизация
Поиск по указателям
Hijab O. — Introduction to Calculus and Classical Analysis (Undergraduate Texts in Mathematics)
Обсудите книгу на научном форуме Нашли опечатку?
Название: Introduction to Calculus and Classical Analysis (Undergraduate Texts in Mathematics)Автор: Hijab O. Аннотация: This text is intended for an honors calculus course or for an introduction to analysis. Involving rigorous analysis, computational dexterity, and a breadth of applications, it is ideal for undergraduate majors. The book contains many remarkable features: * complete avoidance of /epsilon-/delta arguments by instead using sequences * definition of the integral as the area under the graph, while area is defined for EVERY subset of the plane * complete avoidance of complex numbers * heavy emphasis on computational problems * applications from many parts of analysis, e.g. convex conjugates, Cantor set, continued fractions, Bessel functions, the zeta functions, and many more * 344 problems with solutions in the back of the book
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: 1st editionГод издания: 1997Количество страниц: 313Добавлена в каталог: 05.04.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
230 207 152 163 7 9 3 9 95 168 181 212 220 213 186 218 206 211 212 180 a | b 10 Absolute value 13 AGM 182 AGM curve 214 Algebraic order 58 angle 100 ArcCos 97 Archimedes’ constant 95 arcsin 97 arctan 99 Area 115 Area, additivity 123 Area, affine invariance 126 Area, dilation invariance 117 Area, monotonicity 118 Area, naive 116 Area, of a parallelogram 122 Area, of a rectangle 119 Area, of a triangle 122 Area, reflection invariance 118 Area, rotation invariance 122 Area, subadditivity 118 Area, translation invariance 116 Arithmetic progressions 223 Asymptotic equality 186 197 218 Asymptotic expansion 230 231 B(x, y) 193 Bailey — Borwein — Plouffe series, bell-shaped curve 189 Bernoulli function 206 Bernoulli numbers 206 Bernoulli series 206 Bessel function 171 181 196 beta function 193 Binomial coefficient 201 Binomial theorem 81 Binomial theorem, Newton’s generalization 91 Bound lower 4 Bound upper 4 Cantor set 111 Cantor set, area of the 126 Cauchy order 35 Cauchy — Schwarz inequality for integrals 152 Cauchy — Schwarz inequality in the plane 101 Chain rule 64 Codomain 2 Compact 39 41 Complement 2 Completeness property 4 Continued fractions 12 25 38 169 174 Continuity 45 Continuity, from the left 50 Continuity, from the right 50 Continuity, in two variables 178 Continuity, modulus of 48 Continuity, under the integral sign 178 Continuity, under the summation sign 180 Continuity, uniform 51 Continuity, uniform modulus of 51 Convex conjugate 81 Cosecant 99 cosh 86 Cosine 94 Cotangent 99 coth 205 Cover 115 Critical point 65 Critical value 65 de Morgan’s law 2 Decimal expansions 27 decimal point 28 Delta function 143 Derivative 61 Derivative, partial 189 Differentiation 61 Differentiation, under the integral sign 189 Differentiation, under the summation sign 195 DIGITS 27 Dilation 6 99 117 Dilation, centered 117 Discontinuity, jump 47 Discontinuity, mild 48 Discontinuity, removable 47 Discontinuity, wild 48 Distance 100 Domain 2 Dominated convergence theorem for integrals 170 Dominated convergence theorem for series 179 Domination 170 Duplication formula 201 Entire 89 entropy 201 Euclidean motion 99 Euler product 222 Euler — Maclaurin, derivative 227 Euler — maclaurin, formula 229 Euler’s constant 152 Even 9 67 Even, part 67 Expansion, base of 28 Expansion, binary 28 Expansion, decimal 27 Expansion, hexadecimal 28 Expansion, ternary 28 Factorial of a natural 28 Factorial of a real 164 Fatou’s Lemma 167 Fourier transform 181 196 Fractional part 10 Functional equation, AGM 186 Functional equation, theta 212 Functional equation, zeta 221 Functions 2 Functions, algebraic 55 Functions, bounded 127 Functions, concave 75 Functions, continuous 45 Functions, convex 75 Functions, decreasing 44 Functions, differentiable 61 Functions, elementary 229 Functions, exponential 57 Functions, increasing 44 Functions, logarithmic 57 Functions, monotone 44 Functions, negative part 128 Functions, nonnegative 127 Functions, positive part 128 Functions, power 55 56 Functions, rational 47 Functions, signed 128 Functions, smooth 74 Functions, strictly concave 75 Functions, strictly convex 75 Functions, strictly decreasing 44 Functions, strictly increasing 44 Functions, strictly monotone 44 Functions, theta 212 Functions, transcendental 56 Fundamental theorem 145 Gamma function 163 Gaussian, function 189 Gaussian, integral 188 Golden mean 38 Greatest integer 10 Heat equation 217 Homogeneity 182 Inductive 7 Inductive, hypothesis 8 Inductive, step 8 inf 4 Infimum 4 Infinite product 203 Infinite product for 210 Infinite product for sin 209 Infinite product for sinh 203 Integrability of nonnegative functions 128 Integrability of signed functions 129 Integral test 140 Integrals, additivity 134 Integrals, continuity 139 Integrals, continuity at the endpoints 137 Integrals, differentiability 144 Integrals, dilation invariance 132 Integrals, integration by parts 148 Integrals, linearity 147 Integrals, monotonicity 131 Integrals, of nonnegative functions 128 Integrals, of signed functions 129 Integrals, substitution 148 Integrals, translation invariance 132 Interior 113 Intermediate value property for continuous functions 50 Intermediate value property for derivatives 74 Intersection 2 interval 12 Interval, compact 13 Interval, open 13 Interval, punctured 42 Inverse function theorem for continuous functions 54 Inverse function theorem for differentiable functions 69 Irrationals 14 Laplace transform 172 195 Laplace transform of 211 Laplace’s theorem 198 Limits from the left 43 Limits from the right 43 Limits lower 19 limits of functions 42 Limits of monotone sequences 18 Limits of sequences 19 Limits upper 19 Log-convex 167 L’Hopital’srule 73 Machin’s formula 108 Maclaurin series 85 Mappings 2 Mappings, bijective 2 Mappings, composition of 2 Mappings, injective 2 Mappings, invertible 3 Mappings, surjective 2 Maximum 5 Maximum principle 81 Maximum, global 65 Maximum, local 65 Mean value theorem 66 Mean value theorem, generalized 72 Mean, arithmetic 182 Mean, arithmetic-geometric 182 Mean, geometric 182 Method of exhaustion 110 153 Minimum 5 Minimum, global 65 Minimum, local 65 Monomial 46 Monotone convergence theorem for integrals 164 Monotone convergence theorem for series 166 Multiplicative 224 n! 28 nth root 14 Numbers, algebraic 58 Numbers, integers 9 Numbers, natural 7 Numbers, rational 9 Numbers, real 3 Numbers, transcendental 58 O(g(x)) 230 Odd 9 67 Odd part 67 Parity 8 Partial sum 25 Partition 44 Partition, mesh of a 52 Paving 115 PI 95 Piecewise, constant 52 136 Piecewise, continuous 147 Piecewise, differentiable 153 Polar coordinates 98 Polynomial 46 Polynomial growth 199 Polynomial, coefficients of a 46 Polynomial, degree of a 46 Power series, differentiability of 89 PRIMES 10 Primitives 102 Primitives, integration by parts 104 Primitives, linearity 104 Primitives, substitution 105 Radius of convergence 88 RANGE 2 Ratio Test 88 Rectangle, compact 40 114 Rectangle, open 40 114 Reflection 6 Relation 2 Remainder 83 Remainder, Cauchy form 84 Remainder, integral form 150 Remainder, Lagrange form 84 Riemann integrable 142 Riemann sum 137 141 Root test 88 Rotation 99 Sawtooth formula 219 Secant 99 SEQUENCE 16 Sequences, bounded 19 Sequences, Cauchy 31 Sequences, convergent 23 Sequences, decreasing 17 Sequences, error 31 Sequences, increasing 17 Sequences, lower 18 Sequences, monotone 18 Sequences, of sets, increasing 154 Sequences, sub- 23 Sequences, upper 18 Series 25 Series, absolutely convergent 31 Series, alternating 30 Series, alternating version 37 Series, cauchy product 37 Series, comparison test 27
Реклама
 |
|
О проекте
|
|
О проекте



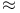



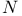




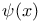


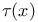

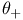 ,
, 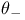 ,
,