|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Franklin J., Daoud A. — Introduction to Proofs in Mathematics |
|
|
 |
| Предметный указатель |
"All" quantifier 39
"All" statements 3 12ff 39
"All" statements, "All As are Bs"form 13
"All" statements, disproof of 48
"All" statements, equivment ways of expressing 17
"All" statements, proof of 13ff
"if and only if" statement 25
"if and only if" statement, "if ... then. .. and conversely" form 30
"if and only if" statement, "necessary and sufficient" form 25
"if and only if" statement, equivalent ways of expressing 25
"if and only if" statement, proof of 26—29
"If" statement 13 17—18
"If" statement, equivalent ways of expressing 17
"If" statement, proof of 13ff
"iff" 25
"many-to-one" function 126
"not-all" statement 48ff 70
"not-all" statement, proof of 48
"only if" statements 17
"some" statements 32
Addition of vectors 86—87
Algorithms 108 131
Aristotle 143—144 146
Arithmetic progression 4—5 83
assertion 7 28
assignment statement 150
Associative law 9 87 98
Axioms 3 87 91 143—145
Axis of symmetry 23 37 46
Bijection, bijective 128—129
Bounded set 73
Calculator 2 4 9 108
Calculus 19—20 24 31 35 38 44 56 71 74 85 100 104
Cantor 120
Cauchy 43 146
Certainty and proof, I 140 143
Chinese 149
Circular argument 156
Closure under addition 92—93
Closure under scalar multiplication 92—93
Codomain 124 129
Combinatorim explosion 118
Commutative law 3 87
Complement of a set 62 117
Compound interest 131—132
Computers 2—3 108 118 147 150—153
Conjectures 9 82 140—142
Constructive existence proof 32 34
Continuity 104—108
Continuous function 34 42 104
Contradiction, proof of 50ff 126
Contradictory of a statement 48
Contrapositive 49 127
Convergence 100ff
Convergent Series 108—109
CONVERSE 17 25
Convex set 73
Correspondence, one-to-one 116—117 128
Counterexample 48ff 95 126 128
Counting 26 116ff
De Morgan laws 73
Deductive logic 140
Dependent, linearly 35 38 44 54—55
Direct proof 49 57
Disproof by counterexample 48 95
Disproof of "All" statement 48
Distributive law 87
Divergent series 108—110
Empty set 67
Equality, functions, of 124
Equality, logic of 91
Equality, sets of 61 63
Equivment statements 20 25 49—50 53 63
Euclid 40 143—144 146
Euclidean geometry 143ff
Euler 26—27 141
Even numbers 20 26 39 50 64
Existential generalisation 32
Existential quantifier 39
Existential quantifier, symbol for 42
Exponential decay 133
Factorial 5
Fallacious argument 7—8
Falling bodies 134—136
Feedback 134
Fermat's Infinite Descent 80
Fermat's last theorem 142
Fermat's Small Theorem 85
Fibonacci sequence 78
Formal logic 146
Four-colour Theorem 147
Frege 146
Function 123ff
Function, "many-to-one" 126
Function, bijective 128—129
Function, codomain of a 124 129
Function, continuous 34 42 104
Function, image of a 125
Function, injective 126—127
Function, limit of a 100—103 114
Function, one-to-one 126—127
Function, onto 125—126
Function, range of a 125
Function, surjective 125—126
Function, vector, as a 99
Fundamental theorem of algebra 42
GaIileo 119 124
Gauss 42
Generalisation, existential 32
Generalisation, universal 12 21
Geometrical progression 37 84
Geometry, proofs in 1 143—144
Global and local structure 132—133
Goedel 145—146
Golden ratio 10
Harmonic series 108
Heaviside 149
hilbert 145
Ideal 65
Image, element, of an 123
Image, function, of a 125
Implication 17
Independent, linearly 55
Induction 82 140—142
Induction, mathematical 76ff
Infinite series 37—38 108
infinity 101—102 119—120
Infinity, primes, of 40
Injective function 126—127
Insight 143 147
Intersection of sets 62
Invariant, loop 152
Irrational numbers 46 48 51—52
Irrationality of  , e and , e and  51—52 51—52
Leibniz 62
LIMIT 100ff
Limit, function at a point, of a 114
Limit, function at infinity, of a 100—103
Limit, sequence, of a 103—104
Linear algebra 18 24 31 34 38 43 54 68 86ff
Linear combinations 18—19 24 34 43 54 68
Linear equations 18 24
| Linearly dependent 35 38 44 54
Linearly independent 55
Local and global structure 132—133
Logic 1 12 17 43—45 131 143
Logic, deductive 140
Logic, non-deductive 140—141 144
Logic, symbolic 146—147
Logically equivalent 20 25 49—50 53 63
Mathematics, I 7 15 145
Mathenurtical induction 76
Matrices as vectors 87
Modelling, mathematical 131—136
Multiple 32
Multiple quantifiers 39—45 100ff
Multiple quantifiers and "not" 53
Necessary and sufficient condition 25
Necessary condition 17
Negation 48
Non-constructive existence proof 33 41
Non-deductive logic 140—141 144
Non-Euclidean geometry 144—145
Numbers, even 20 26 39 50 64
Numbers, irrational 46 48 51—52
Numbers, odd 15ff 50
Numbers, perfect 36
Numbers, prime 30 37 40 80
Numbers, rational 25 31 46 51
Numbers, whole 3 12 26 32 39—41 76
Ob oustruths 1 143—147
Odd numbers 15ff 50
One-to-one correspondence 116—117
One-to-one function 126—127
Onto function 125—126
Oresme 110
Pairing 116ff 128
Particular statements 12
Peano axioms 145
Perfect number 36
PI 11
Pigeonhole Principle 85 159
Platonic solids 25—26
Polyhedra 25—26
Polynomials as vectors 86—89
Population growth 136—137
Predicate 12
Prime number 30 37 40 80
Progression, arithmetic 4—5
Progression, geometric 37 84
proof 1ff
Proof, "all" statement, of 13ff
Proof, "if and only if" statement 26—29
Proof, "if" statement, of 13ff
Proof, "not-all" statement 48ff
Proof, "some" statement, of 32
Proof, computer generated 144
Proof, construction of a 1—2
Proof, constructive existence 32 34
Proof, contradiction, by 500
Proof, counterexample, by 48ff 95
Proof, counting, by 26 116ff
Proof, direct 48 57
Proof, enumeration, by 116
Proof, fallacious 7—8 84
Proof, from axioms 3 91 143
Proof, mathematical induction, by 76ff
Proof, non-constructive existence 33 41
Proof, reductio ad absurdum, by 500 120
Proof, search for a 8
Proof, set equality, of 63—67
Proof, set inclusion, of 63—64
Proof, uniqueness 89—90
Proposition 50 78 144
Pythagoras'theorem 1 23 144
Quantifiers 39ff
Quantifiers, existential 39
Quantifiers, interchange of 42—43
Quantifiers, multiple 39—45
Quantifiers, universal 39
Range of a function 125
Rational numbers 25 31 46 51
Reductio ad absurdum proof 500 120
Regular polyhedron 25
Relation 12
Reversible steps 7 29
Rolle's theorem 60
Round-off errors 3
Russell, D. 145—146
scalar 24 35 43 44 87ff
Scalar multiple 24 38 44
Scalar multiplication 74 86ff
Search for a proof 8
Sequence, limit of a 103—104 112
Series 108
Series, convergent and divergent 108—110
Series, for 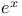 38 38
Series, harmonic 108—110
Sets 17 61ff
Sets, bounded 73
Sets, complement 62
Sets, convex 73—74
Sets, element of 61
Sets, intersection and union of 62
span 68—70
Stability 134
Statement, "all" 3 12ff 39
Statement, "if and only if" 25ff
Statement, "if" 17ff
Statement, "iff" 25
Statement, "not-all" 48 70
Statement, "only if" 17
Statement, "some" 32
Statement, assignment 150
Statement, existential 80
Statement, particular 12
Subject 12
subsets 62—63
Subsets, number of 80—81 116—117
subspace 74 92—95
Sufficient condition 17
Sum of a series 108
Surjective function 125—126
Symbolic logic 146—147
Symmetry, axis, about an 23 37 46
Symmetry, point, about a 23
Truths, mathematics, in 1
Truths, obvious 1 3 5—7 143—147
Union of sets 62
Uniqueness proof 89—90
Universal generalisation 12 21
Universal quantifier 39
Universal quantifier, symbol for 42
Vector space 86ff
Vectors 18—19 34—35 43ff 55 68ff 86ff
Vectors, addition of 87
Vectors, functions as 99
Vectors, matrices as 87
Vectors, scalar multiplication of 87
Venn diagrams 48 62
Weierstrass 146
Whitehead 146
Whole numbers 3 12 26 32 39—41 76
Zero vector 44 87—90
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 , e and
, e and