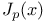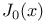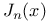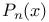|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Jackson D. Ч Fourier Series and Orthogonal Polynomials |
|
|
 |
| ѕредметный указатель |
Asymptotic formula for 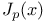 87Ч88 87Ч88
Bessel functions of order  217 217
Bessel functions of order n 80Ч88 217Ч19
Bessel functions of order zero 69Ч80 216 219
Bessel series 79Ч80 83Ч84 109Ч114 138Ч141 216
Birkhoff, G.D. 90 229
Bocher, M. 24 229
Boundary value problems 88Ч90 91Ч141 220Ч223
Bounds of Legendre polynomials 61Ч63
Bounds of normalized Jacobi polynomials 191Ч92 200Ч201
Bounds of other orthonormal polynomials 201Ч208
Broken-line function 13Ч14 21
Byerly, W.E. 112 220
Carslaw, H.S. 229
Charlier, C 178 179
Christoffel Ч Darboux identity 157Ч58
Christoffel, E.B. 54 55 157 158 206
ChristoffelТs identity 54Ч55
Churchill, R.V. 229
Convergence of Fourier series 12Ч14 18Ч25 42Ч44
Convergence of of Legendre series 63Ч68 215
Convergence of of more general series of orthogonal polynomials 191Ч208
Cosine series 6Ч7 8Ч9
Cosine sum 36
Courant, R. 88 189 229
Cylindrical coordinates 106 109Ч114 138Ч141
Damped vibrations 100Ч101 221
Darboux, G. 157 158 175 206 229
de la Valine Poussin, C.J. 35
de Moivre, A. 126
Derivative formula for Hermite polynomials 176Ч77
Derivative formula for Jacobi polynomials 166Ч167
Derivative formula for Laguerre polynomials 184
Derivative formula for Legendre polynomials 57Ч58
Differential equation for 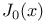 69Ч71 74Ч76 89 219 69Ч71 74Ч76 89 219
Differential equation for 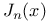 80Ч82 80Ч82
Differential equation for a class of orthogonal polynomials 161Ч165
Differential equation for derivatives of Legendre polynomials 119Ч120
Differential equation for Hermite polynomials 180 226
Differential equation for Jacobi polynomials 173Ч174 225
Differential equation for Laguerre polynomials 186 226Ч227
Differential equation for Legendre polynomials 48Ч49 55Ч57 88Ч89
Differential equation for Pearson frequency functions 142Ч147
Differential equation for sines and cosines 88
Differential equation for Sturm Ч Liouville functions 89Ч90
Discontinuities 9Ч11 22Ч24 65Ч67
Double Fourier series 115Ч117
Elderton, W.Palin 229
Even function 6Ч7
Fejer, L. 32 229
FejerТs theorem 32Ч35
Finite jump 19
Flow of heat 92
for polynomial approximation 212
Fourier series 1Ч44 91Ч101 103Ч105 111Ч112 115Ч117 209Ч211
Frank, P. 230
Frequency functions 142Ч148 223
Function (general notion) 10
Gauss, K.F. 55
Generating function for Hermite polynomials 181
Generating function for Jacobi polynomials 174Ч75
Generating function for Laguerre polynomials 187Ч188
Generating function for Legendre polynomials 45Ч46
Generating function for ultraspherical polynomials 225Ч26
Gibbs phenomenon 24
Gibbs, T.Willard 24
Gram Ч Charlier series 179
Gram, J.P. 178 179
Gray, A. 229
Green, G. 103 107
Harmonic polynomials 126Ч132 137Ч138
Heine, E. 175
Hermite polynomials 176Ч183 226
Hermite series 178Ч179
Hilbert, D. 88 189 229
Hille, E. 230
Hobson, E.W. 229
Ince, E.L. 90 229
Integrability 5
Integrability in the sense of Lebesgue 5 197Ч99
Integral representation of 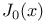 74Ч76 74Ч76
Integral representation of 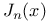 84Ч85 218 84Ч85 218
Integral representation of 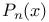 58Ч60 58Ч60
Jackson, D. 44
Jacobi polynomials 166Ч175 200Ч201 225Ч226
Jacobi series 172 201
Kaczmarz, S. 229
Kellogg, O.D. 229
Korous, J. 205
Laguerre polynomials 184Ч190 226Ч227
Laguerre series 186
Laplace series 121Ч138 222
LaplaceТs equation 91Ч96 101Ч112 115Ч141 220Ч222
Leading coefficients of Hermite polynomials 177
Leading coefficients of Jacobi polynomials 169Ч171 172
Leading coefficients of Laguerre polynomials 184
Leading coefficients of Legendre polynomials 47Ч48
Least-square property of Fourier series 27Ч29
Least-square property of general orthogonal polynomials 160Ч161
Least-square property of Legendre series 215Ч216
Lebesgue constants 40Ч42
| Lebesgue, H. 5 40 41 42 43 44 196 197 229
Legendre polynomials 45Ч68 213Ч216
Legendre series 53 63Ч68 107Ч209 214Ч16
Leibniz, G.W. 166 167 169 184 186 187
Liouville, J. 89
Lipschitz, R. 44
Mac Lane, S. viii
Maclaurin, C. 49
MacRobert, T.M. 229
Marden, M. 162
Mathews, G.B. 229
Moments 144Ч48
Moore, C.N. 84
Normalizing factor for Bessel functions 73Ч74 83
Normalizing factor for derivatives of Legendre polynomials 124Ч125
Normalizing factor for Hermite polynomials 177Ч178
Normalizing factor for Jacobi polynomials 171Ч172
Normalizing factor for Laguerre polynomials 185
Normalizing factor for Legendre polynomials 51Ч52
Odd function 7
Orthogonal polynomials 45Ч68 123Ч125 149Ч208 213Ч216 223Ч228
Orthogonality 3 224
Orthogonality, of Bessel functions 71Ч73 82Ч84
Orthogonality, of functions of two variables 117 122Ч124 140
Orthogonality, of Hermite polynomials 177 226
Orthogonality, of Jacobi polynomials 167Ч168
Orthogonality, of Laguerre polynomials 184Ч185 227
Orthogonality, of Legendre polynomials 50Ч51
Orthogonality, of sines and cosines 2Ч3
Orthonormal functions 152
Orthonormal polynomials 154
Parseval, M.A. 29 31 216
ParsevalТs theorem 29Ч31
Pearson, K. 142 147 162 165 230
Peebles, G. 203
Period 1
Po1ya, G. 230
Poisson, S.D. 103 105 136 137
PoissonТs integral 105 136Ч37
Polar coordinates 101Ч103
Probability integral 178
Recurrence formulas for Bessel functions 85Ч87 218
Recurrence formulas for general orthogonal polynomials 156Ч157
Recurrence formulas for Hermite polynomials 179Ч180
Recurrence formulas for Jacobi polynomials 172Ч173
Recurrence formulas for Laguerre polynomials 186Ч187
Recurrence formulas for Legendre polynomials 46Ч47 58Ч60
Recurrence formulas for sines and cosines 211Ч212 225
Riemann Ч Weber 230
Riemann, B. 14 16 21 25
RiemannТs theorem 14Ч16
Rietz, H.L. 230
Robertson, H.P. 230
Rodrigues, O. 57 166 167
RodriguesТs formula 57Ч58
Rolle, M. 78
Schmidt, E. 151 152 224 225
SchmidtТs process of orthogonalization 151Ч153
Schrbdinger equation 181Ч183 188Ч190
Schrodinger, E. 182 188
Schwarz, H.A. 38 39 195 202 204 207 215 224 228
SchwarzТs inequality 38 224
Shohat, J. 230
Sine series 7 8Ч10 94 95 98Ч99 100 101 112
Singular points of differential equations 70 88Ч89
Spherical coordinates 106Ч109 118Ч120 189
Spherical harmonics 118Ч138 189
Steinhaus, H. 229
Stone, M.H. 230
Sturm Ч Liouville boundary value problem 89Ч90
Sturm, C. 89
Summation of series 31Ч35
Szego, G. 174 205 230
Taylor, B. 78
Tchebichef, P.L. 150 230
Titchmarsh, E.C 230
Tonelli, L. 230
Transformation of LaplaceТs equation 101Ч103 105Ч107 129Ч131
Trigonometric sum 25Ч26
Ultraspherical polynomials 225Ч226
Uniform convergence 21Ч22 42Ч44 215
Uspensky, J.V. 230
Van der Waerden, B.L. 189 230
Vibrating membrane 112Ч114 221 222Ч223
Vibrating string 96Ч101 220Ч221
von Mises, R. 230
Walsh, J.L. 230
Watson, G.N. 230
Wave equation of hydrogen atom 188Ч190
Wave equation of linear oscillator 181Ч183
Weierstrass, K. 25 26 32 35 40 137 212 216 227
WeierstrassТs theorem for trigonometric approximation 25Ч27 35Ч40
Weight function 72 149Ч150 153Ч154
Weight function for Hermite polynomials 176
Weight function for Jacobi polynomials 166
Weight function for Laguerre polynomials 184
Weyl, H. 183 189 230
Whittaker, E.T. 230
Zeros of Bessel functions 72Ч73 76Ч79 82 87 218 219
Zeros of general orthogonal polynomials 159Ч160
Zeros of Legendre polynomials 52Ч53
Zygmund, A. 24 230
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте