јвторизаци€
ѕоиск по указател€м
Milewski E.G. Ч Topology Problem Solver
ќбсудите книгу на научном форуме Ќашли опечатку?
Ќазвание: Topology Problem Solverјвтор: Milewski E.G. јннотаци€: Thorough coverage is given to the fundamental concepts of topology, axiomatic set theory, mappings, cardinal numbers, ordinal numbers, metric spaces, topological spaces, separation axioms, Cartesian products, the elements of homotopy theory, and other topics. A comprehensive study aid for the graduate student and beyond.
язык: –убрика: ћатематика /—татус предметного указател€: √отов указатель с номерами страниц ed2k: ed2k stats »здание: 1st edition√од издани€: 1994 оличество страниц: 744ƒобавлена в каталог: 05.04.2008ќперации: ѕоложить на полку |
—копировать ссылку дл€ форума | —копировать ID
ѕредметный указатель
11Ч38 11Ч39 11Ч41 10Ч2 13Ч1 13Ч2 12Ч34 13Ч3 13Ч4 13Ч5 13Ч6 13Ч7 12Ч34 13Ч8 13Ч9 13Ч10 13Ч11 13Ч12 13Ч13 13Ч18 13Ч19 13Ч20 13Ч21 13Ч26 13Ч27 13Ч28 Absorption, law 1Ч10 Adding of handles 9Ч105 Additive families 4Ч19 4Ч20 4Ч21 Affine geometry 9Ч7 9Ч8 £Ч9 Alexandroff compactification 16Ч50 16Ч51 AND, OR, INVERTER gates 1Ч13 1Ч14 Aristotelian logic 1Ч2 Axiom of Choice 7Ч1 Axiomatic formulation 6Ч2 Axiomatic formulation, Axiom of choice 3Ч26 Axiomatic set theory 2Ч24 Baire's category theorem 18Ч39 Basis, properties 11Ч15 11Ч16 11Ч22 11Ч23 11Ч24 Boolean algebra 2Ч25 Borel sets 11Ч42 11Ч43 11Ч44 Boundary 11Ч35 Bounded sets and bounded functions 10Ч26 Brower's fixed point theorem 9Ч88 9Ч89 9Ч90 Burali-forti paradox 8Ч41 Canonical mapping (projection) 3Ч23 Cantor's theorem 18Ч18 Cantor's theorem, Cardinal number of a power set 6Ч10 6Ч11 6Ч12 6Ч13 Cardinal numbers addition 6Ч14 6Ч15 6Ч17 6Ч18 Cardinal numbers exponentiation 6Ч23 6Ч24 6Ч25 6Ч26 6Ч27 6Ч28 Cardinal numbers product 6Ч16 6Ч17 6Ч18 6Ч19 6Ч20 6Ч21 6Ч22 Cardinal numbers, cardinal numbers 5Ч4 Cartesian product 3Ч5 Cartesian product, countable sets 5Ч9 Cartesian product, general cartesian products 4Ч28 4Ч29 4Ч30 4Ч31 14Ч12 14Ч13 Cartesian product, invariants 14Ч7 14Ч8 Cartesian product, metric spaces 10Ч6 14Ч16 14Ч17 Cartesian product, projections 14Ч1 14Ч2 14Ч3 14Ч4 14Ч5 14Ч6 Cartesian product, properties 3Ч6 3Ч7 3Ч8 Cauchy space, Cauchy sequence 18Ч6 18Ч7 18Ч8 18Ч9 18Ч10 18Ч11 18Ч12 18Ч13 18Ч14 18Ч27 18Ч28 Chain 7Ч10 Characteristic function 4Ч25 Chromatic numbers, Color problems, chromatic numbers 9Ч69 9Ч78 9Ч79 Chromatic numbers, Color problems, five color theorem 9Ч80 Chromatic numbers, Color problems, four color problem 9Ч71 9Ч81 Chromatic numbers, Color problems, problem of five regions 9Ч68 Chromatic numbers, Color problems, regular maps 9Ч70 9Ч72 9Ч74 9Ч75 9Ч76 Chromatic numbers, Color problems, seven color theorem 9Ч77 Chromatic numbers, Color problems, six color theorem 9Ч73 Clausius law 1Ч6 Closed ball 10Ч14 Closed sets 10Ч14 10Ч15 10Ч16 10Ч29 10Ч30 10Ч31 Closure, closure of A 10Ч32 Closure, closure of a set 11Ч27 Closure, properties 11Ч28 11Ч29 11Ч30 Cluster point, Derived set 11Ч31 11Ч32 11Ч33 Compact spaces 16Ч1 16Ч2 16Ч3 16Ч4 16Ч5 16Ч7 Compact spaces, countable 16Ч26 16Ч27 Compact spaces, locally 16Ч32 16Ч33 16Ч34 16Ч37 Compact spaces, locally compact Hausdorff spaces 16Ч35 16Ч36 Compact spaces, new 16Ч18 16Ч20 16Ч23 Compact spaces, properties 16Ч8 16Ч9 16Ч11 Compact spaces, sequentially 16Ч24 16Ч25 Compact spaces, sequentially and countable properties 16Ч28 16Ч29 16Ч30 16Ч31 Compactifications 16Ч48 16Ч49 Compactness, compactness in metric spaces 16Ч44 16Ч45 16Ч46 16Ч47 Compactness, compactness of Hausdorff spaces 16Ч12 16Ч13 16Ч14 components 17Ч29 17Ч30 Components theorems 17Ч31 17Ч32 17Ч33 Congruence classes, affine geometry 9Ч7 9Ч8 9Ч9 Congruence classes, congruence 9Ч4 9Ч5 9Ч6 Congruence classes, isometric transformations 9Ч3 Congruence classes, projective geometry 9Ч10 9Ч11 Congruence classes, rigid transformations 9Ч1 9Ч2 Congruence classes, topology 9Ч12 9Ч13 9Ч14 Connected and disconnected spaces 17Ч1 17Ч2 Connected and disconnected spaces, connected subsets of 17Ч9 17Ч13 Connected and disconnected spaces, connected subspaces 17Ч25 17Ч26 17Ч27 17Ч28 Connected and disconnected spaces, locally connected spaces 17Ч39 17Ч40 17Ч42 17Ч43 Connected and disconnected spaces, locally connected spaces, product 17Ч41 17Ч44 Connected and disconnected spaces, product 17Ч34 17Ч35 Connected and disconnected spaces, properties 17Ч3 17Ч4 17Ч5 Connected and disconnected spaces, totally disconnected spaces 17Ч36 17Ч37 17Ч38 Connected networks 9Ч55 Connected surfaces, homotopy classes 9Ч27 Connected surfaces, rank 9Ч28 Connected surfaces, simply connected surfaces 9Ч23 9Ч24 9Ч25 9Ч26 Constituents 2Ч15 2Ч16 Continuity 12Ч1 Continuity at a point, continuity of a point 12Ч18 12Ч19 12Ч20 Continuity at a point, sequential continuity 12Ч21 Continuity of maps 14Ч14 14Ч15 Continuity, applications 12Ч15 12Ч16 12Ч17 Continuity, examples of continuous functions 12Ч2 12Ч3 12Ч5 Continuity, properties of continuous functions 12Ч4 12Ч11 Continuity, sequential continuity 12Ч21 Continuity, theorems 12Ч6 12Ч7 12Ч18 12Ч9 12Ч10 12Ч12 12Ч13 12Ч14 Continuous functions 10Ч21 16Ч6 Continuous functions, examples 12Ч2 12Ч3 12Ч5 Continuous functions, properties 10Ч22 10Ч23 10Ч24 10Ч25 12Ч4 12Ч11 Continuum 17Ч45 17Ч46 17Ч47 17Ч48 Continuum Hypothesis 6Ч40 6Ч41 Contract mapping 18Ч24 Contraposition 1Ч6 Convergence 10Ч17 10Ч19 Convex subsets of 17Ч18 17Ч20 Coverings of space 12Ч23 Coverings, Partitions 4Ч15 4Ч16 4Ч17 4Ч18 Cross-cap 9Ч109 9Ч110 CURVES 9Ч15 9Ч16 9Ч17 d-ball 10Ч7 10Ч8 DeMorgan's laws 1Ч3 1Ч4 DeMorgan's Theorem 2Ч13 2Ч14 Dense and isometric 18Ч33 18Ч34 18Ч36 18Ч37 18Ч38 Dense sets 11Ч36 Denumerable and countable sets, properties 5Ч12 5Ч13 5Ч14 5Ч15 5Ч16 5Ч18 5Ч19 5Ч20 5Ч21 Denumerable sets 5Ч4 5Ч5 5Ч10 Design of circuits 1Ч13 1Ч14 1Ч16 Diagonal 14Ч9 14Ч10 14Ч11 Diagonal, inverse relations 3Ч14 Diameter of a set 10Ч26 10Ч28 Digital systems, AND, OR, INVERTER, gates 1Ч13 1Ч14 Digital systems, design of circuits 1Ч13 1Ч14 1Ч16 Digital systems, logic gates and Boolean algebra 1Ч12 Digital systems, NOR, NAND, gates 1Ч15 Digital systems, TTL ICs 1Ч16 Discrete topology 11Ч10 Duns Scotus law 1Ч6 Equal sets 2Ч2 Equivalence, class 3Ч21 3Ч22 19Ч14 19Ч15 19Ч16 19Ч17 19Ч18 19Ч20 Equivalence, equivalent bases 11Ч25 Equivalence, equivalent sets 5Ч1 5Ч2 5Ч22 5Ч23 5Ч24 Equivalence, equivalent statements 1Ч5 Equivalence, relation 3Ч17 3Ч18 3Ч19 3Ч20 Euclidean space 10Ч3 Euclidean topology 11Ч3 11Ч12 Euclidean topology, basis 11Ч14 11Ч17 Euler characteristics 9Ч106 9Ч107 9Ч108 Euler characteristics, and plane diagram 9Ч101 Euler characteristics, Euler rule 9Ч29 9Ч30 Euler characteristics, index 9Ч42 9Ч43 9Ч44 9Ч45 9Ч46 Euler characteristics, polyhedra 9Ч33 9Ч34 9Ч35 Euler characteristics, regular divisions 9Ч31 9Ч32 Euler characteristics, relation with genus 9Ч39 9Ч40 Euler characteristics, sinks and sources 9Ч41 Euler characteristics, triangulation method 9Ч36 9Ч37 9Ч38 Euler Rule 9Ч29 9Ч30 Families of sets 3Ч9 4Ч19 Family of closed sets 11Ч11 Finite and transfinite numbers 6Ч8 Finite intersection property 16Ч10 First countable spaces 15Ч3 15Ч4 15Ч5 15Ч6 15Ч7 15Ч8 15Ч9 Five color theorem 9Ч80 Five regions, problem 9Ч68 Fixed point theorems, Brower's fixed point theorem 9Ч88 9Ч89 9Ч90 Fixed point theorems, puzzles 9Ч91 Fixed point theorems, rotation 9Ч87 Fixed point theorems, special cases 9Ч92 9Ч93 9Ч94 9Ч95 Four color problem 9Ч71 9Ч81 Functions, 4Ч13 4Ч14 Functions, composition 4Ч5 4Ч6 4Ч7 4Ч8 functions, domain 4Ч1 Functions, functions separating points 13Ч36 13Ч37 Functions, induced functions 4Ч12 Functions, inverse function 4Ч4 Fundamental group 19Ч22 19Ч23 19Ч24 Genus 9Ч18 9Ч19 Graph, equal functions 4Ч3 Hausdorff maximality principle 7Ч31 7Ч32 Homeomorphic functions 16Ч19 Homeomorphic spaces, examples 12Ч35 12Ч38 12Ч39 Homeomorphic spaces, homeomorphism 12Ч30 12Ч31 Homeomorphic spaces, theorems 12Ч33 12Ч34 12Ч36 12Ч37 Homeomorphic spaces, topological properties 12Ч32 Homotopic functions 19Ч1 19Ч2 19Ч3 19Ч17 Homotopic mappings 19Ч9 Homotopy as an equivalence relation 19Ч4 19Ч5 19Ч12 Homotopy class 19Ч6 19Ч27 Ideals, filters 2Ч21 2Ч22 Identification spaces 12Ч40 Identification spaces, examples 12Ч41 12Ч42 Image, inverse image 4Ч9 4Ч10 Implication 1Ч5 1Ч6 inclusion 2Ч3 Independent sets 2Ч17 Induced metric 18Ч2 18Ч3 Infinite and finite sets 5Ч1 5Ч3 Interior 11Ч34 Isometric transformations 9Ч3 Jordan curve, inside and outside 9Ч82 Jordan curve, Jordan curve theorem 9Ч83 9Ч84 9Ч85 Jordan curve, Kuratowski's lemma 7Ч37 Jordan curve, puzzles 9Ч86 Lattice points 5Ч5 Least upper bound and greatest lower bound 7Ч18 7Ч19 7Ч20 Lebesque number of cover 16Ч38 Lexicographic ordering 8Ч29 8Ч30 8Ч31 Limit of sequence 10Ч17 10Ч18 10Ч20 Limit point 18Ч32 Lindeloef spaces 15Ч14 15Ч15 15Ч16 Logic gates and Boolean algebra 1Ч12 Maximal and minimal elements 7Ч21 7Ч22 7Ч23 7Ч24 Maximal and minimum 7Ч25 7Ч26 7Ч27 Metric spaces, countable 18Ч4 18Ч19 Metric spaces, metric space 10Ч1 10Ч2 10Ч4 10Ч5 15Ч22 15Ч23 15Ч24 15Ч25 15Ч26 Metric spaces, metric space, complete 18Ч15 18Ч16 18Ч17 18Ч20 18Ч21 18Ч22 18Ч23 18Ч26 18Ч29 18Ч30 18Ч35 Metrizable spaces 18Ч1 18Ч5 18Ч31 Moebius band and Klein bottle 9Ч20 9Ч21 9Ч22 9Ч99 Multiplicative families 4Ч19 4Ч20 4Ч21 NbdЧfinite family 12Ч22 Neighborhood, adherent points 11Ч27 Networks, connected networks 9Ч55 Networks, planar and nonplanar networks 9Ч49 9Ч50 9Ч51 Networks, problems and puzzles 9Ч60 9Ч62 9Ч53 9Ч64 9Ч65 9Ч66 9Ч57 Networks, single path 9Ч52 9Ч53 9Ч54 Networks, tieЧsets 9Ч58 Networks, traversing a network 9Ч59 9Ч60 9Ч61 Networks, trees 9Ч56 9Ч57 Networks, vertices 9Ч47 9Ч48 Non-countable spaces 5Ч6 NOR, NAND, gates 1Ч15 Normal spaces 13Ч22 13Ч23 13Ч24 13Ч25 Numbers card N and card R 6Ч1 6Ч3 6Ч4 Open and closed functions 12Ч5 Open and closed functions, example 12Ч27 Open and closed functions, properties 12Ч26 12Ч28 12Ч29 Open covers, refinements 15Ч1 15Ч2 Open sets 10Ч11 10Ч12 10Ч13 Order isomorphism 8Ч1 8Ч2 8Ч3 Ordered pair 3Ч5 Ordered sets 7Ч28 7Ч29 7Ч30 Ordinal numbers 8Ч4 Ordinal numbers, ordering 8Ч5 8Ч6 8Ч7 8Ч8 8Ч9 8Ч10 Ordinal numbers, ordinal number У 8Ч11 8Ч12 Ordinal numbers, product 8Ч28 8Ч32 Ordinal numbers, properties 8Ч24 8Ч25 8Ч26 8Ч27 Ordinal numbers, sum 8Ч14 8Ч15 8Ч16 8Ч17 Partial order 7Ч7 7Ч9 7Ч11 7Ч14 Path connected sets 17Ч14 17Ч15 17Ч16 17Ч17 Path connected sets, properties 17Ч21 17Ч22 17Ч23 Paths, arcs and loops are homotopic 19Ч7 19Ч8 19Ч10 19Ч11 19Ч12 19Ч13 19Ч21 Piecewise definition of maps 12Ч24 Piecewise definition of maps, coverings of space 12Ч23 Piecewise definition of maps, Nbd-finite family 12Ч22 Planar and nonЧplanar networks 9Ч49 9Ч50 9Ч51 Plane diagrams 9Ч96 9Ч97 9Ч98 Plane diagrams, Euler characteristic and plane diagram 9Ч101 Plane diagrams, Moebius band and Klein bottle 9Ч99 Plane diagrams, real projective plane 9Ч100 Plane diagrams, seven color theorem 9Ч102 Plane diagrams, symbolic representation 9Ч103 Polygonally connected sets 17Ч14 17Ч19 Polyhedra 9Ч33 9Ч34 9Ч35 Power sets 2Ч8 2Ч9 5Ч17 Preorder 7Ч4 7Ч5 7Ч6 Principle of transfinite induction 7Ч48 7Ч49 Product, properties 8Ч33 8Ч34 8Ч35 8Ч36 8Ч37 Projective geometry 9Ч10 9Ч11 Quantifiers 3Ч2 3Ч3 3Ч4 Rank 9Ч28 Real projective plane 9Ч100 Real-valued functions 4Ч24 Regular divisions 9Ч31 9Ч32 Regular maps 9Ч70 9Ч72 9Ч74 9Ч75 9Ч76 Regular spaces 13Ч14 13Ч15 13Ч16 13Ч17 Regular spaces, complete 13Ч38 13Ч39 Relation with genus 9Ч39 9Ч40 Relation-preserving functions 4Ч26 4Ч27 Relations 3Ч13 Relations, composition 3Ч15 3Ч16 Remarks 8Ч38 8Ч39 8Ч40 Restriction, extension 4Ч3 Rigid transformations 9Ч1 9Ч2 Rings 2Ч20 Rotation 9Ч87 Russell paradox 2Ч23 Second countable spaces 15Ч10 15Ч11 15Ч13 segments 7Ч44 7Ч45 7Ч46 7Ч47 Sentence functions of two variables 3Ч24 3Ч25 Sentences, sum, product, negation 1Ч1 Separable spaces 15Ч12 15Ч17 15Ч18 15Ч19 15Ч20 15Ч21 Separated sets 17Ч6 Sequences 10Ч17 Sequential continuity 12Ч21 Set 10Ч27 Set of, algebraic numbers 5Ч11 Set of, functions 4Ч22 4Ч23 Set of, operations 2Ч4 2Ч5 2Ч6 2Ч7 Set of, rational numbers 5Ч5 Set of, real numbers 5Ч6 Sets, elements 2Ч1 Seven color theorem 9Ч77 9Ч102 Shroeder Ч Bernstein theorem, ordering of cardinal numbers 6Ч5 6Ч6 6Ч7 6Ч9 Simple chain 17Ч24 Simply connected surfaces 9Ч23 9Ч24 9Ч25 9Ч26 Single path 9Ч52 9Ч53 9Ч54 Sinks and sources 9Ч41 Six color theorem 9Ч73
–еклама
 |
|
ќ проекте
|
|
ќ проекте



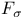 and
and 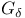 sets
sets 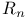 space
space 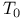 Чspaces
Чspaces 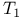 -spaces
-spaces 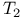 Чspaces
Чspaces 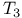 Чspaces
Чspaces 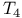 Чspaces
Чspaces 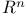
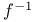 , properties
, properties  Ф
Ф 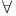 and
and