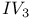|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Bliss G.A. — Lectures on the Calculus of Variations |
|
|
 |
| Предметный указатель |
Accessory minimum problems and differential equations 27 55 84 89 118 228 229
Accessory minimum problems and differential equations, canonical accessory equations 135 229
Accessory minimum problems and differential equations, conjugate systems of solutions 233
Admissible sets of variables and arcs 7 66 133 194
Admissible variations 195
Auxiliary theorems for the problem in 3-space 18 38
Auxiliary theorems for the problem of Bolza 237
bernoulli 4 147
BLISS 13 16 54 60 147 187 219 260 264 269
Bolza v 43 147 157 187 188 219 269
Boundary value problems 260
Canonical variables and equations 65 92 132 207 209
Canonical variables and equations for second variation 134 229
Caratheodory 77 188
Characteristic numbers and sets 261
Clebsch 187 219 220
Clebsch, his necessary condition III for the problem of Bolza 224
Conjugate points 28 84 253
Conjugate points, determination of 32 88 119 259
Conjugate points, geometric interpretation 34
Conjugate points, two definitions 26 28
Conjugate systems of solutions of the accessory equations 233
Cope 187
Curves of quickest descent 78
Darboux 24
Elementary family of arcs 194
Envelope theorems 24 25 88
Envelope theorems for parametric problems 116
Equivalence of problems 189
Erdman, corner condition 12 203
Euler 37
Euler, differential equations 12 82 87 111 203
examples v
Examples, brachistochrone problem 4
Examples, shortest distance problem 3
Examples, the integral of the special relativity theory 8
Existence theorems for differential equations 274 276
Existence theorems for differential equations, derivatives of solutions with respect to constants of integration 278 281 282
Existence theorems for differential equations, the imbedding theorem 277
Extremals 15 111 207
Extremals as characteristics of the Hamilton — Jacobi equation 73
Extremals of a field 45 51 125 238
Extremals, non-singular 15 207
Fields of extremals 44 124 237
Fields of extremals, method of constructing 46 237
Focal points for general problems with one end-point variable 170
Focal points of a surface in 3-space 150
Focal points, dependence of focal points upon curvature 175
Fundamental formula related to second variation 59 99
Fundamental lemma 10
Galileo 3
Goldstine vi 7 148 170 257
Graves vi 43 147 188 219
Hahn 7 219
Hahn, theorem of Hahn 159
Hamilton 65 67 81 92
Hamilton, construction of a complete integral 141
Hamilton, the Hamilton — Jacobi partial differential equation 71 94 138
Hestenes vi 41 147 148 187 188 264
Hilbert, differentiability condition 13 204
| hu 187
Imbedding lemma 196 198
Imbedding theorems for an admissible arc in a family of such arcs 196 198
Imbedding theorems for differential equations in general 277
Imbedding theorems for parametric problems 112
Imbedding theorems for problem of Bolza 208
Imbedding theorems for problems in 3-space 16 68
Implicit function theorems 270 272
Integrals independent of the path of integration 49
jacobi 37 65 67 81 92 147
Jacobi, condition IV for other problems 83 88 116
Jacobi, differential equations 27
Jacobi, his necessary condition IV for the problem in 3-space 26 27
Kneser 147
Lagrange 187 188
legendre 23 37
Levi 54
Malnate 54
Mayer 37 187 188 219
McShane vi 187 188 219
Morse vi 157 187 188 219
Multiplier rule 202
Myers, F.G. 188
Myers, S.B. 187 219
Non-tangency condition 192
Normality for minima of functions of a finite number of variables 210
Normality for the problem of Bolza 213
Normality on an interval 218
Notations for conditions, 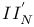 41 127 235 41 127 235
Notations for conditions, 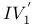 , , 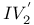 , , 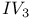 257 263 257 263
Notations for conditions, I, II, III 11 22 87 108 235
Notations for conditions, IV 26 83 88 117 165 235
Notations for conditions, primed conditions 40 127 166 235
Parametric problems 102
Parametric problems, fundamental properties of their integrands 106
Parametric problems, their integrals 104
Reid vi 41 43 54 188 219
Schoenberg 187
Separated end-conditions 191
Slope functions of a family of extremals 38
Slope functions of a field 44 51 89 124 237
Sufficiency theorems for abnormal cases of Hestenes 264
Sufficiency theorems for strong relative minima 42 235
Sufficiency theorems for weak relative minima 40 252
Sufficiency theorems without the use of fields 59 62
Sufficiency theorems, fundamental sufficiency theorems 46 125 241 247
Sufficiency theorems, table of necessary and of sufficient conditions for a minimum 43 132
Transversality 25 149 162 202
Transversality, transversal surface 49
Variations 6
Variations, equations of variation 194
Variations, first and second variations 10 84 97 199 226 243
Variations, positive definite second variation 227
Variations` of an admissible family of arcs 195
Von Escherich 219
Weierstrass 37 41 43 54 220
Weierstrass, corner condition 12 82
Weierstrass, his integral formula 45 56 125 241
Weierstrass, his necessary condition II 22 83 109 223
Zermelo 24
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



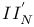
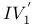 ,
, 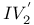 ,
,