|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Takeuti G., Zaring W.M. — Introduction to Axiomatic Set Theory |
|
|
 |
| Предметный указатель |
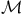 -constructible 140 -constructible 140
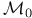 -definable 201 -definable 201
Absoluteness 112—123
Addition, ordinal 49
Aleph Hypothesis (AH) 93 96
Almost universal 135
Arithmetic, ordinal 49—62
Auxiliary symbols 4 236
axiom of abstraction 9 16
Axiom of Choice (AC) 2 87 87—101
Axiom of constructibility 152—174
Axiom of extensionality 7 123
Axiom of foundation 18
Axiom of infinity 39 123 129
Axiom of pairing 14 123—126
Axiom of Powers 15 123 127—128
Axiom of regularity 18 19 130
Axiom of unions 15 123 126—127
Axiom, schema of replacement 17 128
Axiom, Schema of Separation 16—17
Axioms, logical 5
Benacerraf, Paul 2
Bernays, Paul (1888) 3
Bernstein, Felix 71
Burali — Forti paradox 37
Cantor — Schroder — Bernstein Theorem 71 90
Cantor, Georg (1845—1918) 1—3 32 37 71—73 88 90 92
Cantor’s Law of Trichotomy 88
Cantor’s Law of Trichotomy, notion of cardinal number 73
Cantor’s Law of Trichotomy, notion of ordinal number 32
Cantor’s Law of Trichotomy, notion of set 2
Cardinal, inaccessible 85—86
Cardinal, numbers 1 71—101
Cardinal, numbers, Cantor’s notion of 73
Cardinal, numbers, class of 79
Cardinal, numbers, cofinality of 82
Cardinal, regular 85
Cardinal, singular 85
Cardinal, weakly inaccessible 85—86
Character of cofinality 84
Class of cardinal numbers 79
Class of closed limited formulas 191
Class of closed wffs 191
Class of limit ordinals 38
Class of prime formulas 178
Class of quasi formulas 179
Class of statements 203
Class of wffs 189
Class(es) 3 9—20
Class(es), ordinal 32
Class, almost universal 135
Class, definable 237
Class, M-constructible 140
Class, proper 3 12
Class, symbol 9
Closed limited formulas 190—191
Closed limited formulas, unlimited statements 203
Closed limited formulas, wffs 190—191
Cofinality of ordinals 82
Cofinality, character of 84
Cohen, Paul 2 3 73 96
Complete sequence of forcing conditions 210
Conjunction 4
Constant, predicate 4
Continuum Hypothesis (CH) 2 92
Dedekind, Richard (1831—1916) 1 2
Definable class 237
Definable class, set 13
Disjunction 4
End of string 184
Equality 6—8
EQUIVALENCE 4
Equivalence, of sets 71
Equivalent, logically 5
Existential quantification 4
Extensionality 7—8
Finite induction 39
Finite induction, recursion 43
Finite induction, set 75
Forcing conditions 204
Forcing conditions for unlimited statements 205
Forcing conditions, complete sequence of 210
Forcing conditions, for limited statements 205—206
Forcing set 211
Formula, model of 103
Formula, parity of 204
Formula, quasi 179
Formula, quasi limited 179
Formula, subquasi 187
Formula, type of 203
Formula, unlimited 203
Formula, well formed 4 175 189 237
Formulas, logically equivalent 5
Formulas, prime 5 178
Formulas, well formed 4
Formulas, well formed parts of 5
Foundational relation(s) 27
Fraenkel, Abraham A. (1891) 3 16 17
Frege, Gottleb (1848—1925) 1 2 32 73
Function(s) 21—31
Function, ordinal 44
Function, satisfaction 192
Fundamental function 214
Fundamental function, operations 133
Generalized Continuum Hypothesis (GCH) 2 92—100
Godel — Bernays model 148—174
Godel — Bernays numbers 176
Godel — Bernays set theory (GB) 3
Godel — Bernays, Kurt (1906) 2 3
Implication 4
Inaccessible cardinal 85—86
Individual variables 4
Induction, finite 39
Induction, transfinite 35
Inference, rules of 5
Infinite set 75
J-function 228
Konig 100
Language(s) 4—5 236—238
Limit ordinal 37
Limit ordinals, class of 38
Limited quantifier 178
Limited statements, forcing for 205
Lindenbaum, A. 93
Logic 4—5
Logical axioms 5
Logical symbols 4
Logically equivalent 5
membership 3
Minimal model 197
Model of a formula 103
| Model of ZF 102 130—142
Model, minimal 197
Model, standard transitive 107
Models 102—111
Montague, Richard 17
Mostowski, A. 107
Multiplication, ordinal 53
n-tuple, ordered 14
n-tuple, unordered 14
Negation 4
Number(s), cardinal 1 71—86
Number(s), ordinal 1
Order of a set 149
Order, partial 26
Order, relation 26
Ordered n-tuples 14
Ordered pairs 14
Ordinal addition 49
Ordinal arithmetic 49—62
Ordinal classes 32
Ordinal function 44
Ordinal multiplication 53
Ordinal numbers 1 32—62
Ordinal numbers, Cantor’s notion of 32
Ordinal, limit 37
Ordinals, cofinality of 82
Pair, ordered 14
Pair, unordered 14
Paradox, Berali-Forti 37
Paradox, Russell’s 2 9 10
Parity of a formula 204
Partial ordering 26
Peano postulates 38
Poincare, Henri (1854—1912) 47
Power set 15
Predicate constant 4
Predicate symbol 3
Prime formulas 5 178
Proper class (s) 3 12
Putnam, Hilary 2
Quantification, existential 4
Quantification, limited 178
Quantification, universal 4
Quasi formulas 179
Quasi formulas, string of 182
Quasi limited formulas 179
Quine, Van Orman 8
R-minimal element 27
Rank 66 68
Recursion, finite 43
Recursion, transfinite 42
Regular cardinal 85
Relational systems 26—31 102
Relations 21—31
Relations, foundational 27
Relations, order 26
Relations, well founded 27
Relations, well ordering 27
Rubin, H. 96
Rules for well formed formulas 4
Rules of Inference 5
Russell class 13
Russell, Bertrand (1872—1970) 1—3 9 32 73
Russell’s paradox 2 9 10
Satisfaction functions 192
Schroder, Ernst 71
Scott, Dana 8
Set theory, Godel — Bernays (GB) 3
Set theory, Zermelo — Fraenkel (ZF) 3 5 9
Set(s) 3 12
Set(s), Cantor’s notion of 2
Set, definable 13
Set, finite 75
Set, forcing 211
Set, infinite 75
Set, order of 149
Set, power 15
Set, supertransitive 66
Set, transitive 32
Set, union 15
Set, well founded 67
Sets, equivalent 71
Sierpinski, W. 93—94
Singular cardinal 85
Skolem, Thoralf (1887—1963) 3
Standard Model Hypothesis 197
Standard structure 103
Standard transitive model 107
statements 203
Statements, class of 203
String of quasi formulas 182
String, end of 184
Structure 102
Structure, standard 103
subclass 15
Subquasi formula 187
Supertransitive set 66
Symbol(s), logical 4
Symbol(s), predicate 4
Symbol, class 9
Symbols, auxiliary 4 236
Symbols, logical 4
Tarski, A. 93
Term 12 236
Theory of types 3
Transfinite induction 35
Transfinite recursion 42
Transitive set 32
Type of a formula 203
Types, theory of 3
Union, of a set 15
Universal quantification 4
Unlimited formulas 203
Unlimited statements 203
Unlimited statements, forcing for 205
Unordered n-tuple 14
Unordered pair(s) 14
van Heijenoort, Jean 2
Variables, individual 4
von Neumann, John (1903—1957) 3 32
Weakly inaccessible cardinals 85—86
Well formed formulas 4 175 189 237
Well formed formulas in the wider sense 10
Well formed formulas, rules for 4
Well founded relation(s) 27
Well founded set 67
Well Ordering Principle 88
Well ordering relations 27
Whitehead, Alfred North (1861—1947) 3
Zermelo — Fraenkel set theory (ZF) 3 5 9
Zermelo, Ernst (1871—1953) 1 3 16—18 98
Zorn’s Lemma 88
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



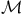 -constructible
-constructible 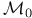 -definable
-definable