|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Gilmore R. — Lie Groups, Lie Algebras and Some of Their Applications |
|
|
 |
| Предметный указатель |
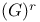 29 29
 29 29
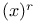 33 33
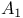 281 283 284 291 307 314 317 281 283 284 291 307 314 317
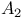 281 283 284 285 291 307 281 283 284 285 291 307
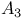 350 350
 13 19 13 19
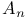 278 285 293 298—300 305 306 310 315 316 324 326 339 347 348 360 505 278 285 293 298—300 305 306 310 315 316 324 326 339 347 348 360 505
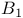 281 291 314 281 291 314
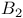 283 291 307 314 376 283 291 307 314 376
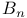 278 285 294—300 305 306 310 311 315 316 324 326 342 347 360 505 278 285 294—300 305 306 310 311 315 316 324 326 342 347 360 505
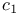 281 291 314 281 291 314
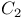 (root space) 283 291 300 307 314 316 (root space) 283 291 300 307 314 316
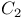 (vector space) 136 147 148 159 179 (vector space) 136 147 148 159 179
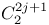 136 140 136 140
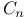 278 285 294—300 305 306 310 311 315 316 324 326 343 347 360 501 505 278 285 294—300 305 306 310 311 315 316 324 326 343 347 360 501 505
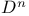 377 378 382 433 377 378 382 433
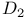 283 284 291 307 283 284 291 307
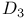 350 350
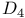 286 287 313 286 287 313
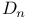 278 285 294—300 305 306 310 311 312 315 316 324 326 343 347 348 360 501 505 278 285 294—300 305 306 310 311 312 315 316 324 326 343 347 348 360 501 505
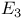 288 289 314 288 289 314
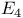 289 291 314 289 291 314
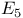 288 289 291 314 288 289 291 314
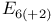 347 361 417 418 347 361 417 418
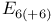 347 361 417 418 347 361 417 418
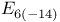 347 361 417 418 347 361 417 418
 347 361 417 418 347 361 417 418
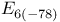 347 417 418 347 417 418
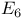 289—291 312—314 325 326 347 361 289—291 312—314 325 326 347 361
 347 361 418 419 347 361 418 419
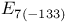 347 418 419 347 418 419
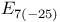 347 361 418 419 347 361 418 419
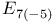 347 361 418 419 347 361 418 419
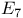 290 291 312—314 317 325 326 347 361 290 291 312—314 317 325 326 347 361
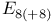 347 361 419 347 361 419
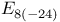 347 361 419 347 361 419
 347 419 347 419
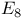 290 291 312—314 317 325 326 347 361 290 291 312—314 317 325 326 347 361
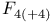 347 361 416 417 347 361 416 417
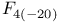 347 361 416 417 491 347 361 416 417 491
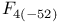 347 416 417 491 347 416 417 491
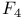 287 291 292 306 311 316 325 326 347 361 491 287 291 292 306 311 316 325 326 347 361 491
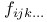 34 35 34 35
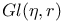 107 114 107 114
 281—286 291 292 307—310 316 317 325 326 347 361 281—286 291 292 307—310 316 317 325 326 347 361
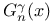 54 54
 347 361 416 347 361 416
 347 416 347 416
 202—205 209 213 370 445 202—205 209 213 370 445
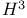 214 214
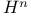 451 453 455 499 451 453 455 499
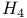 462 463 495 462 463 495
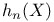 54 54
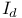 40 40
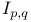 339 340 342—344 339 340 342—344
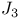 , matrix elements of 140 155 180 , matrix elements of 140 155 180
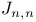 339 340 342 343 339 340 342 343
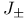 , matrix elements of 139—141 155 180 , matrix elements of 139—141 155 180
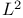 21 54 21 54
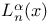 54 54
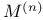 21 21
 12 13 12 13
 45—52 45—52
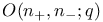 45—52 45—52
 45—52 85 45—52 85
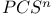 372 372
 371 371
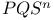 372 372
 311 311
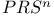 372 372
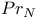 371 371
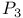 31 32 105 118 31 32 105 118
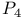 2 11 20 2 11 20
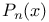 54 54
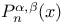 54 54
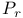 11 31—33 11 31—33
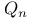 7 49 7 49
 th-order tensor product 29 th-order tensor product 29
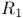 14 15 142 143 14 15 142 143
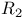 209 210 213 445 478 209 210 213 445 478
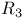 147 148 149 179 147 148 149 179
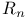 14 49 118 453 455 14 49 118 453 455
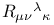 132 132
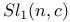 37 48 50 37 48 50
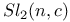 37 48 50 37 48 50
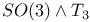 83 83
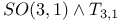 83 83
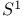 179 328 427 179 328 427
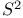 179 202 203 206—209 213 367 370 444 179 202 203 206—209 213 367 370 444
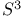 214 214
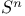 365 368 384—386 388 390 392—394 399 400 427 430 431 450 453 455 499 365 368 384—386 388 390 392—394 399 400 427 430 431 450 453 455 499
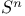 , surface area of 392—393 , surface area of 392—393
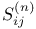 13 13
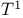 143 143
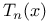 54 54
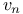 6 14 18 213 6 14 18 213
 6 6
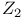 143 200 143 200
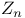 200 200
 function 393 function 393
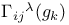 55 55
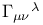 132 132
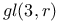 226 227 241 226 227 241
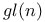 481 482 481 482
 186 352 186 352
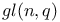 215 215
 186 186
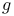 201 213 214 215 201 213 214 215
 505 505
 460 460
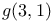 460 460
 456 472 505 456 472 505
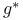 200 201 215 200 201 215
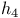 423 461—463 494 495 497 423 461—463 494 495 497
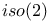 210 444 210 444
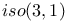 460 460
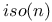 455 459 455 459
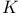 200 201 208 213 214 215 200 201 208 213 214 215
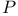 201 202 206 208 213 214 215 201 202 206 208 213 214 215
 200 201 202 204 206 214 215 200 201 202 204 206 214 215
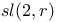 271 271
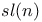 482 482
 37 48 50 185—186 293 340 37 48 50 185—186 293 340
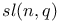 215 215
 186 293 346 186 293 346
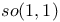 211 211
 205 207 208 210 205 207 208 210
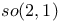 202 205 211 429 430 202 205 211 429 430
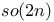 274 276 344 501 274 276 344 501
 118 274 276 278 118 274 276 278
 207 208 214 275 502 207 208 214 275 502
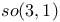 502 502
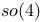 214 214
 429 429
 429 430 429 430
 296—297 296—297
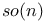 186 193—195 214 451 454 455 459 472 494 186 193—195 214 451 454 455 459 472 494
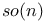 , Cartan — Killing metric on 251 , Cartan — Killing metric on 251
 454 454
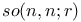 296—297 296—297
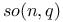 215 215
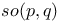 186 276 459 186 276 459
 195 275 344 195 275 344
 296—297 426 501 296—297 426 501
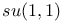 201 203 205 271 201 203 205 271
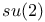 207 208 271 276 317 207 208 271 276 317
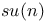 185—186 239 240 274 276 293 340 185—186 239 240 274 276 293 340
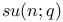 215 215
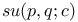 276 293 276 293
| 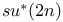 186 215 293 346 186 215 293 346
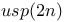 215 276 494 215 276 494
 276 276
 205 207 208 239 205 207 208 239
 494 495 497 494 495 497
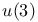 424 424
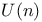 185 186 194 195 214 239 240 274 276 427 494 500 501 185 186 194 195 214 239 240 274 276 427 494 500 501
 185 186 185 186
 141 253 141 253
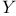 145 146 145 146
 162 162
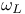 163 164 165 163 164 165
 57 57
 -pulse 163 165—167 176—178 -pulse 163 165—167 176—178
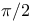 -pulse 163—165 176 177 -pulse 163—165 176 177
 -ordered product 114—117 161 162 -ordered product 114—117 161 162
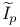 42 339 42 339
1-1 14
1-1 correspondence 2 16
Abelian 3 224 317
Abelian algebra 230—232 274 492
Abelian group 3 5 83 95 118 225
Abelian invariant subalgebra 236 243 268 444 449 453 477 482 484
Abelian invariant subgroup 72 340 342—344 346 424 425
Abelian subgroup 72 362
Abragam, A. 178 181
Abramowitz, M. 435
Accidental degeneracy vi
Action integral 145
Action principle 145
Active interpretation of transformation 66
Ad(g) 83
Addition 2 3
Addition, pointwise 21
Adjacent interchange 11 21 30—32
Adjoint 266 298
Adjoint representation 106 216 218
Ado, I.D. 119
Ado’s theorem 104
Aghassi, J.J. 506
Algebra 8 9 12 13 19
Algebra for orthogonal groups 186 191
Algebra for symplectic groups 188 191
Algebra for unitary groups 185 190
Algebra, associative 9
Algebra, bases for classical 13 182—215
Algebra, direct sum 142
Algebra, irreducible 236
Algebra, linear 8
Algebra, noncompact 200
Algebra, representation for 19 149 158
Algebra, simple 236
Algebraic group 83 85
Algebraic properties, of Lie group 326—334
Algebraic structure 14
Algebraic structure on continuous group 63
Algebraic, equations 241
Algebraically closed 183 241 318
Analytic 77
Analytic continuation 186 192 212 421
Analytic functions 53 70 363 431
Analytic functions, bases for 21 33
Analytic group multiplication 111
Analytic isomorphism 94 107 114 119 151 152
Analytic mapping 114 372
Analytic structure 94
Analytically isomorphic 94
Angular coordinate 432
Angular momentum, orbital 23
Angular momentum, spin 23
Annihilate 242 243
Annihilation operators 423—425 427 461 499—501 505
Annihilation operators for Bosons 499—501 505
Annihilation operators for Fermions 499—501 505
Anomalous magnetic moment 162
Anticommutation 9 22
Anticommutation relations 499
Anticommutator 9
Anticommute 339
Antihermitian matrix 184 185 340 341 343 344 347 350—352
Antinormal order 172 173
Antipodal points 127 128 130
antisymmetric 9
Antisymmetric matrix 9 13 19 186 187 339 342 343 347
Antisymmetric matrix representation, of a group 30—33
Antisymmetric metric 40 41
Antisymmetric subspace 53
Antisymmetric tensor 30—33 259
Antisymmetrization 9
Antiunitary representation v
Apostol, T.M. 56
Arecchi, F.T. 181 506
Associated Legendre polynomials, generating function for 181
Associative algebra 9 219 274 322 492
Associative algebra and Jacobi identity 104?105 491
Associativity 1 3 5 8 9 17 18 68 69 320
Associativity and Jacobi identity 104—105 491
Associativity for continuous group 64
Associativity for continuous group of transformations 65
Asteroid B-612 436 437
Atomic scattering factor 498
Aut 320—323 501
Automorphism 319—339
Automorphism, group 322
B 162 165 166 169
Baiquni, A. 349
Baker — Campbell — Hausdorff formulas 94 119 460—463 497 498 504
Baker — Campbell — Hausdorff formulas for SU(2) 149 152 153 157 168 169 173 179
Baker, G.A. 349 435
Baker, H.F. 119
Ball-box problem 32
Bartee, T.C. 23
Barut, A.O. 349 435
Baryon number 121 146
Bases 7 10—13 18 19 95 see
Bases for algebra 13 212
Bases renormalized 40 41
Basic root 297 298
Basis 7 12 19
Basis for algebra 184—189 294 298
Basis for analytic functions 70
Basis for Gl(n, c) 186
Basis for SO(n, c) 187
Basis for Sp(2n, c) 189
Basis vector 85 105 113 118 see
Basis vector for Lie algebra 217 219
Bateman, H. 349
BCH formulas 119 121 158 302 317 397 401 see
BCH formulas for SU(2) 149 152 153 157 168 169 173 179
BCH formulas on cosets 381
Berezin, F.A. 435
Berger, M. 435
Bessel function 495 496
Bessel, equation 496
beta function 400
Bethe, H.A. 56
Biedenharn, L.C. 277 317
Bilinear 8 12 38
Bilinear antisymmetric metric 187
Bilinear metric, antisymmetric 187
Bilinear metric, symmetric 186
Bilinear metric-preserving quaternion groups 44—45
Bilinear symmetric metric 186
Bilinearity 5
Binomial coefficients 139
Binomial theorem 137
Birkhoff, G. 23
Bishop, R.L. 86
Bloch sphere 170
Bloch state 171
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



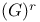

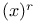
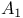
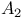
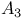

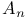
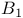
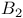
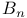
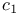
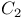 (root space)
(root space) 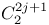
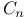
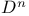
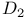
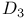
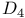
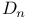
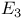
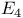
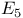
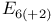
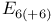
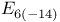

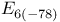
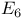

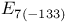
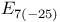
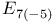
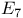
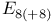
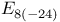

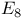
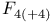
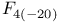
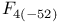
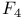
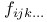
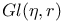

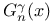



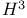
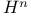
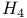
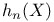
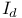
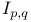
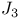 , matrix elements of
, matrix elements of 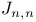
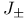 , matrix elements of
, matrix elements of 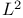
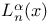





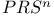
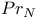
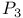
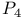
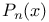
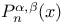
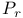
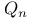
 th-order tensor product
th-order tensor product 
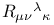
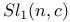
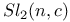
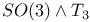
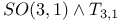
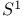
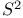
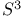
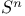
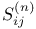
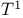
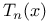
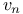

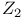
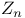
 function
function 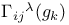
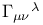
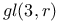
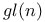

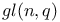





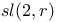

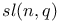

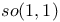

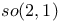
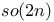


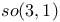
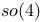



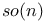

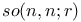
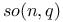


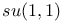
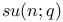
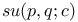
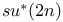
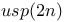



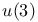




 -pulse
-pulse 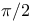 -pulse
-pulse  -ordered product
-ordered product