|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Kollar J. — Rational Curves on Algebraic Varieties |
|
|
 |
| Предметный указатель |
 VI.2.6 p. VI.2.6 p.
 VI.2.6 p. VI.2.6 p.
 , ,  III.1.1 p. III.1.1 p.
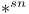 , ,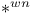 I.7.2.1 p. I.7.2.1 p.
![$*^{[-1]}$](/math_tex/3047feed19ce5b6ff6a3160ebbd5733882.gif) I.3.10 p. I.3.10 p.
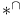 II.4.2.6 p. II.4.2.6 p.
 T.3 p.3 T.3 p.3
 , ,  II.4.1 p.122 II.4.1 p.122
 , , II.3.12 p. II.3.12 p.
 , ,  II.4.1 p.122 II.4.1 p.122
 ( ) IV.4.8 p.212 ( ) IV.4.8 p.212
 , , 1.4.11 p. 1.4.11 p.
 , ,  1.4.11 p. 1.4.11 p.
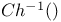 I.3.24.3 p. I.3.25.2 p. I.3.24.3 p. I.3.25.2 p.
 III.1.8 p. III.1.8 p.
 I.3.1 p.41 I.3.1 p.41
 II.3.12 p. II.3.12 p.
 II.3.5.4 p.115 II.3.5.4 p.115
 II.2.6 p. II.2.6 p.
 II.2.15 p. II.2.15 p.
 I.3.24.1 p. I.3.24.1 p.
 II.4.2 p. II.4.2 p.
 , ,  II.4.1 p. II.4.1 p.
 IV.4.10 p. IV.4.10 p.
 I.1.4.1.2 p. I.1.4.1.2 p.
 II.2.11 p. II.2.11 p.
 , ,  II.4.1 p. II.4.1 p.
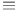 II.4.1.5 p. II.4.1.5 p.
 V.1.3 p. V.1.3 p.
 , ,  II.2.11 p. II.2.11 p.
 , ,  II.4.6 p. II.4.6 p.
 , ,  , , 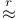 II.4.1 p. II.4.1 p.
 , ,  II.4.1.8 p. II.4.1.8 p.
 IV.4.2 p. IV.4.2 p.
 T.2 p.3 T.2 p.3
Algebraic cycle I.3.1 p.
Algebraic equivalence II.4.1 p.
Algebraic realization IV.4.2 p.
Algebraic relation IV.4.2 p.
Algebraic relation, irreducible IV.4.2 p.
Algebraic relation, open IV.4.2 p.
Algebraic relation, proper IV.4.2 p.
Ample (vector bundle) II.3.8 p. V.3.9 p.
Anticanonical degree II.3.12 p.
Anticanonical ring II.3.3 p.
Attaching trees II.7.4 p.
Aut( ),  I.1.10.2 p. I.1.10.2 p.
Bend-and-break II.5 p.
Big T.1 p.3
Birational transform T.3 p.3
Bundle, 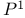 -bungle II.2.5 p. -bungle II.2.5 p.
C Div( ) I.1.12 p.
Canonical ring III.3.3 p.
Cartier divisor, effective I.1.11 p.
Cartier divisor, relative I.1.11 p.
Cayley form I.3.24.1 p.
CDiv( ) I.1.13 p. II.4.2 p.
ch( ) 1.3.24.1 p.
Chain (of smooth rational curves) II.7.4 p.
Chain, rationally chain connected IV.3.2 p.
Chow field I.3.24.1 p.
Chow field condition I.4.7 p.
Chow form I.3.24.1 p.
Chow functor I.3.20 p. I.5.2 p.
Chow pull-back I.3.18 p.
Chow( ) I.3.21 p.
Chow( ), I.3.20 p. I.5.3 p. I.3.20 p. I.5.3 p.
Closed under * IV.2.1 p.
Comb II.7.7 p.
Cone of curves II.4.7 p.
Cone of effective cycles II.4.1.7 p.
Connected by a *-chain IV.4.7 p.
Connected, connected by a *-chain IV.4.7 p.
Connected, rationally chain connected IV.3.2 p.
Connected, rationally connected IV.3.2 p.
Connected, separably rationally connected IV.3.2 p.
Connected, two general points can be connected by a *-chain IV.4.9 p.
Contractible II.5.2 p.
Cycle defined over a subfield I.3.1.7 p.
Cycle effective I.3.1 p.
Cycle theoretic fiber I.3.9 p. I.3.10.4 p.
Cycle, algebraic I.3.1 p.
Cycle, degree of a cycle I.3.1.5 p.
Cycle, essentially the same I.3.8 p.
Cycle, nonnegative I.3.1 p.
Cyclic cover II.6.1.5 p.
Deformation, general deformation II.3.6 p.
Degree (of a cycle) I.3.1.5 p.
Degree * uniruling IV.l.l p.
Degree, anticanonical II.3.12 p.
Del Pezzo surface III.3.1 p.
DVR T.5 p.3
E( ),  I.2.2.2—3 p. I.2.5 p. I.2.2.2—3 p. I.2.5 p.
Equivalence (algebraic, effective algebraic, effective rational, numerical, rational) II.4.1—2 pp.
Equivalence relation IV.4.2 p.
Equivalent (algebraically, rationally, numerically) II.4.1—2 pp.
Equivalent, set theoretically equivalent IV.4.2 p.
Essentially independent (family of cycles) I.3.8 p.
Exceptional set VI.1.1 p.
Extremal ray II.4.9 p.
Extremal subcone II.4.9 p.
Extremal, *-negative extremal ray II.4.9.4 p.
Fam( ) II.3.12 p. II.4.1.9 p.
Family of algebraic cycles I.3.10—11 p.
Family of rational curves II.2.11 p.
Family of rational curves through * II.2.11 p.
Family, unsplit family of rational curves IV.2.1 p.
Fano variety V.l.l p.
Fano variety of lines V.4.2 p.
Fano variety,  -fano variety V.l.l p. -fano variety V.l.l p.
FC I.6.3 p.
Fiat section II.5.4 p.
Fiber, cycle theoretic I.3.9 p. I.3.10.4 p.
Fibration, maximal rationally chain connected IV.5.1 p.
Fibration, maximal rationally connected IV.5.3 p.
Fibration, rationally chain connected IV.5.1 p.
Field of condition I.4.7 p.
Field of definition I.1.15 p.
Field, 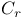 -field IV.6.4.1 p. -field IV.6.4.1 p.
Field, Chow field I.3.24.1 p.
Field, Chow fild condition I.4.7 p.
Finite type (property) II.5.10.2 p.144
Flat pull back I.3.1.4 p.
Form, Cayley I.3.24.1 p.
Form, Chow I.3.24.1 p.
Form, normic IV.6.4.2 p.
Free morphism II.3.1 p.
Free morphism over * II.3.1 p.
Free morphism, minimal IV.2.8 p.
Fundamental cycle I.3.1.3 p.
General deformation II.3.6 p.
General point T.4 p.
General, very general point T.4 p.3
Generically unobstructed I.2.11 p.
| Geometrically irreducible II.2.9.1 p.
Geometrically normal I.6.4.3 p. II.2.9.1 p.
Geometrically rational II.2.1 p. IV.3.1 p.
Geometrically rational components II.2.1 p.
Geometrically reduced I.6.4.3 p.
Geometrically ruled IV.1.1.4 p.
Geometrically smooth I.6.4.3 p.
Grass( , ) I.1.7.1 p. I.1.7.2 p.
Grassmann functor I.1.7.1 p.
Group scheme I.1.10.2 p.
Handle II.7.7 p.
Hilb( ), I.1.3 p.9 I.1.4 p.10 I.5.2 p.74 I.1.3 p.9 I.1.4 p.10 I.5.2 p.74
Hilbert functor I.1.3 p. I.5.2 p.
Hilbert polynomial I.1.2.1 p.
Hom( , ) I.1.9 p. I.1.10 p.
Hom( , , ) II.1.4 p. II.1.4 p.
Horn functor I.1.9 p.
Incidence correspondence I.3.23 p.
Index (of a Fano variety) V.1.9 p.
Inseparably unirational IV.3.12.1 p.
Inseparably uniruled VI.3.12.1 p.
Intersection number VI.2.6 p. VI.2.7.4 p.
Line V.1.13 p.
Locally unobstructed I.2.11 p.
Locus II.2.3 p. III.1.5.1 p.
Locus( ) II.2.3 p. III.1.5.1 p.
MAP T.2 p.
Maximal rationally chain connected fibration IV.5.3 p.
Maximal rationally connected fibration IV.5.1 p.
Minimal (free morphism) IV.2.8 p.
Modification, ruled VI.1.6 p.
Modification, uniruled VI.1.6 p.
Morphism T.2 p.
MRC-fibration IV.5.3 p.
MRCC-fibration IV.5.1 p.
N( ), NE( ), II.4.7 p. II.4.7 p.
Nef vector bundle V.3.9 p.
Nef, *-nef II.4.2.7 p.
Nonnic form IV.6.4.2 p.
Normal form IV.4.4.5 p.
Normal point I.6.4 p.
Normal, geometrically II.2.9.1 p.
Normal, serni I.7.2.1 p.
Normal, weakly I.7.2.1 p.
Numerical equivalence II.4.2 p.
Obs( ) I.2.6 p.
Obstruction I.2.2.3 p. I.2.5 p.
Obstruction space I.2.6 p.
Obtained from * by attaching trees II.7.4 p.
Picard number II.4.6 p.
Point, general T.4 p.
Point, normal I.6.4 p.
Point, reduced I.6.4 p.
Point, smooth I.6.4 p.
Point, very general T.4 p.3
Prerelation IV.4.6 p.
Prime divisor (of a field) VI.1.3.1 p.
Proalgebraic relation IV.4.2 p.
Product (of algebraic relations) IV.4.3 p.
Product (of relations) IV.4.1 p.
Pull-back, Chow pull-back I.3.18 p.
Pull-back, flat I.3.1.4 p.
Push forward I.3.1.2 p. I.6.7 p.
Quot scheme I.5.15 p.
Quot( , ) I.5.15—16 p.
R( , ) III.3.3 p.
rational II.2.1 p. IV.3.1 p.
Rational equivalence II.4.1 p.
Rational, geometrically II.2.1 p.
Rationally chain connected IV.3.2 p.
Rationally chain connected fibration IV.5.1 p.
Rationally connected IV.3.2 p.
Rationally, maximal rationally chain connected fibration IV.5.1 p.
Rationally, maximal rationally connected fibration IV.5.3 p.
Rationally, separably rationally connected IV.3.2 p.199
RatLocus( ) II.2.3 p.
Ray, *-negative extremal II.4.9.4 p.
Ray, extremal II.4.9 p.
Reduced point I.6.4 p.
Reduced, geometrically II.2.9.1 p.
Reduction, mod *-reduction II.5.10.1 p.
Relation IV.4.1 p.
Relation algebraic IV.4.2 p.
Relation class IV.4.2 p. IV.4.6 p.
Relation, equivalence IV.4.2 p.
Relation, irreducible IV.4.2 p.
Relation, open IV.4.2 p.
Relation, proalgebraic IV.4.2 p.
Relation, proper IV.4.2 p.
Represent (a functor) I.1.1 p.
Root, 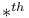 root of * II.6.1.5 p. root of * II.6.1.5 p.
Ruled IV.1.1 p.
Semi normal I.7.2.1 p.
Semi normalization I.7.2.1 p.
Semi positive (vector bundle) II.3.8 p.
Separably rationally connected IV.3.2 p.
Separably ruled IV.1.1 p.
Separably uniruled IV.1.1 p.
Seshadri constant VI.2.18.6 p.
Smooth point I.6.4 p.
Smoothable II.1.10 p. II.7.1 p.
Smoothable fixing * II.7.2 p.
Smoothing II.1.10 p. II.7.1 p.
Smoothing, nearby smoothing II.7.1 p.
Subcomb II.7.7 p.
Supporting function II.4.9 p.
Surface, Del Pezzo surface III.3.1 p.
Tooth II.7.7 p.
TREE II.7.4 p.
u( ),  IV.1.7.3 p.186 IV.1.7.3 p.186
Unirationa, separably IV.3.1 p.
Unirational IV.3.1 p.
Unirational, inseparably IV.3.12.3 p.
Uniruled IV.l.l p.
Uniruled inseparably IV.3.12 p.
Uniruled separably IV.l.l p.
Uniruled with curves of *-degree * IV.1.4 p.
Uniruling, degree * uniruling IV.l.l p.
Univ( ),  I.1.4 p. I.3.21 p. I.1.4 p. I.3.21 p.
Universal element I.1.1 p.
Universal family I.1.1 p.9
Unobstructed I.2.6 p.
Unobstructed generically I.2.11 p.33
Unobstructed locally I.2.11 p.33
Unsplit (family of morphisms or rational curves ) IV.2.1 p.
Unsplit, generically unsplit IV.2.1 p.
Very general point T.4 p.
WDiv( ) II.4.2 p.
Weak normalization I.7.2.1 p.
Weakly normal I.7.2.1 p.
Weighted projective space V.1.3 p.
Well defined family of algebraic cycles I.3.10 p. I.3.11 p.
Well formed (weighted projective space) V.1.3 p.
[] I.3.1.3 p.
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте





 ,
, 
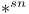 ,
,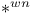
![$*^{[-1]}$](/math_tex/3047feed19ce5b6ff6a3160ebbd5733882.gif)
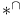

 ,
, 
 ,
,
 ,
, 
 ( )
( )  ,
,
 ,
, 
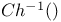












 ,
, 
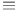

 ,
, 
 ,
, 
 ,
,  ,
, 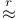
 ,
, 



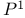 -bungle
-bungle 

 -fano variety
-fano variety 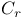 -field
-field 

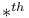 root of *
root of * 
