|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Johnstone P. — Stone Spaces |
|
|
 |
| Предметный указатель |
Absorptive law I 1.4 3
Adjunction I 3.4 17
Adjunction monadic a. I 3.6 21
Alexandrov algebra IV 2.9 140
Alexandrov topology II 1.8 45
Algebraic category I 3.8 23
Algebraic lattice VI 3.6 252
Algebraic poset VII 2.3 288
atom II 1.5 42
Boolean algebra I 1.6 4
Boolean algebra, complete B. a. I 4.4 27
Boolean ring I 1.9 6
Bundle V 1.2 770
Bundle, trivial b. V 1.3 770
C*-algebra IV 4.4 155
C-ideal 112 11
Cartesian category I 3.5 20
Cartesian formula V 1.12 180
Cartesian functor VI 1.3 227
Category I 3.1 15
Category, algebraic c I 3.8 23
Category, cartesian c I 3.5 20
Category, complete c I 3.5 20
Category, concrete c I 3.2 16
Category, equationally presentable c I 3.8 23
Category, filtered c I 3.9 24
Category, finitary algebraic c I 3.7 22
Category, locally small c I 3.2 16
Category, small c I 3.5 19
Cocompletion VI 1.8 231
Coherent axiom V 1.10 178
Coherent formula V 1.10 177
Coherent locale II 3.2 63
Coherent map of locales II 3.3 64
Coherent space II 3.4 65
Colimit I 3.5 19
Colimit, filtered c I 3.9 24
Complement I 1.6 4
Completely regular filter IV 2.3 134
Completely regular ideal IV 2.2 131
Completely regular locale IV 1.5 127
Congruence VI 2.6 240
Continuous lattice VII 2.2 288
Continuous poset VII 2.2 288
Continuous semilattice VII 2.11 296
Continuous semilattice, stably c VII 2.12 296
Coseparator VI 4.1 254
Coverage II 2.11 57
Cozero element IV 2.9 140
Cozero-set IV 2.5 137
Cut III 3.11 109
Display space V 1.4 172
Distributive law I 1.5 3
Distributive law, complete d.1. VII 1.10 278
Distributive law, continuous d 1. VII
Distributive law, infinite d.1. II 1.1 39
F-ring V 4.6 212
F-ring, L-local F-r. V 4.9 216
F-ring, L-simple F-r. V 4.10 216
Field V 1.10 178
Field, formally real f. V 4.11 217
Field, real-closed f. V 4.11 217
Filter (in a lattice or semilattice) I 2.2 12
Filter (in a lattice or semilattice), completely prime f. II 1.3 41
Filter (in a lattice or semilattice), completely regular f. IV 2.3 134
Filter (in a lattice or semilattice), prime f. I 2.2 12
Filter (in a poset) VII 2.5 290
Filter (in a poset), Scott-open f VII 2.5 290
Filter (in a ring), concave prime f. V 4.2 207
Filter (in a ring), prime f V 3.2 192
Filter (in a ring), strictly positive f. V 4.11 218
Filter (on a set) III 2.2 94
Filter (on a set), neighbourhood f. III 2.2 94
Finite (element in lattice) II 3.1 63
Formula, cartesian f. V 1.12 179
Formula, coherent f. V 1.10/77
Formula, regular f. V 1.13 180
Frame II 1.1 39
functor 13 175
Functor, adjoint f. I 3.4 17
Functor, cartesian f. VI 1.3 227
Functor, comparison f. I 3.6 21
Functor, direct image f. V 1.8 175
Functor, faithful f. I 3.4 18
Functor, final f. VI 1.5 227
Functor, finitary f. I 3.9 24
Functor, full f. I 3.4 18
Functor, inverse image f. V 1.8 J 75
Functor, monadic f. I 3.6 21
Heyting algebra I 1.10 8
Ideal (in a lattice or semilattice) I 2.1 11
Ideal (in a lattice or semilattice), C-i. 112 11
Ideal (in a lattice or semilattice), completely regular i. IV 2.2 131
Ideal (in a lattice or semilattice), fixed (maximal) i. IV 3.5 145
Ideal (in a lattice or semilattice), maximal i. I 2.4 13
Ideal (in a lattice or semilattice), prime L I 2.2 12
Ideal (in a lattice or semilattice), principal L I 2.1 //
Ideal (in a lattice or semilattice), regular i. IV 2.2 133
Ideal (in a poset) VII 2.1 286
Ideal (in a ring), L-l V 4.6 211
Ideal (in a ring), neat i. V 2.8 188
Ideal (in a ring), radical i. V 3.2 193
ind-object VI 1.2 225
Integral domain V 3.11 203
Irreducible (closed set) II 1.6 43
Irreducible (L-ideal) V 4.6 212
Join I 1.2 7
Join, directed j. I 4.1 25
Join-semilattice 11 32
Jonsson — Tarski algebra VI 2.5 238
L-ideal V 4.6 211
L-ideal, irreducible L-i. V 4.6 212
L-ring V 4.4 210
Lattice I 1.4 2
Lattice, algebraic 1. VI 3.6 252
Lattice, complete 1. I 4.3 27
Lattice, completely distributive l. VII 1.10 278
Lattice, continuous l. VII 2.2 288
Lattice, distributive l. I 1.5 5
Lattice, normal (distributive) 1. 11 3.6 67
Lawson map VII 2.10 295
Lawson topology VII 3.3 301
Limit (of a diagram) I 3.5 19
Limit (of a filter) III 2.2 94
Local homeomorphism V 1.5 172
Local homomorphism (of rings) V 3.5 196
Local ring V 2.7 186
Locale II 1.1 39
Locale, 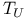 1. III 1.5 84 1. III 1.5 84
Locale, coherent 1. II 3.2 63
Locale, compact 1. III 1.1 80
Locale, completely regular 1. IV 1.5 127
Locale, exponentiable 1. VII 4.10 317
Locale, extremally disconnected 1. III 3.5 102
Locale, injective 1. VII 4.9 316
Locale, locally compact 1. VII 4.2 310
Locale, normal 1. IV 1.6 128
Locale, regular 1. III 1.1 81
Locale, spatiall. II 1.5 43
Locale, stably locally compact 1. VII 4.6 313
| Locale, strongly Hausdorff l. II 13 82
Locale, Vietoris l. III 4.3 113
Locale, zero-dimensional 1. III 1.1 81
Lower set I 2.1 11
MacNeille completion III 3.11 109
Meet I 1.4 2
MI-space IV 4.12 163
Natural transformation I 3.1 16
Nilradical V 3.6 197
Normal (distributive lattice) II 3.6 67
Normal (locale) IV 1.6 128
Nucleus II 2.2 48
Nucleus, closed n. II 2.4 50
Nucleus, dense n. II 2.4 50
Nucleus, double-negation n. II 2.4 51
Nucleus, open n. II 2.4 50
Object I 3.1 15
Object, E-projective o. III 3.1 98
Object, exponentiable o. VII 4.10 317
Object, finitely-presentable o. VI 1.8 231
Object, projective o. III 3.1 98
Order-Hausdorff VII 1.1 271
Order-normal VII 1.2 271
Pierce representation V 2.3 183
Point (of a locale) II 1.3 41
POSET I 1.1 1
Poset, algebraic p. VII 2.3 288
Poset, continuous p. VII 2.2 288
Poset, Dedekind-complete p. IV 4.11 161
Poset, directed p. I 4.1 25
Poset, topological p. VII 1.1 270
Positive cone V 4.1 206
Presheaf V 1.3 171
Prime element 11 1.3 41
Prime filter (in a lattice) I 2.2 12
Prime filter (in a ring) V 3.2 192
Prime ideal (in a lattice) I 2.2 12
Pro-object VI 1.9 233
Profinite VI 2.3 236
Proper map III 3.8 104
Pseudoiattice IV 3.2 143
Reaicompact space IV 3.7 147
Reaicompactification IV 3.8 148
Real point (of  X) IV 3.7 147 X) IV 3.7 147
Real point (of spec A) V 4.11 217
Really inside IV 1.4 126
Reflection I 3.4 18
Regular axiom V 1.13 180
Regular element (in a Heyting algebra) I 1.13 10
Regular formula V 1.13 180
Regular ideal IV 2.2 133
Regular locale III 1.1 81
Regular monomorphism 1 3.5 20
Regular ring V 2.6 185
Ring, domain representable r. V 3.11 204
Ring, exchange r. V 2.7 187
Ring, F-r V 4.6 212
Ring, formally real local r. V 4.13 219
Ring, Gelfand r. V 3.7 199
Ring, indecomposable r. V 2.2 182
Ring, L-r V 4.4 210
Ring, local ordered r. V 4.3 208
Ring, local r. V 2.7 186
Ring, ordered local r. V 4.13 220
Ring, ordered r. V 4.1 206
Ring, regular r. V 2.6 185
Ring, semiprime r. V 3.2 193
SCALE IV 1.4 726
Semilattice I 1.3 2
Semilattice, complete s. I 4.3 26
Semilattice, continuous s. VII 2.11 296
Semilattice, join-s. I 1.3 2
Semilattice, Lawson s VII 3.3 301
Shadow V 4.3 208
Sheaf V 1.3 171
Sheaf, Pierce s. V 2.3 183
Sheaf, Zariski s. V 3.3 194
Site 112 11
Sober space II 1.6 43
Soberification II 1.7 44
Space, 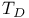 -s. II 1.7 44 -s. II 1.7 44
Space, coherent s. II 3.4 65
Space, display s. V 1.4 772
Space, exponentiable s. VII 4.12 320
Space, extremally disconnected s. II 3.5 102
Space, injective s. VII 4.7 314
Space, locally compact s. II 2.13 61
Space, ordered s VII 1.1 270
Space, projective s. III 3.7 103
Space, pseudocompact s. IV 3.7 148
Space, reaicompact s. IV 3.7 147
Space, Sierpinski s. VI 4.6 260
Space, Sober s. II 1.6 43
Space, Stone s. II 4.2 70
Space, totally disconnected s. II 4.1 69
Space, totally order-separated s II 4.7 74
Space, totally separated s. II 4.1 69
Space, Vietoris s. III 4.1 111
Space, zero-dimensional s. II 4.1 69
Specialization II 1.8 45
Spectrum II 3.4 66
Spectrum, Brumfiel s. V 4.2 208
Spectrum, domain s. V 3.11 203
Spectrum, field s. V 3.12 205
Spectrum, Keimel s. V 4.6 212
Spectrum, maximal s. II 3.5 66
Spectrum, Pierce s. V 2.3 183
Spectrum, real s. V 4.11 218
Spectrum, Zariski s. V 3.1 192
Stably continuous VII 2.12 296
Stably locally compact VII 4.6 313
Stone space II 4.2 70
Stone space, ordered S. s. II 4.7 74
Stone — Cech compactification IV 2.1 130
Subframe II 1.1 40
Sublocale II 2.3 50
Sublocale, closed s II 2.4 50
Sublocale, dense s. II 2.4 50
Sublocale, flat s. III 1.11 90
Sublocale, open s II 2.4 50
Symmetric difference I 1.8 5
Topology, Alexandrov t. II 1.8 45
Topology, interval t. VII 1.11 279
Topology, Lawson t. VII 3.3 301
Topology, lower interval t. III 4.2 113
Topology, patch t. II 4.5 72
Topology, Scott t. II 1.9 46
Topology, Sierpinski t. VI 4.6 260
Topology, upper interval t II 1.8 45
Topology, Vietoris t. Ill 4.2 112
Topology, Zariski t. IV 3.3 145 V
Ultrafilter III 2.1 93
Upper set II 1.8 45
Vietoris locale III 4.3 113
Vietoris space III 4.1 111
Wallman base IV 2.4 135
Wallman compactification IV 2.4 136
Way below VII 2.2 287
Well inside III 1.1 80
Zariski representation V 3.5 195
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



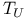 1.
1.  X)
X) 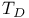 -s.
-s.