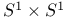|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Weeks J.R. Ч The shape of space |
|
|
 |
| ѕредметный указатель |
# symbol 75
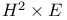 geometry 244Ч247 250Ч251 geometry 244Ч247 250Ч251
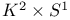 58Ч59 248 58Ч59 248
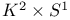 as a bundle 232 as a bundle 232
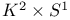 , as a product 91 , as a product 91
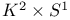 , circles in the sky of 306 , circles in the sky of 306
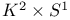 , surfaces in 128 , surfaces in 128
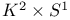 , view in 104Ч107 , view in 104Ч107
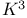 237 250 237 250
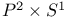 96 250 96 250
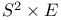 geometry 243Ч245 250 geometry 243Ч245 250
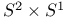 91Ч97 250 91Ч97 250
1/2 turn manifold 108 249
1/3 turn manifold 123 231 249
1/4 turn manifold 107Ч109 229Ч233 249
1/6 turn manifold 123 231 249
3/4 turn manifold 108
Abbreviations for manifolds 73Ч75
Admit a geometry 164
Aliens, extracosmic 215
Ancient Greeks 279
Angle-sum of hyperbolic triangle 154Ч156
Angle-sum of spherical triangle 136Ч144
Antipodal triangle 140
Area of hyperbolic triangle 154Ч156
Area of spherical triangle 136Ч144
Aristotle 279
Astria 4
Ball 200Ч201
big bang 259Ч260 262Ч263 265Ч267 295Ч296
Big bang, correct picture 267
Big bang, incorrect picture 266
Big bang, philosophical aspects 273Ч278
Biplanes 13Ч14 99Ч103 113Ч114
Blackbody spectrum 298Ч299
Bundle 229Ч242 251Ч255
CAP 365
Cell-division 166Ч169
Chess on a Klein bottle 50 53Ч55
Chess on a torus 17Ч20
China 279
Circles in the sky 295Ч308
Classes of geometries 246Ч248
Closed manifold 42Ч44
CMB see "Cosmic microwave background"
COBE see "Cosmic background explorer"
Cone point 118Ч122 157Ч159
Connected sum 65Ч81
Connected sum, definition 70
Conway 362
Cornish 306
Cosmic background explorer 298Ч299
Cosmic crystallography 285Ч293
Cosmic microwave background 297Ч302 307
Cross surface 374Ч375
Cross surface, double 375
Cross surface, triple 375
Crosscap 365Ч366
Crosshandle 364
Crosshandle in presence of crosscap 372Ч373
Crosshandle, homeomorphic to two crosscaps 370Ч372
Curvature 149Ч151 175Ч184
Curvature, Gaussian 181
Curvature, measurement of 37 182 208Ч210 269Ч271
Curvature, sectional 244Ч247
Cusp 43Ч44
Cylinder 83Ч84
de Sitter 282
Democritus 279
Dodecahedral spaces 219Ч224
Double cross surface 375
Double disk method 201Ч205
Double lune 139Ч141
Double torus 374
Doughnut surface 9 30
Doughnut surface with cusp 43Ч44
Dyck's surface 375
Dyck's Theorem 372Ч373
Einstein 261Ч262 281Ч282
Elliptic geometry 135Ч147 199Ч212
Elliptic geometry for Poincare dodecahedral space 220Ч224
Elliptic geometry on a surface 157Ч158 162Ч164
Elliptic geometry, definition 149Ч150
Elliptic geometry, sample three-manifolds 248
Euclidean geometry, definition 149Ч150
Euclidean geometry, list of three-manifolds 248Ч249
Euler number 165Ч185 374
Euler number, definition 174
Euler number, general description 165
Expansion of the universe 260Ч263 265Ч269
Extrinsic property 31Ч35
Flat geometry 120Ч122
Flat surfaces and three-manifolds 99Ч124 273
Flat torus 13Ч20 23Ч24
Flatland 3Ч4 187S
Flatland story, beginning 3Ч9
Flatland story, continuation 45Ч47
Flatland story, ending 65Ч69
Four dimensions 187Ч197
Friedmann 261Ч262 282
Galaxies 260Ч261 289
Galaxies, catalogs of 292Ч293
Gauss 37 208Ч210
Gauss Ч Bonnet formula 165Ч184
Gauss Ч Bonnet formula for elliptic geometry 174
Gauss Ч Bonnet formula for Euclidean geometry 175
Gauss Ч Bonnet formula for hyperbolic geometry 174
Gauss Ч Bonnet formula for surfaces of constant curvature 181
Gauss Ч Bonnet formula for surfaces of varying curvature 182Ч184
Gaussian curvature 181
Geocentric universe 279Ч280
Geodesic 37 136
Geometry 26Ч29
Geometry, Relativity and the Fourth Dimension 190Ч192 195Ч197
Girard 137
Global geometry 41
Global property 39Ч41
Global topology 40Ч41
Gluing 13
God 275
Great circle 136Ч137
Great two-sphere 203 207
Half turn manifold 108 249
Half turn manifold, surfaces in 128
Handle 363
Handle in presence of crosscap 372Ч373
Hexagonal three-torus 122Ч123
Hexagonal torus 111Ч120
Hinton 4
Homeomorphic surfaces 362
Homogeneity 41Ч42
Homogeneity of the Universe 263Ч264
Homogeneous geometry 41Ч42 149Ч150
Homogeneous geometry on surfaces 157Ч164
Homogeneous geometry on three-manifolds 219Ч228 243Ч255
Homogeneous three-manifold 96
Hubble 262
Hubble, constant 262 264
Hyperbolic 3-manifolds 219Ч221 249Ч250 273
Hyperbolic 3-manifolds, cosmic crystallography in 291
Hyperbolic geometry 149Ч156 213Ч218
Hyperbolic geometry for "typical" three-manifolds 249Ч250
Hyperbolic geometry for Seifert Ч Weber space 219Ч221
Hyperbolic geometry for surfaces 157Ч164
Hyperbolic geometry, definition 149Ч151
Hyperbolic geometry, Thurston's work 249Ч250 255
Hyperbolic n-gon 170
Hyperbolic paper 151Ч154
Hyperbolic plane 149Ч156
Hyperbolic space 213Ч218 282
| Hyperbolic triangle 154Ч156 214Ч216
Hypersphere 201Ч210
Intrinsic point of view 38Ч39
Intrinsic property 31Ч39
Isotropic geometry 244Ч246
Isotropic three-manifold 96
Isotropy of the microwave background 299Ч300
Isotropy of the Universe 263Ч265
Jungle gym in a nonorientable three-manifold 58Ч59
Jungle gym in a three-torus 21Ч22
Jungle gym, twisted Euclidean 251Ч253
Klein 280
Klein bottle 48Ч58
Klein bottle in four-dimensional space 191
Klein bottle, chess on 50 53Ч55
Klein bottle, cosmic crystallography in 290Ч292
Klein bottle, cut into two pieces 74
Klein bottle, limerick 73
Klein bottle, solid 236
Klein bottle, three-dimensional analog of 237
Klein bottle, tic-tac-toe on 50Ч54
Klein perforation 371
Knotted sphere 193Ч195
Lachieze-Rey 287
Last scattering surface 301Ч308
Lehoucq 287
Lemaitre 262
Leucippus 279
Light-year 260
Local geometry 40Ч41
Local property 39Ч41
Luminet 287
Lune, double 139Ч141
Manifold 11
Manifold, precise definition 40Ч41
Manifold-with-boundary 42
MAP see "Microwave anisotropy probe"
Microwave anisotropy probe 307Ч308
Microwave background radiation 297Ч302 307
Milky Way 260
Mirror reversal 45Ч49
Mirror reversal and orientability 58
Moebius bridge 371
Moebius strip 47Ч49 125Ч126
Moebius strip, two-sided 129
Multiconnected space 280
n-gon 169Ч170
Negative curvature 151
Nonhomogeneous 41
Nonorientable manifold 58
Octahedral space 227
One-dimensional manifold 41
One-sided surface 125Ч131
One-sided surface, definition of 125
Open manifold 42Ч44
Ordinary surface 368
Orientable manifold 58
Orientation-reversing path 58
Pair separation histogram 290Ч291
Patchwork quilt 368
Penzias 297
Perforation 367
Planck satellite 307Ч308
plasma 295Ч297
Poincare conjecture 280
Poincare dodecahedral space 220Ч224 248
Poincare dodecahedral space, circles in the sky of 306
Positive curvature 149
PRODUCT 83Ч97
Product, geometrical 86Ч88 91
Product, multiplication 86
Product, three-dimensional 89Ч97
Projective plane 59Ч64
Projective plane, minus a disk 70Ч73
Projective plane, nomenclature 374
Projective three-space 62Ч64 210Ч212 248 282
Puncto 135
Quarter turn manifold 107Ч110 229Ч233 249
Quarter turn manifold, circles in the sky of 306
Quarter turn manifold, cosmic crystallography in 291
Quaternionic manifold 226Ч227
RADIANS 136
Riemann 280
Rubber band with twist 31Ч33
Schwarzschild 280
Sectional curvature 244Ч247
Seifert Ч Weber space 219Ч221 224 249
Seifert Ч Weber space, circles in the sky of 306
Sheep 86
Solid 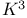 237 237
Solid 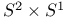 237 237
Solid doughnut 236
Solid Klein bottle 236
Solve geometry 254Ч255
Spacetime 195Ч197 272Ч278
Spergel 306
Sphere 135Ч147 199Ч200
Sphere vs. ball 200Ч201
Sphere, knotted 193Ч195
Sphereland 135Ч136
Spherical 3-manifolds 219Ч224 273
Spherical 3-manifolds, cosmic crystallography in 292
Spherical n-gon 169Ч170
Spherical triangle 136
Spherical triangle, area and angles 136Ч144
Spirits 190Ч193
Starkman 306
Superclusters 289Ч293
Surfaces 11
Surfaces, classification of 361Ч375
Surfaces, Classification Theorem 368
Surfaces, nonredundant list of 80
Surfaces, ordinary 368
Surfaces, redundant list of 76
Surfaces, triangulated 367
Telescope 280
Tetrahedral space 226Ч227
Three-manifold, formal definition 40
Three-manifold, informal definition 11
Three-sphere 199Ч210 248 280 282
Three-torus 20Ч24 249
Three-torus as a product 89Ч91
Three-torus, circles in the sky of 302Ч306
Three-torus, how corners fit 224Ч225
Three-torus, introduced to astronomers 280Ч281
Three-torus, oblong 41
Three-torus, view in 103Ч105
Thurston 249 255
Tic-tac-toe on a Klein bottle 50Ч54
Tic-tac-toe on a torus 14Ч17 103
topology 26Ч31
Torus, 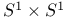 84Ч85 87 84Ч85 87
Torus, chess on 17Ч20
Torus, double 374
Torus, drawn as a doughnut surface 9 30
Torus, flat 13Ч20 23Ч24
Torus, flat torus vs. doughnut surface 30Ч31 41
Torus, hexagonal 111Ч120
Torus, three-dimensional see "Threetorus"
Torus, tic-tac-toe on 14Ч17 103
Torus, triple 374
Torus, twisted 239Ч241 252Ч253
Triangle, Euclidean 144
Triangle, hyperbolic 154Ч156 214Ч216
Triangle, spherical 136Ч144
Triangulated surface 367
Triple cross surface 375
Triple torus 374
Twisted 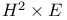 geometry 254 geometry 254
Twisted 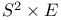 geometry 254 geometry 254
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



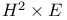 geometry
geometry 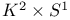
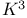
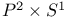
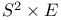 geometry
geometry