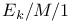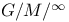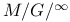|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Karlin S., Taylor H.E. Ч A Second Course in Stochastic Processes |
|
|
 |
| ѕредметный указатель |
Absorbing barrier 16Ч18 19
Absorbing boundary 251
Absorbing state 24 29 155
Additive functional 254Ч255 308Ч313
Arcsine law 224Ч226 473
Attainable boundary 230
Attracting boundary 228 249
Backward equation for Brownian motion 217
Backward equation for for diffusion processes 214Ч216
Backward equation for for Kac functional 222Ч224
Backward equation for for Markov chain 143Ч144
Ballot problem 107 134Ч136
Bessel process 175Ч176 327 336
Bessel process, boundary behavior 238Ч239
Bessel process, spectral representation 338
Birth and death process 142
Boundary behavior, and infinitesimal operator 305Ч307
Boundary classifications 234 250
Boundary criteria 232Ч234
Branching process 383 384
Brownian bridge 268 269
Brownian motion 169Ч170 211 323 377 379 385 386 388 389 394
Brownian motion, absorbed 170 392
Brownian motion, and white noise 343
Brownian motion, arcsine law 224Ч226
Brownian motion, backward equation 217
Brownian motion, boundary behavior 228Ч229 230 236
Brownian motion, compounded 378
Brownian motion, conditioned process 267Ч272 388
Brownian motion, control problem 212
Brownian motion, geometric 175 359Ч360 380
Brownian motion, infinitesimal operator 289 297
Brownian motion, instantaneous return process 261
Brownian motion, n-dimensional 291Ч292 299 312Ч313 380 382 393
Brownian motion, radial process 335Ч336
Brownian motion, reflected 170 327 337 379 392
Brownian motion, resolvent 288
Brownian motion, spectral representation 337 393
Brownian motion, standard 197 205
Brownian motion, with drift 205
Busy period 513Ч519
Cash inventory model 211Ч212
Chapman Ч Kolmogorov equation 286
Compound Poisson process 426Ч440
Compound Poisson process, decomposition of 433Ч436
Compound Poisson process, sum of 430Ч431
Conditional diffusion process 261Ч272 387
Conditional diffusion process, boundary behavior 263Ч264
Conditional diffusion process, Green function 264Ч265
Conservative diffusion 161
Conservative process 143
Convergence to diffusions 168
Coupling 93
Differential operator 388
Diffusion coefficient 159
Drift coefficient 159
Dynamical systems 343Ч345
Dynkin condition 163 165
Dynkin formula 297Ч299 308Ч313
Dynkin formula, applications 299
Ehrenfest urn model 171
Elastic boundary 255Ч257
Empirical distribution 113Ч116 119Ч123
Entrance boundary 235 246 382
Entrance boundary, stationary distribution 241Ч242
Excessive function see УSuperregular sequenceФ
Exchangeable random variables 454 516
Exit boundary 233Ч234 246
Exit time 302Ч303
Feller property 291
Forward equation for diffusion processes 219
Forward equation for Markov chain 143 144
Fundamental matrix 24
Gene frequency model 177 206Ч208 361Ч362 381 387 390
Gene frequency model, boundary behavior 239Ч241
Gene frequency model, spectral representation 336Ч337
Gene frequency model, with mutation 177Ч179 180Ч183 208Ч211 239Ч241 265Ч266
Gene frequency model, with mutation and selection 222
Gene frequency model, with selection 180 184Ч188
Genetic recombination 272Ч284
Green function 198Ч202 287
Green function, and resolvent operator 293
Green function, for Brownian motion 205
Harmonic function see УRegular sequenceФ
Hewitt Ч Savage 0Ч1 law 477
Hille Ч Yosida theorem 296
Hitting time 158 162 192 226
Hitting time of boundary 228 242Ч243
Infinitesimal generator 286
Infinitesimal matrix 145
Infinitesimal mean 159
Infinitesimal operator 195 287 294Ч295
Infinitesimal operator, and boundary behavior 305Ч307
Infinitesimal operator, as differential operator 303Ч305
Infinitesimal operator, domain of 307Ч308
Infinitesimal operator, Dynkin form 300Ч302
Infinitesimal parameters 159
Infinitesimal variance 159
Input distribution 489
Instantaneous return process 260Ч261
Instantaneous state 147
Interchangeable 108Ч113
Ito integral 346Ч347 356Ч357
Ito transformation formula 173 347Ч348 371Ч372 389
Ito transformation formula, applications 374Ч375
Jacobi diffusion 335
Jump boundary 258Ч260
Kac functional 222Ч224 313Ч316 393
Killing rate 204 313Ч316
Killing time 161 382
Killing time, example 272Ч284
Kolmogorov condition 465
Ladder index 95
Ladder random variable 464Ч465 480
Levy process 319 432Ч433
Lightning model 446
Local time 198 207 251Ч253 316Ч324
Local time, inverse of 317Ч318
Logistic equation 360Ч361
Markov time 149Ч150
Martingale 167 308Ч312 325Ч327 371 376Ч377 382
Martingale and stochastic integrals 352Ч355
| Maximum random variable 451 463 483Ч484 486
Minimal process 148
Multiplicative functional 313Ч316
Mutation see also УGene frequency modelФ
Mutation in population 188Ч191
Natural boundary 235Ч236 246
Natural scale 196
Occupation time 252 452
Optimal allocation model 367Ч368
Optimal growth model 366Ч367
Optimal stopping 50Ч64 68Ч69
Option price model 365Ч366 389
Order statistics 100Ч107 124 125 129
Ornstein Ч Uhlenbeck process 170Ч173 183 345Ч346 379 380
Ornstein Ч Uhlenbeck process, backward equation 218
Ornstein Ч Uhlenbeck process, boundary behavior 237
Ornstein Ч Uhlenbeck process, in n dimensions 292
Ornstein Ч Uhlenbeck process, radial process 333Ч334
Ornstein Ч Uhlenbeck process, spectral representation 332Ч333
Ornstein Ч Uhlenbeck process, stationary distribution 221
Periodic class 6Ч10 78
Poisson point process see also УPoisson processФ
Poisson point process, spatial 436Ч440
Poisson process and uniform distribution 403 404
Poisson process in astronomy 404Ч405
Poisson process, spatial 398Ч403 441 443 445
Population growth model 188Ч191 354Ч355 358 378 382 383 390
Population growth model, boundary behavior 239
Population growth model, geometric 413Ч416
Population growth model, in space and time 416Ч419
Population growth model, spectral representation 334
Population growth model, two types 444
Population growth model, with age structure 419Ч426
Population growth model, with immigration 405Ч408
Population growth model, with mutation 408Ч413
Production and consumption model 363Ч365
Progressively measurable 369
Quasi-left continuity 163
Queue discipline 489
Queueing process 394
Queueing process, 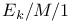 506Ч510 506Ч510
Queueing process, 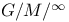 522 522
Queueing process, 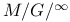 449 521 522 449 521 522
Queueing process,  519Ч520 519Ч520
Queueing process, embedded Markov chain 497Ч503
Queueing process, G/M/1 504Ч506
Queueing process, GI/G/1 524
Queueing process, GI/GI/1 492Ч496
Queueing process, GI/M/s 511Ч513
Queueing process, M/G/1 523
Queueing process, M/GI/1 497Ч503
Queueing process, M/M/l 490Ч492 519 520 524
Queueing process, M/M/s 519
Queueing process, notation 490
Queueing process, with balking 520Ч521
Quiz show 56Ч58
Radial Brownian motion see УBessel processФ
Random time change 253Ч255
Random walk 25 26 67 82 97 98 99
Random walk, optimal stopping 58Ч59
Random walk, spectral representation for 10Ч23
Recurrence 72Ч76 83 153 155
Recurrence, criterion for 73
Recurrent class 9 23 35
Recurrent Markov chain 3Ч4 65 66
Recurrent Markov chain, criterion for 37Ч40 47 49
Recurrent state 34
Reflecting barrier 14Ч16
Reflecting boundary 251
Regular boundary 232Ч233
Regular diffusion 158
Regular sequence 44Ч45 83
Renewal Theorem 93Ч95
Renewal theory 482
Resolvent operator 287 292Ч294
Reversed process 42 69
Scale function 194 226
Scale measure 227
Semigroup theory 305
Semigroup theory for Markov processes 285Ч294
Service distribution 489
Shock model 429Ч430
Signal detection model 368
Spectral representation, for absorbed Brownian motion 393
Spectral representation, Jacobi diffusion 335
Spectral representation, Markov chain 5 23
Spectral representation, matrix 1Ч3
Spectral representation, Ornstein Ч Uhlenbeck process 332Ч333
Spectral representation, population growth model 334
Spectral representation, random walk 14Ч18
Speed density 195 197
Speed measure 195 227
SpitzerТs identity 460 472
Stable state 146
Standard process 162
Standard transition function 138
Stationary distribution 220Ч221 236 241Ч242 386
Stationary distribution, generalized 37 42Ч43
Sticky boundary 257Ч258
Stochastic differential equation, solution of 373Ч374
Stopping rule problems see УOptimal stoppingФ
Stratonovich integral 346Ч347 351 353Ч354 356Ч358 390Ч391
Strength model 439Ч440
Strong Markov property 149Ч152
Subadditive function 139
Subregular sequence 44Ч45
Superregular functions, transient Markov chains 47
Superregular majorant 56 59Ч62
Superregular sequence 44Ч45 52Ч53 66
Taboo probabilities 31Ч32
Total positivity 167
Transience 75
Transient class 24
Transient Markov chain 67
Trap state 378
Unattainable boundary 230
Virtual waiting time 513Ч519
Warrant price model see УOption price modelФ
White noise 342Ч343
Wong Ч Zakai integral 348Ч351
Wright Ч Fisher model see УGene frequency modelФ
wronskian 200
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте