|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Gardiner C.W.W., Haken H. Ч Handbook of Stochastic Methods: For Physics, Chemistry and the Natural Sciences |
|
|
 |
| ѕредметный указатель |
Absorbing boundary condition for backward FPE 129
Additive invariants 336
Adiabatic elimination in quantum systems 391
Adiabatic elimination in quantum systems of fast variables 195Ч234
Adiabatic elimination in quantum systems of inhomogeneous modes in reaction diffusion systems 328Ч331
Almost certain 29
Arrhenius formula 141
Autocorrelation function 16 58
Autocorrelation function and Poisson rep. 289Ч294
Autocorrelation function for Markov process 64Ч66
Autocorrelation function in terms of eigenfunctions 131
Autocorrelation function with detailed balance 149
Autocorrelation matrix and eigenfunctions 168
Autocorrelation matrix, stationary 65
Backward differential Chapman Ч Kolmogorov equation 55
Backward FPE, boundary conditions for 128
Backward master equation and first passage times 259
Baker Ч Hausdorff formula 387
Bargmann states, defined 377
Bath correlation functions 389
Bernoulli distribution 72
Bernoulli trials 42
Birth-death master equation 10 13
Birth-death master equation and bistability 354 357
Birth-death master equation in quantum harmonic oscillator 395
Birth-death master equation, one-variable 236 262
Birth-death process 8
Birth-death process for flow 332Ч336
Birth-death processes, boundary, conditions for 257 259
Birth-death systems, many-variable 262 277
Bistability 342
Bistability in multivariable systems 357 371
Bistability with birth-death master equation 354Ч357
Bistable system, chemical 241 245
Boltzmann equation from Boltzmann master equation 337
Boltzmann master equation 303 336Ч339
Boltzmann master equation in Poisson representation 338 341
Boundary conditions for backward FPE 128
Boundary conditions for birth-death processes 257 259
Boundary conditions for FPE 118Ч125
Boundary conditions for FPE at a discontinuity 121
Boundary conditions for FPE at infinity 123
Boundary conditions for FPE, absorbing 121
Boundary conditions for FPE, reflecting 121
Boundary conditions for KramersТ equation 205
Boundary conditions for many-variable FPE 146
Boundary conditions for Smoluchowski equation 205
Brownian motion 2
Brownian motion and adiabatic elimination 195
Brownian motion in double potential 365Ч371
Brownian motion, continuous sample path 46
Brownian motion, corrections to Smoluchowski equation 206Ч210
Brownian motion, KramersТ equation for 155
Brownian particle 6
Cauchy process 46Ч47
Central limit theorem 37
Chaos 1
Chapman Ч Kolmogorov equation 5 43Ч44
Chapman Ч Kolmogorov equation, differential 47Ч51
Characteristic function 32
Characteristic function of a Gaussian 36
Characteristic function, quantum 386Ч388
Chemical FPE 266
Chemical intermediates, elimination of 218
Chemical reaction 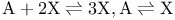 300Ч301 300Ч301
Chemical reaction 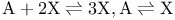 , master equation 241 , master equation 241
Chemical reaction 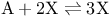 , in Poisson rep. 294 , in Poisson rep. 294
Chemical reaction 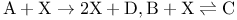 , solution of ME 274Ч216 , solution of ME 274Ч216
Chemical reaction 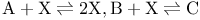 , complex Poisson rep. 283 284 , complex Poisson rep. 283 284
Chemical reaction 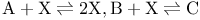 , Poisson rep. solution 279Ч281 , Poisson rep. solution 279Ч281
Chemical reaction 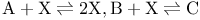 , positive Poisson re 288 , positive Poisson re 288
Chemical reaction 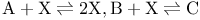 , spatially distributed 324 328 , spatially distributed 324 328
Chemical reaction 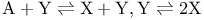 , elimination of intermediate 295 299 , elimination of intermediate 295 299
Chemical reaction 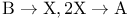 and positive Poisson re 288Ч289 and positive Poisson re 288Ч289
Chemical reaction 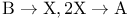 , complex Poisson re 284Ч285 , complex Poisson re 284Ч285
Chemical reaction 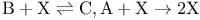 , spatially distributed 319 324 , spatially distributed 319 324
Chemical reaction 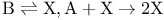 , analogy to harmonic oscillator 395 , analogy to harmonic oscillator 395
Chemical reaction 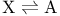 , and system size expansion 252 , and system size expansion 252
Chemical reaction 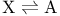 , master equation 238 , master equation 238
Chemical reaction 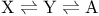 218 218
Chemical reaction 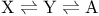 , chemical FPE 267Ч273 , chemical FPE 267Ч273
Chemical reaction  as reaction diffusion system 315Ч318 as reaction diffusion system 315Ч318
Chemical reaction 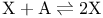 , chemical FPE 267Ч273 , chemical FPE 267Ч273
Chemical reaction 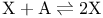 , FPE 127 , FPE 127
Chemical reaction  , reaction diffusion equations 314 , reaction diffusion equations 314
Chemical reaction  , solution of master equation 276Ч277 , solution of master equation 276Ч277
Chemical reaction, nonlocal 328
Chemical reaction, prey-predator system, FPE 268 273
Chemical reaction, unimolecular 279
Coherent states, Boltzmann master equation for 336Ч339
Coherent states, defined 375
Coherent states, expansion of an operator in 378
Coherent states, expansion of arbitrary states in terms of 377
Coherent states, Poissonian number distribution of 379
Coherent states, properties of 376 380
Collisions and flow 339Ч341
Combinatorial kinetics; defined 262
Commutation relations 373
Complex P-representation, defined 410
Complex P-representation, FPE from 416
Complex P-representation, operator identities for 414
Conditional probability 25
Conditional probability and eigenfunctions 13
Continuity in stochastic processes 45 46
Corrected Smoluchowski equation and escape problem 369
Correlation 30
Correlation functions of heat bath 389
Correlation functions, defined 33
correlation length 320
Correlation time 20 58
Correlations behaviour at instability point 323
Correlations behaviour of smooth functions of bath operators 389
Correlations behaviour, space-time 318
Covariance 30
Covariance matrix 30
Creation operator 373
Critical fluctuations 255
Critical slowing down 257
Cubic process 185
Cumulant 33 36
Cumulant generating function 33
Cumulant generating function, factorial 39
Cumulant, factorial 39
Density matrix 380Ч382
Density matrix, properties of 381 382
Destruction operator 373
Detailed balance 148Ч165
Detailed balance in birth-death master equation 237Ч238
Detailed balance in diffusion 307
Detailed balance, conditions for 151
Detailed balance, defined 148
Deterministic process 53
Differential Chapman Ч Kolmogorov equation 47Ч51
Differential Chapman Ч Kolmogorov equation, backward 55
Diffusion and detailed balance 307
Diffusion and detailed balance in a gravitational field 126
Diffusion and detailed balance in multivariate master equation 307 308
Diffusion and detailed balance, coefficient 5
Diffusion and detailed balance, current, defined 303
Diffusion and detailed balance, equation 5
Diffusion and detailed balance, inhomogeneous anisotropic 309
Diffusion master equation continuum form of 308Ч313
Diffusion master equation continuum form of system size expansion of 308
Diffusion matrix, defined 52
Diffusion process 52
Diffusion process, approximation by jump process 246Ч249
Divergence problems in nonlinear reaction diffusion systems 327
Double well potential 140
Double well potential, diffusion in 342Ч348
Drift vector, defined 52
| Eigenfunctions and autocorrelation matrix 168
Eigenfunctions and conditional probability 131 168
Eigenfunctions and exit time 172
Eigenfunctions and spectrum matrix 169
Eigenfunctions for FPE, variational principle for 168
Eigenfunctions for many-variable FPE 165
Eigenfunctions for one-variable FPE 129Ч136
Einstein equations and two-level atom 402
Ensemble average 17
Entrance boundary for FPE 123
Equilibration of populations in bistable system 348Ч357
Ergodic 17Ч18
Ergodic properties and stationary processes 57
Escape 342
Escape probability of particle in a double well 351
Escape time 141
Event 21
Existence theorems for P-representations 411 415
Exit boundary for FPE 123
Exit points, distribution of by asymptotic method 357 362
Exit time and eigenfunctions 172 (see also УFirst passage timeФ)
Exit time from a region, many variable FPE 170Ч171 (see also УFirst passage timeФ)
Exit time in a double well potential 345 (see also УFirst passage timeФ)
Exit time through a particular end of an interval 142 (see also УFirst passage timeФ)
Exit time, asymptotic analysis of 362 363
Factorial correlation in reaction diffusion system 315
Factorial cumulant 39
Factorial moment 38
Fast variable 197
FickТs law 303
FickТs law with fluctuations 304
First passage time for one dimensional FPE 136Ч142
First passage time for one dimensional FPE of particle in a double well 351
Flow and collisions 339 341
Flow as a birth death process 332Ч336
Flow in position space 334
Flow in velocity space 334
Fluctuating force 6 15
Fluctuation dissipation theorem 162
Flux, phenomenological 162
Fokker Ч Planck equation (FPE) 5 8 117Ч176
Fokker Ч Planck equation (FPE) from complex P-representation 416
Fokker Ч Planck equation (FPE) from P-representation 396 415
Fokker Ч Planck equation (FPE) from Poisson representation 278Ч285
Fokker Ч Planck equation (FPE) from positive P-representation 416Ч418
Fokker Ч Planck equation (FPE), backward, boundary conditions 128
Fokker Ч Planck equation (FPE), boundary conditions 118 125
Fokker Ч Planck equation (FPE), chemical 266
Fokker Ч Planck equation (FPE), connection with SDE 96
Fokker Ч Planck equation (FPE), defined 52Ч53
Fokker Ч Planck equation (FPE), functional 305
Fokker Ч Planck equation (FPE), many dimensional 143Ч170
Fokker Ч Planck equation (FPE), many variable, boundary conditions 146
Fokker Ч Planck equation (FPE), many variables, eigenfunctions 165
Fokker Ч Planck equation (FPE), one dimensional 117 143
Fokker Ч Planck equation (FPE), one variable, eigenfunctions 129Ч136
Fokker Ч Planck equation (FPE), small noise expansion for 187Ч194
Fokker Ч Planck equation (FPE), stationary solution for one variable 124
Fokker Ч Planck equation (FPE), Stratonovich form 100
Force, phenomenological 161
Fourier analysis of fluctuating functions 17
FPE (see Fokker УPlanck equationФ)
Functional derivative, defined 305
Functional FPE, for reaction diffusion systems 305 307
Gaussian distribution 36Ч38
Gaussian random variable 36
Generalised P-representations 408 419
Generalised P-representations and time development equations 415Ч419
Generalised P-representations, defined 409
Generalised P-representations, relation to Poisson representation 413
Generating function 13
Generating function for birth-death master equation 273 274
Generating function for Poisson distribution 38
Glauber Ч Sudarshan 382 384 410
Glauber Ч Sudarshan P-representation 382Ч384 410
HakenТs model 223
Harmonic oscillator, defined 374
Harmonic oscillator, driven by fluctuating field 398
Harmonic oscillator, driven damped 397 398
Harmonic oscillator, driven in P-representation 384
Harmonic oscillator, interaction with external field 375
Harmonic oscillator, quantum master equation 395 399
Harmonic oscillator, quantum mechanics of 373
Heat bath, defined 388
Hermite polynomials 134
Hermite polynomials in adiabatic elimination 202
Homogeneous Markov process 60
Homogeneous Markov process, defined 56
Independence 7 27
Independent random variables 27
Independent random variables and characteristic function 32
Interaction picture 394
Interaction picture and driven atom 399
Ito stochastic integral, defined 84
Ito stochastic integral, properties of 88 92
ItoТs formula, derivation of 95
Johnson noise 18 20
Joint probability 24
Jump process 52
Kramers Ч Moyal expansion 5
Kramers Ч Moyal expansion and system size expansion 251
Kramers Ч Moyal expansion in birth-death master equation 266
Kramers Ч Moyal expansion in Boltzmann master equation 337 340
Kramers Ч Moyal expansion, defined 249
KramersТ equation 155
KramersТ equation, boundary conditions 205
KramersТ method for escape problems 349Ч352
KramersТ method for escape problems in several dimensions 363Ч371
KurtzТs theorem 254
Laguerre polynomial 136
Langevin equation 11 14 80Ч83
Laplace transform and adiabatic elimination 200
Laser light scattering 7
Law of larse numbers 30
Limit almost certain 40
Limit almost certain in distribution 41
Limit almost certain in probability 41
Limit almost certain, mean square 40
Limit almost certain, stochastic 40
Limit of sequence of random variables 39
Lindeberg condition 37 46
Linear SDE multivariable 113
Linear SDE multivariable, single-variable 112
Liouville equation 53
Liouville equation, quantum 382
Liouville operators; defined 391
Local and global descriptions of chemical reaction, connection between 328Ч331
Local and global fluctuations 320
Markov assumption 13 43
Markov postulate 5 10
Markov process autocorrelation for 64Ч66
Markov process autocorrelation for continuous, defined 46
Markov process autocorrelation for continuous, homogeneous, defined 56
Markov process autocorrelation for continuous, quantum mechanical 373
Markov process autocorrelation for continuous, stationary, defined 56
Master equation 51 235Ч301
Master equation (cont.) quantum, derivation 390Ч394
Master equation, approximation by Fokker Ч Planck equation 246Ч257
Master equation, many-variable 262 277
Master equation, many-variable, Kramers Ч Moyal expansion for 266
Master equation, mean first passage times 259 262
Master equation, one-variable, stationary solution of 236Ч238
Master equation, phase space 331 341
Master equation, quantum; defined 394
Master equation, stationary solutions without detailed balance 266
Me (see УMaster equationФ)
Mean first passage time in one-variable FPE 137
Mean first passage time in one-variable FPE for master equations 259 262
Mean square limit in definition of stochastic integral 84
Mean value 28 29
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



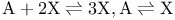
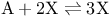 , in Poisson rep.
, in Poisson rep. 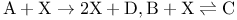 , solution of ME
, solution of ME 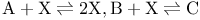 , complex Poisson rep.
, complex Poisson rep. 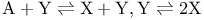 , elimination of intermediate
, elimination of intermediate 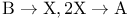 and positive Poisson re
and positive Poisson re 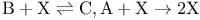 , spatially distributed
, spatially distributed 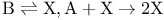 , analogy to harmonic oscillator
, analogy to harmonic oscillator 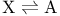 , and system size expansion
, and system size expansion 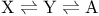
 as reaction diffusion system
as reaction diffusion system 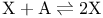 , chemical FPE
, chemical FPE  , reaction diffusion equations
, reaction diffusion equations