|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Kumpera A., Spencer D.C. — Lie Equations: General Theory. Vol. 1 |
|
|
 |
| Предметный указатель |
 -cohomology 34 83 85—86 -cohomology 34 83 85—86
 -complex 24 83 -complex 24 83
 -Poincare lemma 85—86 -Poincare lemma 85—86
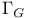 -structure 42 -structure 42
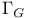 -structures, almost 7 9 -structures, almost 7 9
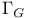 -structures, deformation of 30 33—35 -structures, deformation of 30 33—35
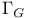 -structures, differentiable family of 30 31 -structures, differentiable family of 30 31
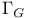 -structures, locally trivial family of 31 32 -structures, locally trivial family of 31 32
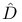 (linear operator), definition of 233 (linear operator), definition of 233
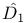 (non-linear operator), definition of 247 (non-linear operator), definition of 247
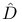 (non-linear operator), definition of 247 (non-linear operator), definition of 247
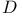 (non-linear operator), definition of 159 (non-linear operator), definition of 159
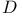 (non-linear operator), formula for 161 (non-linear operator), formula for 161
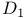 (non-linear operator), definition of 162 (non-linear operator), definition of 162
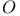 -algebra (left, right) 51 58 60 61 -algebra (left, right) 51 58 60 61
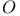 -module (left, right) 57 59 61 -module (left, right) 57 59 61
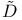 (linear operator), definition of 114 (linear operator), definition of 114
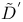 (linear operator), definition of 203 (linear operator), definition of 203
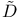 (non-linear operator), Buttin formula for 176 (non-linear operator), Buttin formula for 176
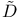 (non-linear operator), definition of 174 (non-linear operator), definition of 174
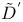 (non-linear operator), definition of 204 (non-linear operator), definition of 204
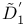 (non-linear operator), definition of 207 (non-linear operator), definition of 207
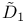 (non-linear operator), definition of 183 (non-linear operator), definition of 183
Actions of 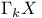 156 156
AD see also "Adjoint representation"
Ad (finite form of ad) in projective limit 255—256
Ad (finite form of ad), commutation with ad 178—179
Ad (finite form of ad), commutation with bracket 182
Ad (finite form of ad), definition of 170—171
ad as 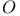 -linear sheaf map of Lie derivative 118—119 239—240 -linear sheaf map of Lie derivative 118—119 239—240
ad in projective limit 253
ad, commutation with Ad 178—179
ad, first definition of 117
ad, morphism of graded Lie algebras 241—242
ad, properties of 123
Adjoint representation 97
Adjoint representation, ad 116—117 239
Admissible derivations 215—216 217—218 220—222 224 225 226 227 228 232
Admissible derivations, strongly admissible 236—237 240
Admissible elements of 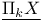 137 137
Admissible local maps 139 141
Admissible transformations 169 192 193
Admissible vector fields 90 140
Arens (R.) 13*
Ba (B.) 19*
Basis (left, right) 63
Beltrami equation 23
Bernard (D.) 24
Bers (L.) 23*
Bkouche (R.) 83
Bracket 104 see
Bracket in 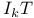 88 88
Bracket, ![$[ , ]_{\infty}$](/math_tex/4b7121d87efc6e5a850890f6f2eb36dc82.gif) 253 253
Bracket, commutation of [ , ] with Ad 182
Bracket, invariance of [ , ] 177
Bracket, [ , ] 107
Buttin (C.) vii 43 176
Buttin formula 176
Campbell — Hausdorff formula 268
Canonical transformations 40
Cartan (E.) 26 230
Cartan (H.) 22
Cartan formula (for Lie derivative) 230
Cartan — Kaehler theory 26
Characteristic ideal 44
Characteristic variety 44 46
Chern (S.S.) 23 24
Cohen — Macaulay equation (structure) 43—44
Complex analytic structure 46
Complexes, 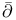 -complex 24 83 -complex 24 83
Complexes, 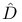 -complex 233 235 -complex 233 235
Complexes, 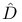 -complex in the projective limit 254 -complex in the projective limit 254
Complexes, 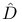 -complex 246 -complex 246
Complexes, 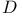 -complex in the projective limit 255 -complex in the projective limit 255
Complexes, first linear complex 4 64 66
Complexes, first non-linear complex 4 159 162
Complexes, fourth non-linear complex (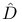 -complex) 247 -complex) 247
Complexes, non-linear complex for groupoids 275—276
Complexes, non-linear complex in deformation theory 34
Complexes, principal symbol complex 44
Complexes, restricted 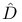 -complex 245—246 -complex 245—246
Complexes, second linear complex 4 75 76 86
Complexes, second non-linear complex 4 177 183 188 195
Complexes, third non-linear complex 4 7 202 207
Connections, Levi-Civita connections 11 25
Connections, linear connections 11
Contact elements 9
coordinates 61 98 142
Courant (R.) 23*
D (linear operator), characterization of 75
D (linear operator), definition of 66
D' (linear operator), definition of 76
Darboux (G.) 12 13 41
de Barros (C.M.) viii 19 28
de Rham (G.) 3 4 15 20 28 29
Deformation of  -structure 39 -structure 39
Deformation of 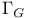 -structure 42 -structure 42
Deformation of complex analytic structure 46
Deformation of Lie structure 33—35
Deformation of multifoliate structure 42
Deformation of symplectic structure 40
Deformation of volume structure 38
Deformation theory of Lie structure 29
Deformation theory of Lie structure, general mechanism for 33—35
Deformation, germs of 34
Derivations of 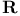 -Lie algebra ( -Lie algebra (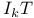 , [ , ]) 97 , [ , ]) 97
Derivations of jet forms 212
Derivations of scalar differential forms 104
Derivations, admissible 215—218 220 222 224—228 232
Derivations, decomposition of 106 228
Derivations, formulas for brackets of 232
Derivations, interior 105 216 222—224 233
Derivations, Lie 106 117 216 225—227
Derivations, strongly admissible 236—237 240
Diagonal 52 272
Diagonal approach 139
Diagonal module (submodule) 89—90
Diagonal structure 88—92 108—109 111
Diagonal, ideal of 53
Diagonal, reflection on 54 59
Differential equations (homogeneous linear partial) 77 79
Differential forms (canonical) 11
Differential operators (linear) 87
Dolbeault (P.) 21—22
Dolbeault complex 21 22 46—47
Eckmann (B.) 20 22*
Ehresmann (C.) vi 16 18 20 22 24 26* 52 138 257 270
Eliopoulos (H.A.) 28
Exponential map (Exp) for Lie groupoid 261
Exponential map (Exp), bijectivity of 201
Exponential map (Exp), definition of 144—145
Exponential map (Exp), differentiability of 147
Finite type 25 27
Formally integrable (differential) equation 83—84 86
Forms, horizontal (vertical) 64 109—110 126
Frames, admissible 6
Frames, fields of 10
Frechet derivative 70 158
Frobenius integrability condition 14 25
Frobenius integrability condition, complex 21
Frobenius theorem 9—11 13
Frobenius theorem, complex 20 22—24
Froelicher (A.) 14* 15* 20 22* 104* 223*
Froelicher — Nijenhuis resolution 246
Froelicher — Nijenhuis theory 104 212 216 233
Fundamental identities for 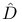 , , 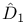 252 252
Fundamental identities for 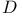 , , 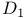 164—165 164—165
Fundamental identities for 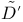 , , 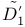 210—211 210—211
Fundamental identities for 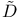 , , 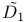 184—186 184—186
Fundamental identities for brackets of derivations 232
| Fundamental identities for D, 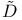 (and brackets) 124 (and brackets) 124
Generalized differentiable manifold 54
Godbillon (C.) 13*
Goldschmidt (H.) 80 83—85
Goursat (E.) 13*
Graded Lie algebra 112 114 121 221 223 255
Gray (J.W.) 13*
Griffiths (P.A.) 29
Grothendieck (A.) v
Groupoid 8 29 33 257 see
Groupoid of invertible elements 136 137 141
Groupoid, differentiable 258
Gugenheim (V.K.A.M.) 13* 15* 21*
Guillemin (V.W.) 4 25 26 44 45* 170
Haantjes (J.) 14
Hilbert (D.) 23*
Hoermander (L.) 22 24* 45
Holonomic elements (left, right) 63 77 80 87 95
Homological length 45
Homotopy operator 73
Horizontal (vertical) projection 126
Horizontal differentiation 68
Infinite type 26
Infinitesimal deformation 32—33
Infinitesimal neighborhood (of diagonal) 53 56
Infinitesimal transformations 6 40 42
Integrability condition 9—10 14—15 21 22 24
Integrability of 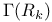 -structure 7 -structure 7
Integrability of almost  -structure 7 9 -structure 7 9
Integrability of field of contact elements 9
Integrability of Lie structure 7
Integrability, formal 80 83—84 86
Integrable almost  -structure 7 9 -structure 7 9
Integrable equation 80
Integrable G-structure 6
Integrable structure 8
Integral submanifold 9
Interior derivations 105 216 222—224 233
Involutive equation 26
Involutive systems 26 83
Isothermal parameters 23
Jacobi identity 105 116 120 121 131 134 183 233
Jet bundles 50
Jet forms 212
Jet sheaves, linear 49
Jet sheaves, non-linear 136
Klemola (T.) viii
Kobayashi (E.T.) 27 104* 223*
Kodaira (K.) 32* 33* 36 42* 43* 48
Kohn(J.J.) 22
Korn (A.) 23
Kumpera (A.) 3* 271*
Kuranishi (M.) 48
Lehmann (D.) 80
Lehmann-Lejeune (J.) 27 28*
Levi-Civita (T.) 11 25
Libermann (P.) 5 22* 27
Lichnerowicz (A.) 13*
Lichtenstein (L.) 23
Lie (S.) 5
Lie algebra of groupoid 144 260
Lie algebra, graded 112 114 121 144 221 223 255
Lie derivations 106 117 216 225—227
Lie derivative 10 37 88 118—119 217 230 239—240
Lie equations 33 37 43 46
Lie equations, elliptic v 3 7
Lie equations, linear 5 6 7 10 14 30 88 100 102
Lie equations, non-linear 6 7 8 30
Lie groupoid 6 257 259
Lie groupoid, prolongation of 269
Lie pseudogroup 6
Lie structures 7 33 43
Lie structures, deformation of 29 33—35
Lie structures, elliptic 22
Local rings (sheaf of) 49
Local solution (of differential equation) 80
Locally universal family 41
Malgrange (B.) v vi vii 4 7* 22 24* 26 27 36 53 83 102 138 170 251
Matsushima (Y.) 24
Model category 30
Model category, 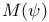 37 37
Multifoliate group (structure) 42—43
Neumann problem 45
Newlander (A.) 22 27 36
Ngo Van Que 4 271 275
Nickerson (H.K.) 13 15* 21*
Nijenhuis (A.) 14* 15* 22 24 104* 223*
Nijenhuis bracket 4 14 20 48 107 112 114 115 117 131 134 159 169 216 227 230 238 239 246 253
Nijenhuis torsion tensor 24 27
Nilpotent elements 54
Nirenberg (L.) 22 23 24* 27 36 48*
Parallelism 10
Partial exactness of second non-linear complex 188 195
Partial exactness of third non-linear complex 208
Poincare complex 45
Poincare lemma 15 21 28 40 69 73 85
Pradines (J.) 261
Projective limits 252
Prolongation of differential equations 80
Prolongation of Lie equations 103
Prolongation of Lie groupoids 269
Prolongation of maps 79
Prolongation of sheaves 55
Prolongation space 52 54
Pseudodifferential operators 45
Pseudogroup, continuous 7 8
Pseudogroup, primitive 36
Pseudogroup, simple 36
Pseudogroup, transitive (continuous) 35 42
QUE see "Ngo Van Que"
Quillen (D.G.) 83
Regular functions 42
Regular maps 29
Restriction map 32
Samelson (H.) 23*
Schouten (J.A.) 13
Semi-holonomic jets 27
Singer (I.M.) 24 25 26
Solutions (sheaf of) 87
Source (target) maps 136—137 272
Spencer (D.C.) v vi vii 3 7* 13 15* 21* 26 27 32* 33* 36* 38* 42* 43* 47* 48* 80 242 246 248 251
Split exact 50
Split injective 60
Stable cohomology (range) 86
Sternberg (S.) 4 13* 24 25 26 44 45* 170
Structive tensor 24
Structive tensor of higher order 25—27
Structure equations 3 162 177 183 207 208 247 256
Structures, 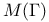 -structure 30 -structure 30
Structures, 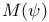 -structure 37 -structure 37
Structures,  -structures 7 9 30—35 -structures 7 9 30—35
Structures, 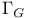 -structures 42 -structures 42
Structures, almost  -structures 7 9 -structures 7 9
Structures, almost-complex 7 15 19 23
Structures, almost-product 13—14
Structures, almost-symplectic 18—19
Structures, Cohen — Macaulay 43
Structures, complex analytic 42 46
Structures, conformal 26
Structures, contact 12 36
Structures, defined by differential forms 37
Structures, defined by fields of endomorphisms 27
Structures, defined by fields of p-frames 10
Structures, defined by linear connections 11
Structures, diagonal 88—92 108—109 111
Structures, elliptic almost-structures 8
Structures, foliate 42
Structures, G-structures 5 6 8 9 10 24
Structures, left (right) 51—53 56 59 77
Structures, Lie 7 22 29 33—35 43
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -cohomology
-cohomology 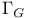 -structure
-structure 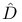 (linear operator), definition of
(linear operator), definition of 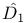 (non-linear operator), definition of
(non-linear operator), definition of 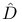 (non-linear operator), definition of
(non-linear operator), definition of 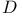 (non-linear operator), definition of
(non-linear operator), definition of 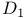 (non-linear operator), definition of
(non-linear operator), definition of 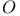 -algebra (left, right)
-algebra (left, right) 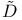 (linear operator), definition of
(linear operator), definition of 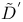 (linear operator), definition of
(linear operator), definition of 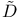 (non-linear operator), Buttin formula for
(non-linear operator), Buttin formula for 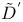 (non-linear operator), definition of
(non-linear operator), definition of 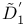 (non-linear operator), definition of
(non-linear operator), definition of 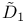 (non-linear operator), definition of
(non-linear operator), definition of 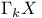
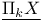
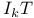
![$[ , ]_{\infty}$](/math_tex/4b7121d87efc6e5a850890f6f2eb36dc82.gif)
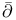 -complex
-complex  -structure
-structure 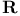 -Lie algebra (
-Lie algebra (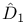
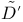 ,
, 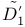
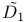
 -structure
-structure 
 -structure
-structure