|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Eisenhart L.P. Ч Continuous groups of transformations |
|
|
 |
| ѕредметный указатель |
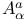 , , 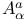 , ,  , , 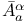 20Ч23 27Ч30 32 161 198Ч201 206 206 229 20Ч23 27Ч30 32 161 198Ч201 206 206 229
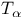 14 14
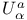 , ,  , ,  , ,  51Ч55 51Ч55
Abelian group 48Ч50 86 88 113 137 166 160 162 183 184 192 218Ч220 227
Absolute, invariant of a group 61 62 67 68 93 96 96 107
Adjoint group 151Ч166 160Ч163 170 183 199
Affine group 43 67 66
Affine group, parameter 199
Amaldi 267 296
ARC 199 212
Asymmetric connection 197 198 230 234
Asystatic group 84 86 123
Automorphism, 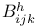 196Ч198 232 233 196Ч198 232 233
Automorphism, 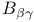 206 206
Automorphism, of a group 151
Automorphism, of a space 230 231 236
B her 69 146 177 294 her 69 146 177 294
Base, vector 141
Base, vector, change of 141 142
Basis of a function group 282 285 288
Basis, change of 28
Basis, of a group 28
Berwald 277 295
Bianchi 26 44 66 66 71 82 86 108 121 123 133 137 138 212 216 218 220 228 229 236 293 294
Bianchi, identity of 232
BOM 280 296
Bortolotti 237 296
Burnside 183 294
Burnside, 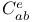 22 26 27 22 26 27
Burnside, 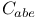 162 206 162 206
Canonical form of a function- group 286 290
Canonical, form of transformation 145Ч160
Canonical, parameter 46 47 62 160 161 160
Cartesian coordinates 188
Carton 66 167 169 173 174 179 180 182 184 199 201Ч208 213 236 237 293Ч296
Characteristic, equation 140Ч142 165Ч160 164 169 172 177-179
Characteristic, function 262 260 262 274 278 280 292
Characteristic, matrix 166
Christoffel symbol 188 236
Classification of groups 166 180Ч182
Clifford, parallelism of 237
Coefficient of linear connection 47 192
Cohen 91 294
Comitant 161
Commutative, 113
Commutative, function-groups 283 287 288 290
Commutative, functions 283
Commutative, groups 112 114Ч117 121 122 256
Commutative, transformations 110 112
Commutator 6
Complete system of differential equations 7 8 12 86
Completely integrable differential equations 1 4
Complex, linear 186
Composition, constants of 22
Composition, indices of 128
Composition, series of 127Ч134
Conformal spaces 236
Connection, 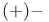 199 230 199 230
Connection, 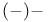 199 230 199 230
Connection, (0)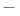 199 206 231 199 206 231
Connection, asymmetric 197 198 230 234
Connection, coefficients of 47 192
Connection, linear 45 47 192
Connection, symmetric 194 198 233 234 236
Constant, of composition 22
Constant, of composition of structure 22 26 28 43 48 56 112 126 151
Contact transformation, geometrical properties 242Ч246 267 267Ч277
Contact transformation, geometrical properties of maximum rank 263Ч273 276
Contact transformation, geometrical properties, homogeneous 239Ч266 263Ч278 291 292
Contact transformation, geometrical properties, infinitesimal 251Ч266 260 262 281 292
Contact transformation, geometrical properties, non- homogeneous 255Ч263 281
Contact transformation, geometrical properties, restricted non-homogeneous 260Ч263 280 281 286 287 291
Continuous group, finite 16 17
Continuous group, finite, infinite 15
Continuous group, finite, mixed 68
Contravariant, tensor 187
Contravariant, vector 26 36 187
Cosine of angle 209 212
Covariant, derivative 189
Covariant, differentiation 189 196 198 232 233
Covariant, normal 239 242Ч244 246
Covariant, tensor 187
Covariant, vector 27
Curvature, 195Ч198 206 207
Curvature, of a curve 98
Curvature, of a curve, 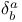 8 8
Curvature, tensor 188
Derivative, covariant 189
Derived group 132Ч135 154 164 169 173 184
Dickson 15 91 294
Differential equations of a group 20
Differential equations of definition of a group 56 57
Differential equations of second order 100 107 108
Differential equations, admitting a group 82 86 88 89 95 96 100 101 107 135
Differential equations, admitting linear operators 85Ч91 106Ч108
Differential equations, associated 5 9
Differential equations, complete 7 8 12 86
Differential equations, completely integrable 1 4
Differential equations, linear partial 7 12 63 82 85Ч88
Differential equations, mixed 4
Differential equations, ordinary of first order 89 95Ч97
Differential equations, Pfaffian 93Ч95
Differential equations, system of 1 7
Differential equations, total 1
Differential invariant 96Ч98 100Ч107
Differentiation, covariant 189 195
Differentiation, covariant, 232 233
Dilatation 42
Direct product of groups 120Ч122 174 184
Displacement, parallel 199
Distance 191
Dummy index 7
Dynamics 277Ч280
Dynamics, 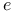 186 186
Dynamics, 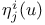 60 152 60 152
Eiesland 236 295
Einstein 196 295
Einstein space 206
Eisenhart 80 199 236 239 294Ч296
Elementary, divisor 146
Elementary, hyperplane 238
Elementary, hypersurface 267
Engel 54 91 164 293 296
Envelope 244 245 268 271 272
Equations, of a group 13 16 20 56 57
Equations, of a motion 209
Equipollent vectors 201Ч203 207 208
Equivalent function-groups 287 291
Equivalent groups 34 76Ч80 84 115
Equivalent points 67
Essential parameters 9Ч12 56
Euclidean space 186 188 190 191
Euclidean space, 208 212 218
Exceptional 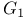 of a of a  113 118 152 162 183 113 118 152 162 183
Extended group 92Ч97 107 252
Extension of a group 97Ч101 105 125
Factor group 129Ч131 137
FermatТs principle 280
Fine 13 15 243 246 258 264 294 295
Finsler 277 294
Flat space 188 193 203Ч205
Franklin 91 295
Frobenius 183 294
Fubini 217 218 221 229 294
Function group, basis of 282 285Ч291
Function group, commutative 283 287 288 290
Function group, equivalent 287 291
Function group, homogeneous 287Ч292
Function group, non-homogene- ous 281Ч287 291 292
Function group, reciprocal 283 285 288 290 291
| Function group, subgroup of 282Ч286 290
Functions, commutative 283
Functions, in involution 250 283
Functions, singular 283 284 287 291 292
Fundamental theorem, 216 277
Fundamental theorem, 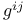 188 189 194 195 188 189 194 195
Fundamental theorem,  60 61 90 91 135 137 155 184 228 60 61 90 91 135 137 155 184 228
Fundamental theorem, 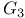 66 67 123 133 137 138 154 184 227 236 255 66 67 123 133 137 138 154 184 227 236 255
Fundamental theorem, 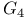 66 123 136 137 155 184 66 123 136 137 155 184
Fundamental theorem, 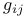 156 174 186Ч189 194 195 205 156 174 186Ч189 194 195 205
Fundamental theorem,  17 17
Fundamental theorem,  44 194 199 206 231Ч233 44 194 199 206 231Ч233
Fundamental Theorem, First 24
Fundamental Theorem, Second 54
Fundamental theorem, third 55
Fundamental, 208 226 236
Fundamental, quadratic form 186
Fundamental, tensor 187 195
Fundamental, variety 244
Fundamental, vector 148 166 170
Generic, rank 49 64
Generic, root 156 160
Geodesic 191 193 206 207 209Ч212 216 217 235 274Ч277 279
Geodesic, correspondence 236
Geodesic, hypersphere 275 279
Geodesic, sub-space 203
Geodesically parallel hypersunaces 211 235
Graham 182
Group 14
Group, admits a transformation 110 112 121
Group, basis of 28
Group, finite continuous 16 17
Group, generator of 40
Group, infinite 15 249
Group, infinitesimal transformation of a 36 40 41
Group, invariant under a transformation 110Ч112 121
Group, mixed 58
Group, one- parameter 32Ч36
Group, rank of a 159 160
Group, semi 15 17 18 21 28 29 31
Group, structure of a 28
Group, symbols of a 28
Group, trajectories of a 35 40 44 45 253 274 affine asystatic derived extended extension factor imprimitive induced integrable intransitive linear motion primitive projective semi-simple simple systatic transitive)
Group-space 27 31 44Ч47 198Ч206
Group-space, 213 229Ч231 236
Groups with the same structure 28 29 32 76 78 80 93 98 125 equivalent isomorphism reciprocal)
Groups, classification of 165 180Ч183
Groups, classification of, product of 120Ч122 174 184
Groups, similar 76
Hamiltonian equations 263 279
Hamiltonian equations, function 263 279
Holonomic system 263 277
Homothetic transformation 42
Huntington 15 294
HuygenТs principle 272
Hyperplane 238
Hyperplane, tangential 239 267
Hypersphere 275 279
Hypersurface 210 237
Hypersurface of origin 271 272
Hypersurface, elementary 267
Hypersurface, geodesically parallel 210 211 235
Identity 15
Identity of Bianchi 232
Identity of Jacobi 6 250
Identity of Ricci 189 232
Identity, transformation 14
Imprimitive group 80Ч83 117 123 137
Imprimitivity, system of 80Ч85 117 137
Independent (cpnstant coefficients) 21
Indices of composition 128
Induced group 70Ч72 84 85 119 123 124 137Ч139
Infinitesimal, motion 208 209 231
Infinitesimal, motion, transformations of a group 36 40 41
Integrable group 134Ч137 144 145 162Ч165 172 173 183 184
Intransitive group 71Ч73 78Ч80 98
Intransitive group, 210 216Ч226 235 236
Invariant of points 108
Invariant sub-group 118Ч124 129Ч134 137Ч139 144 153 154 158 161Ч163 173 174 183 184 203 235
Invariant sub-group, maximum 122 127Ч131
Invariant variety 67Ч72 80 81 85
Invariant variety, 123 138 153 210 211
Invariant variety, isolated 119
Invariant variety, minimum 67Ч71 211 221 235
Invariant vector-spaces 142Ч145 163
Invariant, absolute, of a group 61 62 67Ч69 93 95 96 98 107 159 161
Invariant, differential 96Ч98 100Ч107
Invariant, direction 140 142 144
Invariant, numerical 291
Invariant, relative, of a group 63 66 67 69 93 95 107
Inverse transformation 13 249
Inverse transformation of a semi-group 17
Involution, functions in 250 283
Isolated variety 119
Isomorphism of groups, simple 124Ч127 131 137 151 208
Isomorphism of groups, simple, multiple 124Ч127 129 136 151 184
jacobi 263 293
Jacobi, form of a complete system 8
Jacobi, identity 6 250
Jacobi, relations 26
Killing 158 164 180 183 184 208 293
Killing, equations of 208 215Ч221 237
Knebelman 236 295 296
Kronecker delta 8
Kronecker delta, 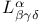 198 198
Kronecker delta,  29 198 199 229 29 198 199 229
Kronecker delta, 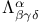 75 193 195 75 193 195
Kronecker delta, 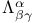 74 192Ч197 217 218 230 74 192Ч197 217 218 230
Lagrangian function 263 278
Length, element of 186
Levi Ч Civita 190 267 294 295
Lie 36 39 54 55Ч58 66 80 84 91 106Ч108 119 122 123 131 137 145 154 155 163 164 180 183Ч185 242 248Ч252 255 258Ч261 278 281 282 285 287-292 293
Lie group 40
Linear, complex 185
Linear, complex, group 43 138 143Ч150 153 163 184 234 292
Matrix, characteristic 155
Matrix, equation 142Ч144 148Ч150
Matrix, trace of a 157
Mattoli 194 295
Maurer 23 293
Maximum invariant sub-group 122 127Ч131
Metric, generalized 277
Metric, Riemannian 187 206
Michal 43 295
Minimum invariant variety 67Ч71
Minimum invariant variety, 221 223 235
Mixed, group 58
Mixed, system of differential equations 4
Moore 15 294
Motion, in 2Чspace 42 80 98 226Ч228
Motion, in 3Чspace 43 80 228
Motion, infinitesimal 209
Motions, group of 57 208Ч221 230Ч237
Motions, in a linearly connected manifold 229Ч235 237
Motions, intransitive 210 216Ч226 235 236
Motions, multiply transitive 221
Motions, of maximum order 215 224 236
Motions, simply transitive 218 235 236
Multiply isomorphic groups see Isomorphism
Normal, covariant 239 242 243
Null vector 174 187 212
Null vector, 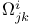 195Ч198 205Ч207 231Ч235 237 195Ч198 205Ч207 231Ч235 237
Operator, linear 6
Parallelism, 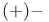 199Ч205 199Ч205
Parallelism, 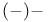 199Ч205 199Ч205
Parallelism, (0)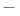 199 204 205 199 204 205
Parallelism, absolute 190 193 194
Parallelism, absolute, 217 234 235
Parallelism, relative 190 191 193 199
Parameter affine 199
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



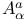 ,
,  ,
, 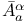
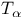
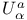 ,
,  ,
,  ,
, 
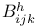
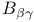
 her
her 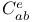
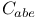
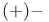
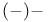
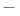
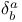
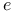
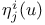
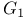 of a
of a