Авторизация
Поиск по указателям
Reed M., Simon B. — Methods of Modern mathematical physics (vol. 4) Analysis of operators
Обсудите книгу на научном форуме Нашли опечатку?
Название: Methods of Modern mathematical physics (vol. 4) Analysis of operatorsАвторы: Reed M., Simon B. Аннотация: The book covers the theory about eigenvalues of Schrodinger operators. It is complete success in explaining clearly the basic concepts involved: perturbation theory (summability questions, fermi golden rule), min-max principle for discrete spectrum, Weyl theorem, HVZ theorem, the absence of singular continuous spectrum, ground state questions, periodic operators, semiclassic distribution of eigenvalues, compactness criteria.
Язык: Рубрика: Математика /Математическая Физика /Учебники /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1978Количество страниц: 396Добавлена в каталог: 24.04.2005Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Operator, non-self-adjoint 316—338 Operator, norm Operator, normal Operator, positive 195 Operator, positivity improving 201 Operator, positivity preserving 201 Operator, relatively bounded Operator, relatively compact 113 Operator, relatively form bounded Operator, relatively form compact 369 Operator, resolvent Operator, Schrodinger 79 Operator, self-adjoint Operator, smooth 142 Operator, symmetric Operator, tensor product Operator, topologies Operator, trace class Operator, unbounded, general theory Order k strong asymptotic series 43 O’Connor — Combes — Thomas theorem 198 O’Connor’s lemma 196 Paley — Wiener theorems Parseval’s relation Part of the spectrum in X 46 Partial trace 382 Period cell 303 Periodic potentials 279 Perron — Frobenius theorems 202 350 Perturbation series 2 Perturbation series, asymptotic 26 Perturbation series, Puiseux 4 Perturbation series, Raleigh — Schrodinger 1 Perturbation series, strong asymptotic 40 Perturbation series, wildly divergent 27 Phase space Phragmen — Lindelof principle 236 Plancherel theorem Plemelj — Smithies formulas 332 Poisson bracket Poisson summation formula 380 Polar decomposition Polarization identity Positive definite see also “Positive type” Positive definite, conditionally 214 Positive distribution Positive function 201 Positive operator Positive type, distribution Positive type, function Positivity improving operator 201 Positivity preserving operator 201 Principle of uniform boundedness Product formula Projection Projection valued measure (p.v.m.) Pseudo-eigenvalue 48 Pseudo-eigenvector 48 Puiseux series 4 Putnam — Kato theorem 157 Quadratic forms Quadratic forms, closed Quadratic forms, form core Quadratic forms, form domain Quadratic forms, Friedrichs’ extension Quadratic forms, infinitesimally bounded Quadratic forms, positive Quadratic forms, relatively bounded Quadratic forms, relatively compact 369 Quadratic forms, Riesz lemma Quadratic forms, semi-bounded Quadratic forms, strictly m-accretive Quadratic forms, strictly m-sectorial Quadratic forms, symmetric Radius of gyration 197 Radon — Nikodym theorem Rayleigh — Ritz technique 82 Rayleigh — Schrddinger coefficients 5—8 Rayleigh — Schrddinger series 1 5 Rayleigh’s theorem 364 Reduced disconnected part 131 Reduced resolvent 130 Relatively bounded Relatively compact 113 Relatively form bounded Relatively form compact 369 Rellich’s criterion 247 Rellich’s theorem 4 Resolvent Resolvent set Resonance eigenvalues 191 Resonance pole 55 Resonance thresholds 191 Retardation term 81 Riccati equation 96 Riemann — Lebesgue lemma Riesz’s criterion 248 Riesz’s lemma Rollnik potential Scale of spaces Schrodinger equation Schrodinger operators 79 Schur basis 318 Schur — Lalesco — Weyl theorem 318 Schwartz space Schwarz inequality Secular equation 2 Segment property 256 Self-adjoint operator, bounded Self-adjoint operator, unbounded Semibounded operator Semibounded quadratic form Semigroup, Semigroup, contraction Semigroup, holomorphic Semigroup, hypercontractive Semigroup, infinitesimal generator Semigroup, strongly continuous Singular support Singular value of a compact operator Smooth operator 142 Sobolev inequality Sobolev lemma Sobolev spaces 253 Solid state theory 311 Sommerfeld correction 80 Spectral concentration 45—50 Spectral mapping theorem 109 181—183 Spectral measures Spectral measures, associated with a vector Spectral projections Spectral theorem, functional calculus form Spectral theorem, multiplication operator form Spectral theorem, p.v.m. form Spectrum 118 Spectrum,absolutely continuous Spectrum,approximate point 178 Spectrum,asymptotically in a set 46 Spectrum,continuous Spectrum,continuous singular Spectrum,discrete 13 Spectrum,essential Spectrum,point Spectrum,residual Spin-orbit correction 80 Spin-spin interaction 81 Stable eigenvalue 29 Standard 271 Stark effect 50 118 Stone’s formula Stone’s theorem Strichartz’s theorem 378 Strictly m-accretive form Strictly m-accretive operator Strictly m-sectorial form Strictly positive function 201 String 129 Strong asymptotic series 40 Strong operator topology Strong resolvent sense, convergence in Strongly continuous semigroup 235 Strongly continuous unitary group 265 Strongly measurable Sturm oscillation theorem 92 Summability methods, Borel 44 Summability methods, Pade 63 Summability methods, regular 63 Support of a distribution Support of a distribution, singular Symmetric operator Symmetric quadratic form Tempered distributions Temple’s inequality 84 Temple’s inequality, generalized 365 Tensor product, Hilbert spaces Tensor product, operators Tensor product, spectrum of 177 Time-dependent perturbation theory 51—60 66—68 Total mass 197 Trace class 207— Trotter product formula Trotter — Kato theorem Uncertainty principle lemma Uniform boundedness principle see “Principle of uniform boundedness” Uniform operator topology Uniformly Holder continuous 191 Uniformly locally 302 Unique continuation 226 239 Unitary operator Virial theorem 231 von Neumann’s theorem von Neumann’s uniqueness theorem Watson’s theorem 44 Weak derivative Weak graph limit Weak topology Weak- Weak- Weakly measurable (vector-valued) function Weighted 168 Weinberg kernel 125 Weinberg kernel, symmetrized 131 Weinberg — Van Winter equation 126 Weyl relations Weyl’s criterion Weyl’s lemma Weyl’s theorem, classical 117 Weyl’s theorem, essential spectrum 112 Width of a resonance 55 Wiener measure Wiener measure, conditional 102 Wigner — Seitz cell 311 Wigner — von Neumann potential 223 wronskian Young’s inequality 282 Zhislin’s theorem 89
Реклама
 |
|
О проекте
|
|
О проекте



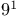
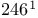
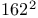
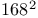
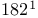 —
—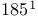
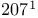 —
—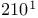
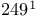 —
—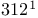
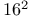
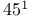 —
—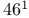
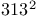
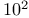
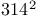
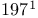
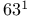
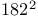
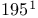
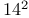
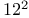
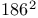
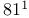
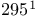 —
—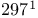
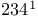 —
—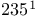
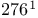
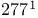
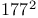
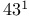
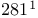
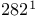
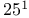
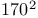
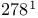
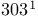
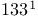
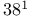
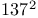
 -contractive
-contractive 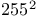
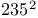
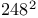
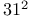
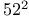
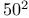
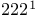
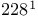
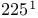
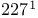
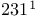
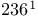
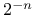 cube
cube 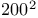
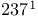
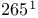 —
—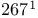
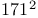
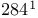 —
—










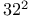

 space
space 


