|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Курант Р., Гильберт Д. — Методы математической физики (том 1) |
|
|
 |
| Предметный указатель |
Полнота системы собственных функций дифференциального уравнения 339 331—342 347 402
Полнота системы соотношение или условие полноты 4 46
Полнота системы степеней 58—61
Полнота системы тригонометрических функций 61—62
Полнота системы шаровых функций Лапласа 487
Полнота системы штурм-лиувиллевских собственных функций 339
Полярное интегральное уравнение 149
Полярные координаты, преобразование 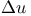 к полярным координатам 216—217 к полярным координатам 216—217
Потенциал логарифмический 355
Потенциал Ньютона 354—355
Потенциал, теория потенциала 166—171 297—306 342—348 354—366
Потенциал, уравнение потенциала 182
Предельные точки, принцип предельных точек 52
Преобразование бесконечно большого числа переменных 48—49
Преобразование бесконечно малое линейное 35—36
Преобразование вариационных задач 222—233
Преобразование дифференциального выражения 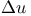 216 216
Преобразование интегральное п. Мелина 95—98
Преобразование интегральное, преобразование дифференциального уравнения 444—445 446 481—485
Преобразование квадратичной формы к главным осям 20—30
Преобразование Лапласа 445 454
Преобразование линейное 5 и след.
Преобразование ортогональное 12—14 48—49
Преобразование унитарное 14
Преобразование Фридрихса 225 226
Преобразование Эйлера 445
Преобразование, формула преобразования тета-функции 68—69
Продольный изгиб 258
Произведение скалярное векторов 1—2
Произведение скалярное функций 42
Производящие функции 452 453 483 485
Пространство функций 51
Прямые методы вариационного исчисления 162
Пуассон, интеграл Пуассона 488—489
Пуассон, уравнение Пуассона 346
Пуассон, формула суммирования Пуассона 69
Равностепенная непрерывность 52 105
Разложение, теоремы о разложении 339—340 342 347 348 349 373 404—407 488
Разрешающее ядро 130 131
Разрыв, условия разрыва 381
Резольвента билинейной формы 16
Резольвента квадратичной формы 26—28
Резольвента линейного интегрального уравнения 130 135
Рисса-Фишера теорема 102
Ритц, метод решения вариационных задач 163—165
Ряд Неймана 8 16 130 320
Ряд Фурье 62—70
Свет, кратчайшее время распространения света, принцип Ферма 153
Световые лучи 153 158 179 205 243
Свободные края, свободная вариация на границе 198—201
Сильвестр, алгебраическая теорема Сильвестра 493 494—496
Сильвестр, выражение шаровых функций Максвелла — Сильвестра 489—496
Симметризация, ядро, допускающее симметризацию 150
Симметрическое ядро 113—124
Скалярное произведение векторов 1—2
Скалярное произведение функций 42
Собственная частота 268 272
Собственные векторы 21 268
Собственные значения 15 23—24 113—124 272 292 375
Собственные значения бесконечно большой кратности 372
Собственные значения кратные 120
Собственные значения, задачи о собственных значениях см. «Задачи о собственных значениях»
Собственные значения, их распределение 385—402 407—423
Собственные значения, их существование 28—30 113—124 338 341—342 347 348
Собственные значения, максимально-минимальное свойство 28—30 122—124 383
Собственные значения, оценки 439—441
Собственные значения, экстремальные свойства 375
Собственные колебания 268 272
Собственные функции 105 272
Собственные функции, их существование 338 341—342 347 348—349
Сопряженное дифференциальное выражение 262—265
Сосредоточенная сила 331 342
Спектр дискретный, имеющий конечную точку сгущения 322—324
Спектр дифференциального уравнения 320 321
Спектр матрицы 15
Спектр непрерывный 92—93 320—324 426
Спектр унитарной матрицы 39—40
Спектральное разложение 92—93
Стационарные функции и кривые 176
Стержень однородный 279
Стержень, вариационная задача и дифференциальное уравнение 237
Стержень, естественные краевые условия 237
Стержень, задача о собственных значениях 279—281
Стержень, потенциальная энергия 237
Стирлинг, формула Стирлинга 496—498
Струна неоднородная 275—279
Струна однородная 271—275
Струна оттянутая 366—367
Струна, вариационная задача и дифференциальное уравнение 236
Струна, потенциальная энергия 236
Струна, примеры на колебание струны 366—368
Суммирование, формула суммирования Пуассона 69
Суммируемые функции 100
| Суперпозиция, принцип суперпозиции 261
Сходимость в среднем 102
Сходимость, теоремы сходимости Лебега 101
Тензор Грина 371
Теплопроводность, задачи о собственных значениях в теории теплопроводности, дифференциальное уравнение теплопроводности 294—295
Тета-функции, применения 360—362 366
Тета-функции, функциональное уравнение 68—69
Томсона принцип в электростатике 253
Тон, высота тона 268
Трансверсальность 201—205
Угловые точки, условие Вейерштрасса — Эрдманна для угловых точек 245
Узловые линии 284 286 287 372
Узловые точки 284 429 442
Унитарная матрица 9
Унитарное преобразование 14
Условия разрыва 332 334 335 340 341 381
Фаза 268
Фейер, теорема Фейера о суммировании 94—95
Ферма, принцип Ферма 153
Фишер-Рисса теорема 102
Форма билинейная 10
Форма интегральная 113
Форма квадратичная 11
Формы, зависящие от бесконечно большого числа переменных 35
Фредгольм, теоремы Фредгольма 107 109
Фредгольм, формулы Фредгольма 132—135
Фридрихса преобразование 225 226
Фундаментальная лемма вариационного исчислений 174
Фундаментальные функции см. «Собственные функции»
Функционал 155
Функциональное пространство 51
Функциональное уравнение тета-функции 68—69
Функциональный аргумент 156
Фурье, интеграл Фурье 70—76
Фурье, коэффициенты Фурье 44 63
Фурье, коэффициенты Фурье порядок их малости 67
Фурье, ряд Фурье 62—70
Характеристические числа 19 23
Центр тяжести, теорема о движении центра тяжести 251
Цепная линия 160 210
Цилиндрические функции см. «Бесселевы функции» «Ганкеля «Матье функции «Неймана
Чебышева дифференциальное уравнение, применение метода интегрального преобразования 483—484
Чебышева полиномы 81 82—83 309—310 483 485
Число измерений последовательности функций 56 136 137 138
Шаровые функции Лапласа 297 298—299 485—496
Шаровые функции Лежандра 307—309 350 477—481
Шаровые функции Лежандра второго рода 480—481
Шаровые функции Лежандра высшего порядка 309 481
Шаровые функции Лежандра интегральные выражения 477—483
Шаровые функции Лежандра сопряженные 309 481
Шаровые функции Лежандра, асимптотические формулы 507—508
Шаровые функции Лежандра, дифференциальное уравнение 79—80
Шаровые функции Лежандра, как частный случай шаровых функций Лапласа 300
Шаровые функции Лежандра, производящая функция 79 483
Шаровые функции Лежандра, рекуррентные формулы 479
Шаровые функции обобщенные 300
Шаровые функции симметрические 487
Шаровые функции, выражение Максвелла — Сильвестра 489—496
Шаровые функции, полнота системы шаровых функций Лапласа 487
Шаровые функции, теорема о разложении 488
Шварц, неравенство Шварца для векторов 2
Шварц, неравенство Шварца для функций 42
Шестигранник, софокусный ортогональный 301
Шлефли, интегральное выражение шаровых функций Лежандра 477—479
Шмидт, метод вывода теорем Фредгольма 143—144
Шредингер, задача Шредингера о собственных значениях 322—324
Шредингер, задачи о собственных значениях шредингеровского типа 423
Штейнера задача 154
Штейнера задача, решение изопериметрической задачи 162—163
Штурм — Лиувилля задача о собственных значениях 275—278 306—312 312——320 379 432
Эйлер, дифференциальное уравнение Эйлера 175
Эйлер, преобразование Эйлера 445
Экстремали 175 178
Экстремали ломаные 245
Элементарный делитель 39
Эллиптические координаты 217
Эллиптические координаты вырождающиеся 220—221
Эллиптические функции 218 219
Энергия, интеграл энергии 253
Энског 144
Эрдман, условие для угловых точек 245
Эрмита дифференциальное уравнение, применение метода интегрального преобразования 484
Эрмита ортогональные функции 351
Эрмита полиномы 310 484
Эрмита полиномы, их производящая функция 485
Ядро выродившееся 106
Ядро итерированное 127
Ядро несимметрическое 145 147
Ядро определенное 114
Ядро разрешающее или взаимное 130 135
Ядро симметрическое 113—124
Ядро, допускающее симметризацию 150
Ядро, определение 104
Якоби, полиномы Якоби 81 83 309—310
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



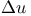 к полярным координатам
к полярным координатам