|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Grimmett G. — Percolation |
|
|
 |
| Предметный указатель |
Isoperimetric inequality 284
Jacobs, D.J. 75 366
Jikov, V.V. 381—382
k-dependence 178 196
Kagome lattice 54
Kalai, G. 52
Kalikow, S. 355—356
Kantor, T. 75 364
Kapitulnik, A. 253
Kasteleyn, P.W. 8 34 51 115 394
Keane, M. ix 51 198 204 229—230 239 345 348 354—357
Kesten, H. ix—x 17 29—30 37—38 51 55 75—76 81 84—86 114—115 118 142—145 196 206 214 222 229—231 247—253 278—281 286—288 297 315 324—329 338 345—351 355 361 365—371 374 380—382
Kiinnemann, R. 381
Klein, S.T. 230
Klein, W. 249
Kolmogorov, A.N. 260
Kong, X.P. 383
Koplick, J. 367
Kotecky, R. 396
Kozlov, S.M. 381—382
Kunz, H. 139 145 222 231
Kuulasmaa, K. 393
Laanait, L. 396
Lace expansion 56 233 270 275 280
Langlands, R.P. 253 347
Large deviations 81 196 231 348 371
Large deviations for animals 81
Lattice 9
Lattice, definition 349
Lattice, dual pair 53 283
Lattice, line 24
Lattice, matching pair 345
Left-right crossing 50 179 226 294 295 315 346 388
Leftmost vertex 207
Lenormand, R. 367
Lerman, K. 367
Levin, D. 231
Licea, C. 371
Lieb, E.H. 115 144
Liggett, T.M. 193 196 230 368—370 393
Line graph, lattice 24
Local change 61
Loffler, A. 86
Long-range percolation 3 29 115
Long-range percolation in one dimension 351
Long-range percolation on half-space 355
Lorentz model 383
Lorentz, H. 382—383
Lowest 317
Luczak, T. 351
Lyons, R. 29 350 390
Madras, N. 30
Magnetic field 7 102 105
magnetization 23
Malyshev, V.A. 310
Mandelbrot, B. 386
Marstrand, J.M. 147—149 155 196 354 357
Martingale, convergence theorem 36
Martingale, method 311 312
Matching lattices 55 345
Mauldin, R.D. 387
Max-flow min-cut theorem 50 378
Maximum flow 378
McDiarmid, C.J.H. 51 350
McKay, B. 29 349
McLeish, D.L. 311
Mean cluster size 20 23 87 132 232
Mean cluster size, analyticity 142
Mean cluster size, differentiability 224
Mean cluster size, power law in two dimensions 325
Mean field theory 255 263 269
Mean size of finite cluster 23
Mean size of finite cluster, differentiability 224
Mean size of finite cluster, power law in two dimensions 325
Meester, R. 374 386—389
Meiron, D. 75 367
Menger's Theorem 91
Menshikov, M.V. ix 29—30 75 88—89 115 253 278 348 373 385
Messager, A. 396
Method of moments 310 312
Miracle-Sole, S. 396
Mirror 382
Mixed percolation 29 350
Modica, L. 381
Molchanov, S.A. 29—30 88 115 373
Moore, E.F. 46 51
Morton, W. vii
Mossel, E. 231
Motion 364
Murty, U.S.R. 285 345
Neaderhouser, C.C. 311
Newman, C.M. x 22 29 75 86 115 130 133 144—147 163 170 174 196 210 229—231 252 263 268—271 278—279 311 325 347 350 353—357 369—371 396
Ney, P.E. 278
Nguyen, B.G. 86 278—279
Nienhuis, B. 279
Nijs, M.P.M. den 279
Ninham, B.W. 382
North-east lattice 367
Number of clusters per vertex 20 23 77 116 232 248 285 309
Number of clusters per vertex, analyticity 142 145 285
Number of clusters per vertex, central limit theorem 311
Number of clusters per vertex, differentiability 84 145 224 279 285 325
Oleinik, O.A. 381—382
Open cluster 11
Open cluster, largest 145
Open cluster, sequential construction 28 154 171 211
Open edge 10
Open path 11
Open path, longest 145
Oriented percolation 29 367
Oriented percolation in high dimensions 369
Origin 10 24 55 283
Ornstein — Zernike decay 127 145
Ornstein, L.S. 127 145
Orzechowski, M.E. 386
p-open edge 11 152 204 367
Papanicolaou, G. 381
Parallel law 394
Partial order 11
Partition 200
Partition function 116
Partition, compatible 200
Passage time 370
Path 11
Path, closed 11
Path, open 11
Path, self-avoiding 15 30
Path, self-repelling 66
Pearson, R.P. 279
Peierls argument 16 222
Peierls, R. 16 222
Pemantle, R. 230—231 390
Penrose, M. 196
Percolation 9
Percolation in half-spaces 162
Percolation in high dimensions 269
Percolation in slabs 147
Percolation in three dimensions 359
Percolation in three dimensions, area law 361
Percolation in three dimensions, duality 360
Percolation in three dimensions, perimeter law 361
Percolation in three dimensions, surfaces 359
Percolation in two dimensions 281
Percolation in two dimensions on subsets 303
Percolation in two dimensions, central limit theorems 309 311
Percolation in two dimensions, cluster size distribution 296
Percolation in two dimensions, continuity of  288 288
Percolation in two dimensions, correlation length 304
Percolation in two dimensions, critical exponents 252 279
Percolation in two dimensions, critical probability equals 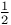 87 114 285 287 87 114 285 287
| Percolation in two dimensions, duality 283
Percolation in two dimensions, existence of open circuits 288
Percolation in two dimensions, number of clusters per vertex 285 309
Percolation in two dimensions, number of clusters per vertex, analyticity 285 325
Percolation in two dimensions, number of clusters per vertex, differentiability 279 285 325
Percolation in two dimensions, open circuits in annuli 314 316
Percolation in two dimensions, percolation probability 279
Percolation in two dimensions, percolation probability, non-differentiability 43 279
Percolation in two dimensions, power laws 324
Percolation in two dimensions, supercritical phase 295
Percolation in two dimensions, truncated connectivity function 295
Percolation in two dimensions, wedges 305
Percolation on trees 230 238 254 350
Percolation probability 13 23 24 232
Percolation probability for continuum percolation 373
Percolation probability for oriented percolation 368
Percolation probability, continuity 202
Percolation probability, critical exponent 233 270
Percolation probability, differentiability 224
Percolation probability, non-differentiability in two dimensions 43 279
Percolation probability, power law in two dimensions 325
Percolation, continuum 86 371
Percolation, dual process 281 284
Percolation, first-passage 29 369
Percolation, fractal 383 389
Percolation, high density 29
Percolation, inhomogeneous 3 29 331 350
Percolation, invasion 366
Percolation, long-range 3 29 115 351
Percolation, mixed 3 29 349 350
Percolation, oriented 29 367
Percolation, probability 12 23 24 232
Percolation, randomly oriented 369
Percolation, spread out 86 275 280 352
Peres, Y. 29 230—231 350 389—390
Periodic graph 349
Pernod 2
Peyriere, J. 387
Phase transition 253
Pichet, C. 347
Pin-ball 382
Pisztora, A. 196 231
Pivotal edge 42
Piza, M.S.T. 371 396
Planar duality 53 282 283 345
plaquette 360
Plaquette surface 359
Plaquette surface, boundary 360
Point at infinity 103
Poisson blob model 371
Poisson process 371
Pokorny, M. 75 367
Polymerization 374
Porous stone 1 313
positive correlation 34
Positive definite 270
Potts model 76 394
Potts, R.B. 76 394—396
Pouliot, P. 253 347
Power law 232 324
Power law in high dimensions 270 280
Power law, inequalities 324
Probability space 10
Proschan, F. 46 51
RADIUS 88 118 120 197 235
Radius, exponential decay 88 117 205
Radius, power law in two dimensions 324
Random walk 231 251
Random, electrical network 6 380
Random, electrical network, on complete graph 382
Random, electrical network, on tree 382
Random, medium 1
Random-cluster model 52 76 196 393
Random-walk point 384
RANGE 352
Rate of cure 391
Rate of infection 391
Redner, S. 249
Reed, M. 271
Reimer's inequality 39
Reimer, D. 38—39 51
Reliability theory 46
Renewal process 91
Renormalization 146 233 244 253
Renormalization, dynamic 147
Renormalization, static 147 176 196
Resistance 6
Reynolds, P.J. 249
Richardson, D. 370
Riedel, E.K. 279
Rightmost vertex 208
Rigid 365
Rigidity percolation 75 364
Rigidity percolation, component 366
Rigidity percolation, critical probability 365
Rigidity percolation, probability 365
Riischendorf, L. 51
Rogers, C.A. 349
Root 254
Rotator model 384
Roy, R. 374
RSW theorem 288 315 348
Rudin, W. 271
Ruelle, D. 352
Ruijgrok, T.W. 384
Ruiz, J. 396
runs 30
Russo's formula 33 43 46
Russo, L. viii xi 30 33 41—46 50—52 61 90 102 105—106 109 114—115 196 203 224 229—231 263—265 271 281 287—288 291 314—317 322 345—348 360—361
Saint-Aubin, Y. 253 347
Scaling hypothesis for cluster size 239
Scaling hypothesis for connectivity function 240
Scaling relations 235 241 252 279
Scaling theory 232 233 239 252
Scheinerman, E.R. 351
Schick, M. 279
Schinazi, R.B. 8 393
Schonmann, R.H. ix 30 193 196 206 214 230 297 347 350 369
Schramm, O. 29 253 350
Schulman, L.S. 229—231 354—356
Schwartz, J.T. 78 228
Seed 149 150 163
Self-avoiding path, walk 15 30
Self-duality 16 283
Self-matching lattice 55
Self-repelling path 66
Semiconductors 367
Series expansion for 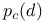 75 280 75 280
Series law 394
Servatius, B. 365
Servatius, H. 365
Sevsek, F. 351
Seymour, P.D. 30 114—115 281 287—288 291 314—315 345 348
Shamir, E. 230
Shannon, C.E. 46 51
Shape theorem 370 392
Shlosman, S. 396
Side stacking 172
Sidorenko, A.F. 29—30 88 115 373
Sierpinski carpet 389
Simon — Lieb inequality 144
Simon, B. 144 271
Simultaneous uniqueness 229
Sinai, Ya. G. 383
Sink vertex 378
Site percolation 24 66 71 350
Site-box 155
Skeleton 135
Slab 66 146 196
Slab, critical probability of s. 146 148 361
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте