|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Dorfman I. Ч Dirac Structures and Integrability of Nonlinear Evolution Equations |
|
|
 |
| ѕредметный указатель |
 -scheme for the KdV, Benjamin Ч Ono and Kadomtsev Ч Petviashvili equations 151Ч154 -scheme for the KdV, Benjamin Ч Ono and Kadomtsev Ч Petviashvili equations 151Ч154
 -scheme in Hamiltonian framework, symmetries of Dirac structures 154Ч157 -scheme in Hamiltonian framework, symmetries of Dirac structures 154Ч157
 -scheme of integrability 148Ч165 -scheme of integrability 148Ч165
 -scheme of integrability, examples with conserved Dirac structures 157Ч159 -scheme of integrability, examples with conserved Dirac structures 157Ч159
 -scheme, Hamiltonian pairs 159Ч160 -scheme, Hamiltonian pairs 159Ч160
 -scheme, Lenard scheme 161Ч165 -scheme, Lenard scheme 161Ч165
 -scheme, Lie derivatives in constructing 167 -scheme, Lie derivatives in constructing 167
 -scheme, Liouville equation 164Ч165 -scheme, Liouville equation 164Ч165
 -scheme, sine-Gordon equation 163Ч164 -scheme, sine-Gordon equation 163Ч164
2-cococycles 35 98Ч99
3-dihedral group of algebraic structures 137Ч139
Adler Ч Gelfand Ч Dikii method 106Ч111 113Ч114
Algebraic theory, Dirac structures 8Ч32
Belavin Ч Drinfeld solutions, Yang Ч Baxter equation 29Ч32
Benjamin Ч Ono (BO) equation 153 157
BenneyТs moment equations 102Ч104
Brackets see УPoisson bracketsФ УSchouten
Characteristic foliation 19Ч20
Coboundary 10 14 33Ч35
Cochains 10
Cocycles 10
Cohomologies 10 12 14 65Ч68 99
Commutative symmetry algebra 148Ч154
Complex of formal variational calculus 57Ч74
Complex of formal variational calculus, cohomology group 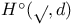 65Ч68 65Ч68
Complex of formal variational calculus, construction 57Ч60
Complex of formal variational calculus, exactness problem 62Ч65
Complex of formal variational calculus, general procedure of solving 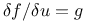 69Ч73 69Ч73
Complex of formal variational calculus, invariant operations expressed in terms of Frechet derivatives 61Ч62
Complex of formal variational calculus, the equation 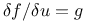 in the ring of polynomials and smooth functions 68Ч69 in the ring of polynomials and smooth functions 68Ч69
Complexes, de Rham 8 12Ч14 18Ч19 22 57Ч60
Complexes, over Lie algebra 11Ч15
Condition for operator to be Hamiltonian 77Ч79
Conjugate operator 14Ч15
Coupled nonlinear wave equation (CNW) 89Ч97
de Rham complex 8
de Rham complex of a ring 12Ч14
de Rham complex, construction 57Ч60
de Rham complex, Dirac structures 18Ч19
de Rham complex, symplectic operators 22
Density of the functional 59
Differential-geometric type symplectic operators of 146Ч147
Dirac structures,  -scheme 154Ч159 -scheme 154Ч159
Dirac structures, algebraic theory 8Ч32
Dirac structures, basic to Hamiltonian theory 4
Dirac structures, constituting a pair 127Ч130
Dirac structures, definition 16Ч17
Dirac structures, finite-dimensional class 18Ч19
Dirac structures, Hamiltonian operators 22Ч27
Dirac structures, Lenard scheme of integrability 48Ч51
Dirac structures, Nijenhuis relations 45Ч51
Dirac structures, Nijenhuis relations; pairs of Dirac structures 45Ч51
Dirac structures, pairs of, and Nijenhuis operators 33Ч56
Dirac structures, reduction to symplectic structures 5Ч6
Dirac structures, related to Liouville, sine-Gordon, modified KdV and nonlinear Schrodinger equations 131Ч136
Dirac structures, symplectic operators 20Ч22
Dubrovin Ч Novikov-type Hamiltonian structures 104Ч106
Evolution equations, integrability 34 6Ч7
Evolution equations, related to local Hamiltonian operators 75Ч114
Evolution equations, related to local symplectic operators 115Ч147
Exactness problem in the complex of formal variational calculus 62Ч65
FaddeevТs auxiliary conditions 5
Foliation, characteristic 19Ч20
Frechet derivatives, complex of formal variational calculus 60Ч62
Frechet derivatives, Hamiltonian conditions 77Ч79
Frechet derivatives, local symplectic operators 116Ч119
Frobenius theorem 19Ч20 31
Functional, density of the 59
Graded spaces 8Ч10
Hamiltonian operators,  -scheme 154Ч157 -scheme 154Ч157
Hamiltonian operators, Adler Ч Gelfand Ч Dikii method of constructing, pairs 106Ч111 113Ч114
Hamiltonian operators, conditions in an explicit form 77Ч79
Hamiltonian operators, Dirac structure 22Ч27
Hamiltonian operators, Dubrovin Ч Novikov-type 104Ч106
Hamiltonian operators, first order, in the one-variable case 80Ч82
Hamiltonian operators, Kirillov Ч Kostant-type hydrodynamic structures 102Ч104
Hamiltonian operators, Korteweg Ч de Vries and Harry Dym equations 85Ч89
Hamiltonian operators, Lenard scheme for Hamiltonian and symplectic pairs 51Ч56
Hamiltonian operators, Lie derivatives in constructing Hamiltonian pairs 159Ч160
Hamiltonian operators, local, and evolution equations 75Ч114
Hamiltonian operators, pairs and associated Nijenhuis operators 42Ч48
Hamiltonian operators, third-order 82Ч85
Hamiltonian operators, upper bounds for the level of symplectic operators and 142Ч146
Hamiltonian operators, Virasoro algebra 100Ч102
Hamiltonian operators, Yang Ч Baxter equation 29Ч31
Hamiltonian theory, general algebraic scheme 8Ч32
Hamiltonian theory, introduction 1Ч7
Hamiltonian vector fields,  -scheme 154Ч157 -scheme 154Ч157
Hamiltonian vector fields, Dirac structures 17
Hamiltonian vector fields, symplectic operators 21Ч22
Harry Dym(HD) equations 85Ч89
Hereditary or A-operators 56
Homotypy, algebraic 63Ч64
Integrability, x-scheme 148Ч165 (see also УParticular subjectsФ)
| Invariant operations expressed in terms of Frechet derivatives 61Ч62
Invariants and symmetries 15Ч16
Inverse scattering method 34
Kadomtsev Ч Petviashvili(KP) equation 153Ч154 158
KdV (Korteweg-de Vries) equation,  -scheme 151Ч153 158Ч159 162Ч163 -scheme 151Ч153 158Ч159 162Ч163
KdV (Korteweg-de Vries) equation, coupled nonlinear wave equation 89Ч97
KdV (Korteweg-de Vries) equation, Dirac structures 135
KdV (Korteweg-de Vries) equation, Hamiltonian dynamical system 5Ч6
KdV (Korteweg-de Vries) equation, Hamiltonian theory 3Ч7
KdV (Korteweg-de Vries) equation, Lenard schemes for the potential 125Ч130
KdV (Korteweg-de Vries) equation, local Hamiltonian operators 85Ч89
KdV (Korteweg-de Vries) equation, Virasoro algebra and two Hamiltonian structures of the 100Ч102
Kirillov Ч Kostant structures, Adler Ч Gelfand Ч Dikii method 106Ч111 113
Kirillov Ч Kostant structures, canonical example of a Poisson structure 4
Kirillov Ч Kostant structures, deformations of 96Ч100 113
Kirillov Ч Kostant structures, hydrodynamic, BenneyТs moment equations 102Ч104
Kirillov Ч Kostant structures, infinite-dimensional 89Ч97
Kirillov Ч Kostant structures, symplectic structure 24
Kirillov Ч Kostant structures, Virasoro algebra 100Ч102
KN equation see УKrichever Ч Novikov(KN) equationФ
Korteweg-de Vries equation see УKdV (Korteweg-de Vries) equationФ
KP equation see УKadomtsev Ч Petriashvili(KP) equationФ
Krichever Ч Novikov(KN) equation, Hamiltonian presentation 6
Krichever Ч Novikov(KN) equation, Lenard scheme 122Ч125
Krichever Ч Novikov(KN) equation, pair of local symplectic operators 120Ч125 147
Lax type equations 109Ч111
Lenard scheme,  -scheme 161Ч165 -scheme 161Ч165
Lenard scheme, applied to the Krichever Ч Novikov(KN) equation 122Ч125
Lenard scheme, for Hamiltonian and symplectic pairs 51Ч56
Lenard scheme, hierarchy of the Liouville equation 134Ч135
Lenard scheme, integrability for Dirac structures 33 48Ч51
Lenard scheme, KdV (Korteweg-de Vries) equation 93Ч94
Lenard scheme, Liouville equation 165
Lenard scheme, local Hamiltonian operators 85Ч89
Lenard scheme, sine-Gordon equation 133Ч134 163Ч164
Lenard scheme, two, for the potential KdV equation 125Ч130
Lie algebra, commutative symmetry 148Ч154
Lie algebra, complexes over 11Ч15
Lie algebra, de Rham complex 8
Lie algebra, deformations of, and Nijennuis operators 33Ч35
Lie algebra, framework for Dirac structures 6
Lie algebra, graded spaces 9Ч10
Lie algebra, Lie derivatives 15Ч16 159Ч160
Lie algebra, local Hamiltonian operators 90Ч97
Lie algebra, Poisson bracket 2Ч3
Lie algebra, skew-symmetry 2Ч3
Lie algebra, structures in the space of 1-forms 25Ч27
Lie algebra, Yang Ч Baxter equation 29Ч32
Liouville equation 3 41 134Ч135 164Ч165
Matrix differential operators, local Hamiltonian operators 75Ч77
Matrix differential operators, symplecticity conditions 115Ч117
Matrix differential operators, theorem 101Ч102
Nijennuis operators, deformations of Lie algebras 33Ч35
Nijennuis operators, Hamiltonian pairs 42Ч48
Nijennuis operators, hierarchies of 2-forms generated by regular structures 39Ч42
Nijennuis operators, Nijenhuis torsion, conjugate to 37Ч39
Nijennuis operators, pairs of Dirac structures 33Ч56
Nijennuis operators, pairs of Dirac structures, Nijenhuis relations 45Ч51
Nijennuis operators, properties of and two Dirac structures 129Ч130
Nijennuis operators, properties of, symmetry generation 36Ч37
Nonlinear Schrodinger(NLS) equations 135Ч136
Poisson brackets, Lenard scheme of integrability 50 52
Poisson brackets, Lie algebra structure 2Ч3 17Ч18
Poisson brackets, presymplectic manifold 4Ч5
Poisson brackets, reference 114
Presymplectic manifold 4Ч5
Reduction procedure 15Ч16
references 166Ч172
Ring of polynomials, complex of formal variational calculus 65 68Ч69
Schouten bracket, the 27Ч29 90Ч92
Schrodinger (NLS) system, nonlinear 135Ч136
Sine-Gordon equation 133Ч134 163Ч164
Skew-symmetry, Hamiltonian operators 26Ч27
Skew-symmetry, Lie algebra 2Ч3
Skew-symmetry, local Hamiltonian operators 76Ч77
Skew-symmetry, local symmetric operators 116Ч120
Skew-symmetry, mapping 14
Soliton theory 3 114
Structure function 96Ч100
Superalgebra, Lie 9Ч10 28
Symmetries and invariants 15Ч16
Symmetry generation, properties of Nijenhuis operators 36Ч37
Symplectic manifold 1Ч2 4Ч5
Symplectic operators, conditions guaranteeing symplecticity of a pair 54Ч55
Symplectic operators, constituting a pair 48
Symplectic operators, differential-geometric type 146Ч147
Symplectic operators, graphs of linear operators 20Ч22
Symplectic operators, Lenard scheme for Hamiltonian and symplectic pairs 51Ч56
Symplectic operators, local, and evolution equations related to them 115Ч147
Symplectic operators, many-variable case with linear dependence on 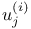 137Ч142 137Ч142
Symplectic operators, one-variable case: first- and third-order 117Ч120
Symplectic operators, upper bounds for the level of, and Hamiltonian operators 142Ч146
Virasoro algebra 100Ч102
Yang Ч Baxter equation, Belavin Ч Drinfeld solutions 29Ч32
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 -scheme for the KdV, Benjamin Ч Ono and Kadomtsev Ч Petviashvili equations
-scheme for the KdV, Benjamin Ч Ono and Kadomtsev Ч Petviashvili equations