|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Александров П.С., Маркушевич А.И., Хинчин А.Я. — Энциклопедия элементарной математики. Том I. Арифметика |
|
|
 |
| Предметный указатель |
Натуральные числа, монотонность сложения и умножения 143
Натуральные числа, порядок 96 135 142—145
Натуральные числа, система аксиом 133 152—156
Натуральные числа, сложение 135—138 148
Натуральные числа, умножение 139—142 148 149
Натуральный ряд 16 18 26 27
Натуральный ряд, мультипликативная база 202
Нейгебауер 41—43
Неопределённый (диофантов) анализ 284
Непер 70
Непера палочки 365—367
Непрерывная дробь см. «Цепная дробь»
Непрерывность функции 214 216 217
Нессельман 67
Низшая граница абсолютной погрешности 380
Номография 430
Нулевые последовательности 209
Нуль 39 40 49 51 54
Нуль кольца 110 111
Область целостности 111 169
Образ элемента 86
Обратная операция 101
Обратный элемент 105 115
Общее кратное двух чисел 261
Объединение множеств 82 83
Однер, В.Т. 367
Одо Клюнийский 59
Округление десятичных дробей 322
Округление результатов действий над приближёнными числами 400 401—405 413—417 420
Округление чисел по избытку 379
Округление чисел по недостатку 379
Округление чисел, правило чётной цифры 379
Операции над множествами 82
Относительная погрешность, граница 381
Отношение отрезков 189 190 196—198
Отображение множеств 85
Отрезок 82
Отрезок натурального ряда 89
Оценка результата приближённая («прикидка») 361
Палочки Непера 365—367
Пары чисел 159 163 164 166 174—177 179 231 232
Паскаль 12
Пеано 133
Пересечение множеств 82 83
Перфорационные карты 375
Планиметры 374
Погрешностей распределение 411—413
Погрешность см. «Абсолютная погрешность»
Погрешность большая (близкая к предельной) 411
Погрешность истинная и, граница погрешности 403
Погрешность округления 322 379
Погрешность относительная, граница 381
Погрешность предельная 400 410
Погрешность систематическая 384
Погрешность случайная 384
Погрешность средняя квадратическая 408 410
Подгруппа 108
Подкольцо 112 113
Подмножество 81 91
Подмножество собственное 81
Подполе 118 119
Подходящие дроби 301—304
Подходящие дроби, приближение чисел 323—328
Подходящие дроби, теоремы 328—334
Позиционный принцип счисления 11 35 50
Поле 113
Поле архимедовски расположенное 181 182 205
Поле действительных чисел 202 223
Поле действительных чисел, расположение и отображение 221
Поле комплексных чисел 228 230
Поле минимальное 160 161 173
Поле непрерывное 201
Поле полное 198
Поле простое 119
Поле расположенное 125—128
Поле рациональных комплексных чисел 114
Поле рациональных чисел 173—184
Поле характеристики 0 182 183
Поле характеристики p>0, пример 117
Поле, примеры 114
Полуинтервал 82
Полулогарифмическая бумага 430
Последовательности стационарные 211
Последовательность элементов множества 191
Последовательность элементов поля ограниченная 192
Последовательность элементов поля расходящаяся 192
Последовательность элементов поля сходящаяся 192—194
Правила подсчёта цифр 400 401—405 413—417 420
Предел последовательности элементов поля 192—195
Предельный элемент множества 225
Приближённое равенство 380
Приближённое равенство, точность 385
Приближённые значения 377
Приближённые значения, округление результатов 378
Приближённые формулы для вычислений 421 422 423
Приближённые числа, возведение в квадрат, куб 404
Приближённые числа, вычисление посредством логарифмов 420
Приближённые числа, извлечение квадратного и кубического корней 404
Приближённые числа, округление более точных данных 414
Приближённые числа, произведение 401—403
Приближённые числа, промежуточные результаты действий 414
Приближённые числа, сложение и вычитание 400 401
Приближённые числа, точность 381—383
Приближённые числа, умножение и деление 403 404
Приближённые числа, цифры, заслуживающие доверия (точные) 381
Приближённые числа, число цифр в данных 417
Приближённый результат 383
Принцип А.Н. Крылова 407—409
Принцип счисления аддитивный 31 48 73
Принцип счисления мультипликативный 31 36 15 47 48
Принцип счисления субтрактивный (вычитания) 29
Прообраз элемента 86
Прообраз элементаполный 86
Простые числа 256 262
Простые числа, распределение 263 266 267
Прошко, В.М. 376
Птолемей 67
Равенство множеств 81
Равномощность множеств 86 87
Равноостаточность чисел 273
Равноточвые измерения (способ обработки результатов) 386
Радианная мера угла 216
Разность множеств 82
Расширения принцип 157—159
Рациональные числа 172 173 179 180 186—188 299
Рациональные числа, единственность представления ценной дробью 299 300
Рациональные числа, представление систематической периодической дробью 312—314
Риман 269
Сакробоско (Галифакс) 53 55
Сечение упорядоченного множества 225
Система аксиом, независимость 155 156
Система аксиом, непротиворечивость 153
Система аксиом, полнота 153 154
Система вычетов по модулю полная 277 278
Система вычетов по модулю приведённая 278 279
Система счисления алфавитная 31—37 73
Система счисления аттическая (геродианова) 29 33
Система счисления в России 55 57
Система счисления вавилонская 39 40 42 43
Система счисления греческая 33
Система счисления двадцатиричная 13 22 31
Система счисления двенадцатиричная 12
Система счисления двоичная 17 29
Система счисления десятичная 11 12 22 73
Система счисления египетская 27—29 31 32 39
Система счисления индусская 44—46 48 49 50
Система счисления ионийская 33 36 37
Система счисления китайская 31
| Система счисления позиционная 12 13 32 36 38—50 53 54
Система счисления пятиричная 13 14 22
Система счисления римская 14 26 29 31 33 37
Система счисления славянская 33 37 38
Система счисления троичная 17
Система счисления шестидесятиричная 38 39 40 43
Систематическая (A-ичная) дробь 308
Систематическая дробь бесконечная 309
Систематическая дробь конечная 309 314
Систематическая дробь периодическая 312
Систематическая дробь смешанно-периодическая 312
Систематическая дробь чисто периодическая 312
Систематические дроби, их преимущества 306
Систематические дроби, представление чисел 309—314 316
Системы 83
Сокращённые приёмы вычислений 422—426
Сокращённые способы арифметических действий 439
Спасский, И.Г. 57
Способ границ 378 388
Способ границ погрешностей 392—399
Способ границ погрешностей, примеры применения теорем о границах погрешностей 395
Сравнений-метод 271—290
Сравнения алгебраические высших степеней 283 286—290
Сравнения линейные с одним неизвестным 283—286
Сравнения содержащие неизвестные 282
Сравнения тождественные 282 283
Сравнения, сложение, вычитание, умножение, деление, степень 273—276
Сравнимость 273
Срединное значение («медиана») 385
Среднее арифметическое значение 384
Среднее квадратическое отклонение 386
Среднее отклонение 385
Средняя квадратическая погрешность 408 410
Сталин, И.В. 73 74
Стевин, С. 69 70
Структурные константы (постоянные умножения) алгебры 243
Счёт 16—19 22—25 27 35 357
Счёт письменный 361 363
Счёт полуписьменный 359
Счёт устный 359 438
Счётная линейка, логарифмическая шкала 434
Счётная логарифмическая линейка 431
Счётная метрическая линейка 432 433
Счётно-анатитические машины 374 376
Счётно-решающие устройства 374
Счётно-решающие устройства непрерывного действия 374
Счётно-решающие устройства, моделирование 374
Счёты русские 365 366
Таблица разностей 375 376
Табулятор 376
Таннери 33 35
Тейлор 16
Тело 241
Тело кватернионов 244
Тело кватернионов рациональных 251
Теорема Евклида о бесконечности множества простых чисел 262 297
Теорема Лиувилля 344
Теорема о законности индуктивных доказательств 134
Теорема о последовательных подходящих дробях 331
Теорема о промежуточном значении 218—220
Теорема основная делимости чисел 257—262
Теорема Ферма («малая») 280
Теорема Фробениуса 249
Теорема Чебышева 340
Теоремы Дирихле 269 336—338
Теоремы Лежандра 328 330
Теоремы Эйлера 264 279
Теория чисел, методы см. «Методы теории чисел»
Тимченко, И.Ю. 47
Тип множества 97
Толстов, С.П. 52
Точность (потеря точности при вычитании) 418
Точность приближённого числа 381 382
Точность результата логарифмических вычислений 418 419
Точные цифры 382
Трансцендентные числа 343
Трансцендентные числа Лиувилля 343 345
Трансцендентные числа, построение их 343—347 349
Тюро-Данжен 43
Ферма 289
Ферма теорема («малая») 280
Финэ 69
Фробениуса теорема 249
Фундаментальная последовательность элементов поля (последовательность Коши) 196
Функции непрерывные, примеры 216—218
Функции тригонометрические, определение 216 217
Функция 84
Функция 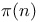 263 268 263 268
Функция 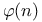 268 269 280—282 268 269 280—282
Функция действительного переменного 214
Функция дробная рациональная 216
Функция заданная на множестве 85 146
Функция непрерывная в точке 214 216 218
Функция целая рациональная 216
Функция, область значений 85
Функция, область определения 85
Характеристика поля 116 117
Характеристика поля расположенного 128
Хисс 35
Целые числа 15 16 57 170 171
Целые числа алгебраические, разложение 257
Целые числа, классы по модулю 277
Цепные дроби 298 299 305 307
Цепные дроби бесконечные 315—321
Цепные дроби, представление чисел 321
Цифры 50 51 54 308
Цифры арабо-индусские 52
Цифры индусские 53 55
Цифры римские 52 53
Цифры славянские 55 57
Цифры «губар» 50—52
Чебышев, П.Л. 255 268 269 339 372
Чебышева арифмометр 372
Чебышева теорема 340
Черепнин, Л.В. 60
Числа 157 158
Числа e и  350 351 350 351
Числа алгебраические 343
Числа алгорифмические 13 14 24 25 27
Числа действительные 188 202
Числа дробные 172 180
Числа иррациональные 188 214
Числа количественные 140
Числа комплексные 227 228
Числа натуральные 11 22 73 133 262
Числа порядковые 140
Числа простые 256 262
Числа рациональные 172 173 179 180 186 187 188
Числа совокупности 23 24 47 48
Числа составные 256
Числа сравнимые по модулю 273
Числа трансцендентные 343
Числа узловые 13 14 24 25 27 45 73
Числа, понятие числа 15 16 18 21 77 78
Числовая система йорубов 25
Числовое поле Гаусса 251
Числовой ряд 24 25 26 27
Числовые знаки разных народов 28 30
Числовые области, конструктивное определение 223
Числовые обозначения ацтеков 25 31
Шнирельман, Л.Г. 270
Шюке 38
Эйлер, Л. 255 263 279
Эйлера теоремы 264 279
Эквивалентность последовательностей 207 208
Эквивалентные пары 175—177
Элемент множества 80
Энгельс, Ф. 16 17 77 121
Янжул, И.Н. 376
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте