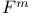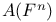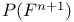|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Gruenberg K.W., Weir A.J. — Linear Geometry |
|
|
 |
| Предметный указатель |
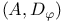 or or 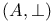 , generalized similarity euclidean geometry 131 132 , generalized similarity euclidean geometry 131 132
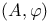 or A, generalized affine geometry 35 or A, generalized affine geometry 35
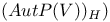 , automorphisms of , automorphisms of 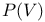 leaving H invariant 61 leaving H invariant 61
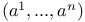 , dual basis of , dual basis of 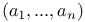 80 80
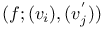 , matrix of f with respect to ordered bases , matrix of f with respect to ordered bases 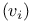 , , 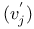 72 72
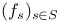 , family 2 , family 2
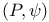 or P, generalized projective geometry 35 or P, generalized projective geometry 35
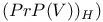 , collineations of , collineations of 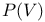 leaving H invariant 61 leaving H invariant 61
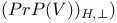 , collineations of , collineations of 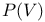 which restrict to collineations of which restrict to collineations of 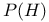 preserving preserving 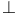 145 145
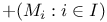 , , 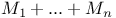 , sum 7 , sum 7
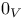 , zero element of V 5 , zero element of V 5
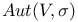 , orthogonal group on euclidean space , orthogonal group on euclidean space 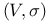 144 144
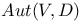 , automorphisms of V preserving D 144 , automorphisms of V preserving D 144
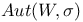 , unitary group on Hilbert space , unitary group on Hilbert space 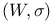 146 146
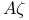 , matrix , matrix 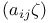 124 124
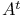 , transpose of A 77 , transpose of A 77
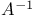 , inverse of A 73 , inverse of A 73
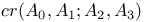 , cross-ratio 133 (ex. 1) , cross-ratio 133 (ex. 1)
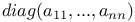 , diagonal matrix 104 , diagonal matrix 104
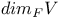 , dimension of V over F 10 , dimension of V over F 10
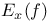 , eigenspace of f corresponding to eigenvalue x 135 , eigenspace of f corresponding to eigenvalue x 135
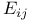 , matrix with (i,j)-term 1 and others 0 74 (ex. 2) , matrix with (i,j)-term 1 and others 0 74 (ex. 2)
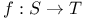 , mapping f of S into T 2 , mapping f of S into T 2
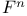 , n-tuples 5 , n-tuples 5
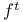 , transpose of f 83 (ex. 7) , transpose of f 83 (ex. 7)
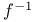 , the inverse of f 3 (ex. 1) , the inverse of f 3 (ex. 1)
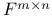 , , 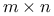 matrices 72 matrices 72
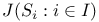 , , 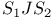 , join 16 , join 16
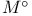 , annihilator of M 81 , annihilator of M 81
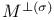 , , 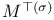 , subspaces orthogonal to M 93 , subspaces orthogonal to M 93
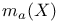 , minimum polynomial at a 151 , minimum polynomial at a 151
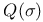 , quadric 111 , quadric 111
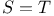 , S equals T 2 , S equals T 2
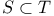 , S is contained in T 1 , S is contained in T 1
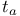 , translation , translation 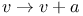 42 42
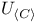 , complexification of real space U 14 , complexification of real space U 14
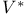 , dual space of V 80 , dual space of V 80
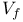 , F[X]-module defined by , F[X]-module defined by 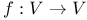 151 151
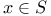 , x is an element of S 1 , x is an element of S 1
![$[S]_f$](/math_tex/7424b3f3da19d2094df1fab166b89e2582.gif) , submodule of , submodule of 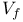 generated by S 153 generated by S 153
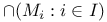 , , 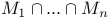 , intersection 3 , intersection 3
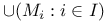 , , 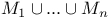 , union 3 , union 3
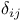 , Kronecker delta 73 , Kronecker delta 73
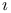 , canonical isomorphism , canonical isomorphism 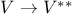 81 81
 , complex numbers 1 , complex numbers 1
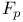 , integers modulo p 1 , integers modulo p 1
 , rational numbers 1 , rational numbers 1
 , real numbers 1 , real numbers 1
 , integers 1 , integers 1
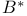 , dual proposition 84 , dual proposition 84
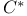 , dual configuration 84 , dual configuration 84
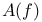 , mapping of affine geometries induced by , mapping of affine geometries induced by 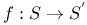 42 42
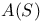 , affine geometry on coset S 16 , affine geometry on coset S 16
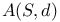 , euclidean geometry on coset S with distance d 127 , euclidean geometry on coset S with distance d 127
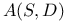 , similarity euclidean geometry on coset S with distance class D 131 , similarity euclidean geometry on coset S with distance class D 131
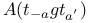 , affinity 42 , affinity 42
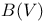 , bilinear forms on V 89 , bilinear forms on V 89
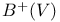 , symmetric bilinear forms on V 101 (ex. 4) , symmetric bilinear forms on V 101 (ex. 4)
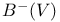 , skew-symmetric bilinear forms on V 101 (ex. 4) , skew-symmetric bilinear forms on V 101 (ex. 4)
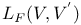 , linear mappings of V into , linear mappings of V into 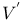 68 68
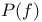 , mapping of projective geometries induced by , mapping of projective geometries induced by 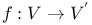 45 45
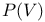 , projective geometry on vector space V 29 , projective geometry on vector space V 29
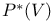 , dual geometry 86 , dual geometry 86
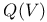 , quadratic forms on V 102 (ex. 9) , quadratic forms on V 102 (ex. 9)
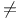 , is not equal to 2 , is not equal to 2
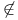 , is not an element of 2 , is not an element of 2
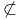 , is not contained in 2 , is not contained in 2
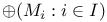 , , 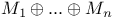 , direct sum 7 , direct sum 7
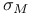 , restriction of , restriction of  to subspace M 95 to subspace M 95
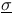 , , 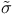 , linear mappings induced by the bilinear form , linear mappings induced by the bilinear form  91 91
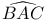 , angle 128 , angle 128
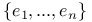 , standard basis of , standard basis of 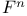 13 13
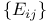 , standard basis of , standard basis of 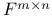 74 (ex. 2) 74 (ex. 2)
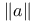 , norm of a 125 , norm of a 125
(d), class of distances similar to d 131
0, zero matrix 72
a(S), annihilator (ideal) of S 151
Af A, affine group on A 59
Affine geometry see "Geometry"
Affinity 42ff
Affinity, degenerate 70ff
angle 126 128
Annihilator 81
Annihilator, ideal 151
Annihilator, mapping 81 94
Anti-automorphism 120 122
Anti-isomorphism 84
Associative law for mapping multiplication 3 (ex. 3)
Associative law for matrix multiplication 73
Aut V, general linear group 59
Aut X, automorphisms on X; X = V, F, A or P 59
Automorphism groups for V, A, P, F 59
Automorphism of euclidean geometry 140ff
Automorphism of field 56 58 2) 65 123
Automorphism of Hilbert space 146
Automorphism of R-module 154
Automorphism of sesquilinear space 124
Automorphism of similarity euclidean geometry 144
Automorphism of vector space 66
Axis, of central collineation 48 (exx. 3—5)
Basis (base) 9ff
Basis cartesian 127 142 146
Basis dual 80
Basis of torsion-free F[X]-module 163
Basis standard, of ![$F[X]^n$](/math_tex/8c00c93bc7afc04ddad728c954a4c44b82.gif) 168 168
Basis standard, of 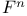 12 (ex. 9) 13 12 (ex. 9) 13
Basis standard, of 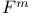 74 (ex. 2) 74 (ex. 2)
Bilinear form 89ff
Bilinear form, alternating 99
Bilinear form, degenerate 91 92
Bilinear form, negative definite 106
Bilinear form, orthosymmetric 97 101
Bilinear form, positive definite 10(1
Bilinear form, skew-symmetric 99 101 4)
Bilinear form, symmetric 97 101 4 8 9)
Bilinear polynomial 90
C(Q), representative cone of projective quadric Q 115
Canonical matrix rational 166
Canonical matrix, Jordan (classical) 167
Cartesian basis 127 142 146
Center of (central) collineation 48 (exx. 3—6) 54 63 83
Center of affine polarity 111 (ex. 5)
Center of affine quadric 119
Center of perspective of two triangles 23
Center of perspectivity 48 (ex. 6) 65
Center of sphere 133 (ex. 3)
Central collineation 48 (exx. 3—6) 54 62ff 83
Central collineation, center of see "Center"
Central collineation, hyperplane of 63
Centroid 48 (ex. 2)
Characteristic 2
Characteristic (Fano's Theorem) 40
Characteristic, field of 40 99ff
Classical (Jordan) canonical matrix 167
Classification of collineations 170ff
Coefficient space 50
Collineation 45 170ff
Collineation, central see "Central"
Completeness of Hilbert space 147
Completion of affine quadric (to projective quadric) 117 118 120
Complexification of real bilinear form 124 146
Complexification of real vector space 14 58 112 134 136 140
Cone, representative 115
Congruence of bilinear forms 89 90 103ff
Congruence of matrices 86 90 103ff
conic 111 114 120 2)
Conic section 116
Coordinate row (homogeneous) of a projective point 47
Coordinate row of a vector 13
Coordinate row of an affine point 44
| Coordinate system (homogeneous) for a projective geometry 46
Coordinate system for a euclidean geometry 129
Coordinate system for a vector space 13
Coordinate system for an affine geometry 44
Correlation 85 110 120
Correlation, degenerate 110
Coset (translated subspace) 15ff
Coset parallel 18
Coset, dimension of 16
Coset, space of 67 154
Coset, subspace belonging to 16
Cross-ratio 132 133 2 5 6)
d(a,b), distance from a to b 125
Degenerate, affine polarity 111 (ex. 6)
Degenerate, affine quadric 119
Degenerate, affinity 70
Degenerate, bilinear form 91 92
Degenerate, correlation 110
Degenerate, null-polarity 110
Degenerate, polarity 110
Degenerate, projective quadric 112
Degenerate, projectivity 70
Degenerate, subspace (with respect to a bilinear form) 92 (ex. 1) 95
Desargue's Theorem (affine) 23
Desargue's Theorem (projective) 32 (ex. 6) 38 41 48 51 86
Desargue's Theorem, converse of 38
Desargue's Theorem, related to a division ring 39 40 48
Determinant 144
Dilatation 44 (ex. 3) 49 54 63 75
Dimension of a coset 16
Dimension of a projective geometry 30
Dimension of a vector space 10ff
Dimension of an affine geometry 16
Dimension, finite 9ff
Dimension, projective 30
Direct sum of submodules 155ff
Direct sum of subspaces 7 8 8) 11 12 95 96 102ff 155ff
Distance on a coset 127
Distance on a euclidean space 125
Distance on a Hilbert space 146
Distance on a vector space 125
Distance, similar 131
Division ring 39 49 11) 75
Dual basis 80
Dual configuration 84
Dual frame of reference 87 88
Dual geometry 86ff
Dual space 80
Dual, proposition 84
Dual, self- 171 172
Duality 85
Duality, principle of 84
Eigenspace 71 (ex. 4) 135 142 143
Eigenvalue 71 (ex. 4) 135 137 141ff
Eigenvector 71 (ex. 4) 135ff 140 141ff
Elementary divisors of a finitely generated F[X]-module 159 160
Elementary divisors of a linear mapping 166
Elementary divisors of a matrix 168 169
Elementary move 164 165 2)
Elementary transformation 70 (ex. 10)
Embedding theorem 32 52 61 116 130
Equation linear 49ff 79ff 82
Equation of affine quadric 117ff
Equation of euclidean quadric 138ff
Equation of projective quadric 112ff
Equivalence of matrices 77 165
Exchange Lemma 9
Exponent of commutative group 153 (ex. 4)
Family 2
Fano's Theorem 40
Field 4 5
Field of characteristic 2 40 99ff 115)
Field of gaussian numbers 14 (ex. 1)
Field of quotients 160
Field, ground 12
Finite dimensional vector space 9ff
Finite field 109 (exx. 8—11) 162 174
Finite geometry (affine) 20 (ex. 1) 21) 38
Finite geometry (projective) 32 (exx. 4 5) 40 41 119 174
Form Hermitian 122ff
Form linear 80ff 101
Form quadratic 100ff
Form sesquilinear 121ff
Frame of reference for 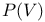 determined by a basis of V 46 determined by a basis of V 46
Frame of reference for a euclidian geometry 129
Frame of reference for a projective geometry 46
Frame of reference for an affine geometry 43
Frame of reference, standard, for 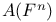 43 43
Frame of reference, standard, for 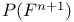 47 47
Function see "Mapping"
F[X], polynomials in X 6
Gaussian number field 14 (ex. 1)
Generator of a projective quadric 114 (exx. 11—14)
Geometry, "affine, of dimension n over F" 22
Geometry, "projective, of dimension n over F" 32
Geometry, affine 16ff 35
Geometry, affine, in 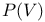 determined by H 36 61 130 determined by H 36 61 130
Geometry, Euclidean 127ff
Geometry, projective 29ff 35
Geometry, similarity euclidean 13Iff
Geometry, similarity euclidean, determined in 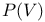 by H and D 132 by H and D 132
Greatest common divisor 161 (exx. 3 6)
Ground field 12ff
Group 4
Group, abelian (commutative) 4 150 160 163
Group, affine 59 75
Group, automorphism 59
Group, collineation (projective) 59
Group, commutative see "Group abelian"
Group, general linear 59
Group, homomorphism of 59
Group, isomorphism of 59
Group, orthogonal 144
Group, permutation 4 62
Group, projective see "Group collineation"
Group, rotation 4 144
Group, unitary 146
Harmonic conjugate, (affine) 27
Harmonic conjugate, (projective) 40
Harmonic constructive, (affine) 27
Harmonic constructive, (projective) 40 52
Harmonic range, (affine) 27
Harmonic range, (projective) 40 113 133
Hermitian form 122ff 124 3)
Hermitian mapping 147 (ex. 6)
Hermitian matrix 124 (ex. 2)
Hilbert space 146ff
Homogeneous (projective) coordinate row 47
Homogeneous linear equations 50
Homogeneous vector 22ff 30
Homomorphism of groups 59
Homomorphism of R-modules 154
Homomorphism of vector spaces 66
Hyperplane at infinity 36
Hyperplane in affine geometry 16
Hyperplane in projective geometry 30
Hyperplane of a central collineation 63ff
I, identity matrix 73
Ideal 152
Ideal, annihilator 151
Ideal, principal 152
Identity element of group 4
Identity element of ring 149
Identity mapping 2 3
Identity matrix 73
Image 2
Incidence propositions, (affine) 19
Incidence propositions, (projective) 31
Indecomposable submodule 159
Index notation 2
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



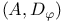 or
or 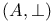 , generalized similarity euclidean geometry
, generalized similarity euclidean geometry 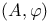 or A, generalized affine geometry
or A, generalized affine geometry 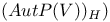 , automorphisms of
, automorphisms of 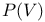 leaving H invariant
leaving H invariant 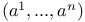 , dual basis of
, dual basis of 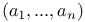
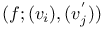 , matrix of f with respect to ordered bases
, matrix of f with respect to ordered bases 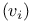 ,
, 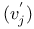
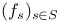 , family
, family 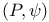 or P, generalized projective geometry
or P, generalized projective geometry 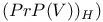 , collineations of
, collineations of 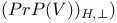 , collineations of
, collineations of 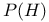 preserving
preserving 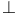
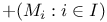 ,
, 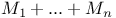 , sum
, sum 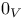 , zero element of V
, zero element of V 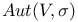 , orthogonal group on euclidean space
, orthogonal group on euclidean space 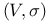
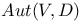 , automorphisms of V preserving D
, automorphisms of V preserving D 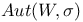 , unitary group on Hilbert space
, unitary group on Hilbert space 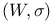
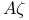 , matrix
, matrix 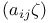
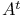 , transpose of A
, transpose of A 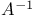 , inverse of A
, inverse of A 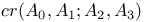 , cross-ratio
, cross-ratio 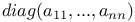 , diagonal matrix
, diagonal matrix 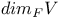 , dimension of V over F
, dimension of V over F 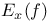 , eigenspace of f corresponding to eigenvalue x
, eigenspace of f corresponding to eigenvalue x 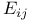 , matrix with (i,j)-term 1 and others 0
, matrix with (i,j)-term 1 and others 0 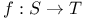 , mapping f of S into T
, mapping f of S into T 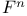 , n-tuples
, n-tuples 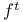 , transpose of f
, transpose of f 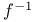 , the inverse of f
, the inverse of f 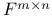 ,
, 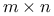 matrices
matrices 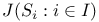 ,
, 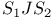 , join
, join 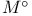 , annihilator of M
, annihilator of M 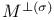 ,
, 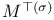 , subspaces orthogonal to M
, subspaces orthogonal to M 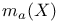 , minimum polynomial at a
, minimum polynomial at a 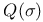 , quadric
, quadric 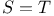 , S equals T
, S equals T 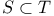 , S is contained in T
, S is contained in T 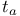 , translation
, translation 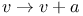
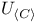 , complexification of real space U
, complexification of real space U 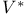 , dual space of V
, dual space of V 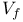 , F[X]-module defined by
, F[X]-module defined by 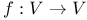
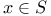 , x is an element of S
, x is an element of S ![$[S]_f$](/math_tex/7424b3f3da19d2094df1fab166b89e2582.gif) , submodule of
, submodule of 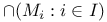 ,
, 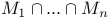 , intersection
, intersection 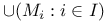 ,
, 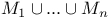 , union
, union 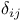 , Kronecker delta
, Kronecker delta 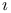 , canonical isomorphism
, canonical isomorphism 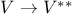
 , complex numbers
, complex numbers 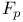 , integers modulo p
, integers modulo p  , rational numbers
, rational numbers  , real numbers
, real numbers  , integers
, integers 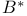 , dual proposition
, dual proposition 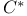 , dual configuration
, dual configuration 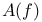 , mapping of affine geometries induced by
, mapping of affine geometries induced by 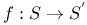
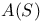 , affine geometry on coset S
, affine geometry on coset S 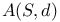 , euclidean geometry on coset S with distance d
, euclidean geometry on coset S with distance d 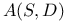 , similarity euclidean geometry on coset S with distance class D
, similarity euclidean geometry on coset S with distance class D 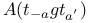 , affinity
, affinity 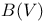 , bilinear forms on V
, bilinear forms on V 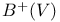 , symmetric bilinear forms on V
, symmetric bilinear forms on V 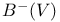 , skew-symmetric bilinear forms on V
, skew-symmetric bilinear forms on V 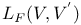 , linear mappings of V into
, linear mappings of V into 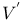
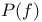 , mapping of projective geometries induced by
, mapping of projective geometries induced by 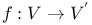
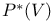 , dual geometry
, dual geometry 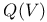 , quadratic forms on V
, quadratic forms on V 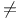 , is not equal to
, is not equal to 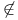 , is not an element of
, is not an element of 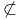 , is not contained in
, is not contained in 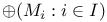 ,
, 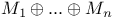 , direct sum
, direct sum 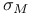 , restriction of
, restriction of  to subspace M
to subspace M 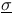 ,
, 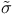 , linear mappings induced by the bilinear form
, linear mappings induced by the bilinear form 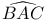 , angle
, angle 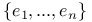 , standard basis of
, standard basis of 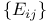 , standard basis of
, standard basis of 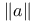 , norm of a
, norm of a ![$F[X]^n$](/math_tex/8c00c93bc7afc04ddad728c954a4c44b82.gif)