|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Elliot P.D.T.A. — Probabilistic Number Theory One |
|
|
 |
| Предметный указатель |
Marcinkiewicz 58
Marek 111
Matthews 12 185
Mean of a random variable 30
Measure 16
Measure probability 29 30 115—146
mellin 61 78 279 307 322
Mellin transform, M-transform 61 141 279 307 94—95 233 322—326
Mellin — Stieltjes 61 141
Mellin — Stieltjes transform 61 141 279 307
Mendelssohn, Fanny 111
Mendelssohn, Felix 111
Mendelssohn, Moses 112
Mendelssohn, Rebecka 111 112
Mertens 89
Metric, Levy 14 24
Minor Arcs, intervals 7 8 9
Mirsky 162 166
Model for multiplicative functions 140
Models for strongly additive functions 115—146
Modified-Levy representation 51
Moebius 85 251 254 282 301
Moebius inversion 85
Moments, determination by 60—61
Moments, method of 59
Montgomery 93 185 229 235 317
Montgomery and Vaughan 185
Mordell 213
Munroe 18
Natural boundary 100
Niederreiter and Kuipers 78
Norm, 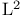 12 23 12 23
Norm, algebraic 114
Norm, operator 181 186
Normal law 52
Normal law (definition) 11
Normal number of prime factors 2
Normal order of an arithmetic function 2 14
Offord and Littlewood 217
Operator norm 181 186
Operator, adjoint of 181—182
Operator, Dirichlet-series type 186
Operator, dual of 12 181—182
Pan 184
Parseval 8 23 228 235 236
Parsevals' relation 8 23 228 235 236;
Partitions 2
Perfect numbers 4
Perron 94 95 322
Perron's theorem 94—95 322—326
Philipp 127
Plancherel 22 23
Plancherel's identity 23 228 235 236;
Plancherel's theory 22
Poincare 3
poisson 52
Poisson law 52—53 6
Polya — Vinogradov 154
Polya — Vinogradov inequality 154
Polya, Hardy and Littlewood 186
Postnikov 11 74 78
Prachar 90 91 92 95
Prime ideal theorem 94
Prime number theorem 10 90 145 254 283
Prime number theorem, elementary proof 10 90
Prime numbers in arithmetic progressions 90—92
Prime numbers, distribution 89
Primitive root, least positive 158
Probability measure 29 30 115—146
Probability space 29 115—146
Products of independent random variables 141 142 144
Proper distribution function 25
Purity of type 46 78 292
Quadratic Class Number 14 110—111 117
Quadratic residues, least pair of 153
Rado 214
Raikov 58 112 113
Ramanujan 1
Ramanujan and Hardy 2 3 5 13 14
Random variable 29
Random variable, infinitely divisible 49
Relations asymptotic 19—21
Renyi 3 9 12 24 47 92 93 183 184 218 3
Renyi and Turan 6
Richert and Halberstam 80 185
Riemann 96 97 154 338 341
Riemann hypothesis 97
Riemann zeta function 96
Riemann zeta function functional equation 97
Rogozin 32 78 218
Roth 12 184
Roth and Halberstam 77
Ryavec 283 289
Ryavec and Elliott 10 257 258 265 268 283 306
Ryavec and Erdos 268
Schmidt, R. 18 77
Schnirelmann 77 292 293 294 296
Schnirelmann density 77 293
| Schnirelmann sum 293
Schoenberg (Schonberg) 4 189 213 214
schur 214
Schwarz — Cauchy 42 68 135 149 150 151 160 161 164 168 174 196 197 201 202 234 243 246 271 300 304 317 338 339 345 348 349
Selberg 79 80 84 119 127 129 142 145 176 182 185 213
Selberg and Erdos 10 256
Selberg's sieve method 79—89 120—121 129 142 145 176 185 213
Shohat — Frechet 59 78
Siegel — Walfisz 91
Sierpinski 76
Sieve, Brun 4 9 80 129
Sieve, large 9 10 12 13 93 165 183—186 317
Sieve, Selberg 79—89 120—121 129 142 145 176 185 213
Skew — Hermitian form 166
Slowly decreasing functions 102
Slowly oscillating functions 18
Spectral radius 12 162
Spectral radius of Hermitian matrix, operator 12 162
Spemer 32 78 214 216 218
Sperner's Lemma 32 78 214 216 218
Stable law 11
Steinhaus 16 76 261 283
Stepanov 155
Stieltjes — Fourier 61 305
Stieltjes — Mellin 61 141
Stirling 34
Stolz 338
Stone — Weierstrass 307
Substitutions, group of 13
Sums of independent random variables, limit theorems 54
Surrealistic Continuity Theorem 265 269
Szuesz 224
Tauber 77 100 101 102 254 351 358
Tauberian theorem, Hardy and Littlewood 102 254 348 351 358
Tauberian theorem, Hardy and Littlewood (statement) 77
Tauberian theorem, Wiener — Ikehara 100—101
Taylor 104
Tchebycheff 3 36 44 192 235
Tchebycheff's inequality 3 192
Theodorescu and Hengartner 218
Three Series Theorem, Kolmogorov 37—38 77
Timofeev and Levin 10 12 257 258
Timofeev, Tuliaganov and Levin 274 275 280 281
Titchmarsh 10 22 58 59 70 90 94 95 97
Titchmarsh — Brun 90 120 135 160 161 213
Tjan 219
Total event 29
Truncated additive functions 5
Tuliaganov, Timofeev and Levin 274 275 280 281
Tunin and Erdoes inequality 75
Tunin — Kubilius inequality 6 13 147—186 192 199
Tunin — Kubilius inequality, dual of 13 147—186 194 335
Turan 3 4 5 6 147 180 181 182 185
Turan and Erdos 75
Turan and Renyi 6
Turan — Kubilius 6 13 147 152 158 173 182 185 192 199 218
TYPE 26
Uniform distribution (mod 1) 66 69
Uniform law (mod 1) 66
Uzdavinis 134
van Ardenne-Ehrenfest, de Bruijn and Korevaar 18 77
Variance, random variable 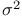 , , 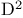 30—31 30—31
Vaughan and Montgomery 185
Vinogradov — Polya 154
Vinogradov — Polya inequality 154
Vinogradov, A. I. 92 93 184
Vinogradov, A. I. and Barban 122 126
Vinogradov, A. I., Barban and Levin 174
Vinogradov, I. M. 2 7 8 154 155
Viola and Forti 12 185 186 317
von Mangoldt 97 311
von Mangoldt's function 97 311
Walfisz and Landau 100
Walfisz — Siegel 91
Weak convergence of distribution functions 24 25
Weak convergence of distribution functions (mod 1) 65—68
Weak convergence of measures 24 30
Weierstrass — Stone 307
Weil 155
Weyl 69 75 284
Weyl's criterion 69
Weyl's criterion, quantitative 75
Wiener 68 100
Wiener — Ikehara 100 101 102
Wiener — Ikehara tauberian theorem 100—101
Wintner 3 10 59 78 254 285
Wintner and Erdos 4 10 187 214 254 280
Wintner and Jessen 46 78 193
Wintner — Erdoes theorem 187—224
Wirsing 10 11 90 144 225 226 227 254 255 256 273 331
Wolke 183
Wright and Hardy 85 89 108 112 118 133 134 224
Yong, Chi-hsing 77
Yosida 181
Z-module 289
Zeta function (Riemann) 97
Zolotarev 61 141 274 279 307
“Shifted primes” 9
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



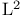
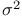 ,
,