|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Rosenberg S. — The Laplacian on a Riemannian manifold |
|
|
 |
| Предметный указатель |
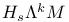 34 34
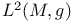 16 16
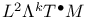 17 17
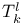 60 60
Acyclic representation 152
Analytic torsion 153
Asymptotic expansion 99
Atiyah — Singer index theorem 141
Basic elliptic estimate 36
Berezin integral 125
Betti number 42
Bianchi identity 60 127
Bismut — Lott theorem 163
Bochner's formula 75
Bochner's theorem 75
Cartan — Hadamard theorem 62
Characteristic class 129
Characteristic form 129
Chern character 138
Chern classes 132
Chern — Gauss — Bonnet theorem 112
Chern — Weil theory 126
Christoffel symbols 55
Compactness Theorem 25
Complete polarization 127
Conformal metric 16
Connected sum 135
Connection on a vector bundle 131
Connection, flat 153
Connection, Levi-Civita 64 65
Connection, one-forms 126
Contraction of a tensor 61
Convolution of functions 23
Covariant derivative 64
Critical path 78
Curl 22
Curvature of a general connection 131
Curvature, endomorphism 70
Curvature, Gaussian, for arbitrary surfaces 55
Curvature, Gaussian, for surfaces in 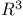 53 53
Curvature, Ricci 60 74
Curvature, scalar 61
Curvature, sectional 62
Curvature, two-forms 126
de Rham cohomology groups 40 42
de Rham's theorem 45
Divergence 18
Donaldson theory 133
Double form 34
Duhamel's formula 94
Einstein summation convention 14
Elliptic operator 139
Elliptic operator, determinant of 153
Elliptic operator, symbol matrix of 139
Euclidean space 11
Euler characteristic 49
Euler class 131
Euler form 112
Exponential map 80
Families index theorem 162
Fefferman — Graham invariant 148
Fermion calculus 67
Feynman — Kac formula 125
Fourier transform 22
Garding's inequality 36 75
Gauss map 53
Gauss — Bonnet theorem 56 111
Gauss' lemma 82
Geodesic 79
Geodesic, minimal 80
Global inner product 16
Gradient 17
Green's formula 156
Harmonic forms 46
Heat equation 5 27
Heat kernel for forms 99
Heat kernel for functions 98
Heat kernel on a manifold 27
Heat kernel on Euclidean space 6
Heat kernel on forms 34
Heat kernel on the circle 6
Heat kernel on the real line 6
Heat kernel, approximate on forms 114
Heat kernel, approximate on functions 114
Heat kernel, asymptotic expansion 99
Heat kernel, dependence on metric 155
Heat kernel, pointwise convergence 89
Heat kernel, positivity 106
Heat kernel, symmetry 8
Heat operator 27
Heat operator, semigroup property 28
Higher torsion classes 164
Higher torsion forms 164
Hirzebruch L-polynomial 135
| Hirzebruch proportionality 113
Hirzebruch signature theorem 136
Hirzebruch — Riemann — Roch theorem 139
Hodge decomposition theorem 38
Hodge inner product 21
Hodge star operator 19
Hodge theorem 46
Hodge theorem for forms 34 37
Hodge theorem for functions 32
Holonomy group 67
Homotopy equivalence 42
Hopf conjectures 62 113
Hopf — Rinow theorem 80
Horizontal distribution 162
Index bundle 161
Index o? an operator 133
Integrability condition 40 54 57
Integration along the fibers 162
Interior product 67
Intersection pairing 132
Invariant polynomial 127
Isospectral manifolds 100
Jacobi equation 85
Jacobi fields 85
Jacobi's formula 9
Join 51
Kronecker delta 15
Laplacian in polar coordinates 87
Laplacian of an exact complex 152
Laplacian on forms 33
Laplacian on functions 18 19 21
Laplacian on twisted forms 153
Laplacian, Bochner 72 125
Laplacian, conformal 145
Laplacian-type operator 142
Lie bracket 126
Local frame 126
Lohkamp's theorem 61
McKean — Singer lemma 110
Mellin transform 143
Myers' Theorem 61 75
Operator, compact 2
Operator, elliptic 139
Operator, Lapladan-type 142
Orthonormal frame 70
Parallel translation 66 67
Parametrix 93
Piaffian 129 130
Pontrjagin classes 129
R-torsion see "Analytic torsion"
Rayleigh — Ritz formula 159
Reidemeister torsion 152
Riemami's theorem 57
Riemann curvature tensor 57 67
Riemannian distance 13
Riemannian manifold 11
Riemannian manifold, isometry of 11
Riemannian metric 11
Riemannian metric, flat 57
Riemannian metric, induced 11
Riemannian normal coordinates 82
Riemannian polar coordinate 82
Schroedinger operator 125
Signature 133
Signature operator 133
Signature operator, twisted 138 161
Sobolev embedding theorem 24
Sobolev spaces for forms 33
Sobolev spaces for functions on Euclidean space 22
Sobolev spaces for Junctions on manifolds 26
Spectral theorem 2
Spectrum 2 4
Sunada's theorem 149
Supertrace 69
Symbol bundle 141
Symbol matrix 139
Synchronous frame 73
Synge's theorem 62
Tangent bundle along the fibers 162
Theorema Egreglum 55
Todd polynomial 138
Torsion of an exact complex 152
Traceless Ricci tensor 148
Transport equations 92
Universal polynomials 83
Variation vector field 79
Virtual bundle 140 101
Volume 15
Volume form 15
Weierstrass approximation theorem 7
Weitzenboeck formula 72
Weyl tenBor 148
Wiener measure 126
Zeta function 143 153
Zeta function, meromorphic continuation 143
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте