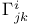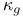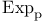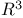|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Morgan F. — Riemannian geometry, a beginners guide |
|
|
 |
| Предметный указатель |
Arc length 18 101
Area, and Gauss curvature 22
Bending 22
Bianchi's first identity 35 41
Black hole 60
Bonnet's theorem 77 84
Calibration 99
Catenoid 15 20
Chain rule 17
Christoffel symbols 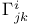 40 102 40 102
Co variant derivative 36 42 103
Co variant derivative, along curve 48
Comparison theorem of Rauch 88
complete 77
Conjugate points 82
Conjugate points, and sectional curvature 83
Conjugate points, and shortest geodesies 83
Connection 41
Contravariant 40
Convex norm 89 92
coordinates 14 39
Coordinates, normal 78
Costa's surface 17
Covariant 40
Crystals 89
Curvature 1 5 see “Gauss “Mean “Principal “Ricci “Riemannian “Scalar “Sectional
Curvature of curves, generalized  93 97 93 97
Curvature of curves, geodesic 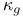 47 47
Curvature of curves, radius of 5
Curvature vector k of curve 5 47 101
CURVES 5 see “Geodesics”
Curves, curvature vector k 5
Curves, isoperimetric 93 95 97
Curves, normal vector n 5
Curves, tangent vector T 5
Cut points 83
Cylinder 22 84
Diameter 77
Diameter, Bonnet's theorem 84
Diameter, Myers theorem 87
Einstein tensor Gj 58
Ellipsoid 23
Enneper's surface 16
Equivalence principle 56 58
Euler characteristic  67 71 67 71
Euler's formula 13
Exponential map 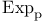 77 82 77 82
Exponential map 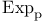 , and sectional curvature 83 , and sectional curvature 83
Extrinsic 1
Fermat problem 98
First fundamental form 18
Gauss curvature G 1 13 19 26 27 42 101 102 103
Gauss curvature G, and area 22
Gauss curvature G, and parallel transport 72
Gauss curvature G, constant 50 87
Gauss curvature G, in local coordinates 72
Gauss curvature G, of geodesic triangle 66
Gauss curvature G, of hypersurface 71
Gauss curvature G, of projections 26
Gauss map n 69 71
Gauss — Bonnet formula 65
Gauss — Bonnet formula, proof in 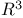 74 74
Gauss — Bonnet theorem 65 67—69
Gauss — Bonnet theorem, proof in  74 74
Gauss — Bonnet — Chern theorem 71
Gauss's Theorema Egregium 2 21 65
General relativity 55—63
Geodesic triangle 66 74
Geodesies 47 77
Geodesies, converge for positive curvature 51 58 85
Geodesies, existence and uniqueness 48
Geodesies, formula for 49 102
Geodesies, hyperbolic space 50
Geodesies, relativity 57
Geodesies, sphere 53 54
Geometric measure theory 93
Geometry, bounded 84
Geometry, global 77
Geometry, Riemannian 1 56
Gradient 103
Graph, curve 5
Graph, surface 18 19 102
Gravity 56 58
Helicoid 15 23
Helix 8
Hopf — Rinow theorem 48 79
Hyperbolic geometry 49 87
| Hypersurfaces 32 33
Injectivity radius 84
INTRINSIC 2 18 21 22 39—54
Isoperimetric problem 93—98
Jacobi field 82
Laplacian 103
Length 15 18 101
Lunes 74 75
Mean curvature H 1 13 19 32 101 102
Mean curvature vector H 26 27 32 102
Mercury 55 60—62
Metric  18 57 101 18 57 101
Metric  , I to first order 21 42 78 , I to first order 21 42 78
Metric  , Lorentz 57 60 , Lorentz 57 60
Metric  , Schwarzschild 58 60 , Schwarzschild 58 60
Minimal surfaces 14—17
Myers theorem 87
Nash embedding theorem 39 71
networks 98—100
Non-Euclidean geometry 50
Normal coordinates 78
Normal n, to curve 5
Normal n, to hypersurface 32
Normal n, to surface 11
Norms 89—100
Norms, crystalline 98
Norms, first variation of 93
Norms, Manhattan 99
Norms, rectilinear 99
Orthogonal group SO(n) 78 79
Osculating circle 5
Parallel transport 72 74
Parallel transport, and second variation 85 86
Precession 55
Pressure 14
Principal curvatures 11 13 19 26
Principal directions 13
Projection 44
Proper time  58 58
Rauch comparison theorem 88
Ricci curvature 35 41 103
Ricci curvature, Myers theorem 87
Ricci's identity 43
Ricci's lemma 43
Riemannian curvature tensor 34 41 102
Riemannian curvature tensor, and inequality of mixed partials 43
Riemannian curvature tensor, and parallel transport 72—73
Scalar curvature R 36 42 103
Scalar curvature R, and volume 42
Scherk's surface 15
Schwartz symmetrization 94
Second fundamental form II 12 18 32 34
Second fundamental tensor II 25 31
Sectional curvature 33 42 77 103
Sectional curvature, Bonnet's theorem 84
Sectional curvature, conjugate points 83
Sectional curvature, constant 50 87
Sectional curvature, diameter 84
Sectional curvature, exponential map 83
Sectional curvature, of projections 33
Sectional curvature, Rauch comparison theorem 88
Sectional curvature, sphere theorem 87
Sectional curvature, weighted average of axis curvatures 33
Slice 11
Smokestack 6—10
Soap films 99
Special relativity 55 57
Sphere 18 23 47 53 67 68 69 73 75 82 87
Sphere theorem 87
Spherical trigonometry 67
Steiner problem 98
Stokes's theorem 92
Strake 6—10
Surface of revolution 23
Surfaces, in 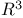 11 11
Surfaces, in 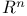 25 25
Symmetries 34 41
Tangent space  11 11
Tangent vector T to curve 5
Torsion 41
Torus 51
Variation, of curve 6 7 48 93
Variation, of surface 13 26 32
Variation, second, of curve 85 86 87
Volume, and scalar curvature 42
Weingarten map Dn 69 71
Wulff shape 94
Yamabe problem 42
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте