|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Isham J. — Modern Differential Geometry for Physics |
|
|
 |
| Предметный указатель |
Topology, cofinite 36 54
Topology, component of 61
Topology, connected 61
Topology, definition of 13 32 35
Topology, discrete 43 54
Topology, finer see Topology stronger
Topology, first countable 33
Topology, Hausdorff 53
Topology, identification 50 53
Topology, indiscrete 43
Topology, induced 50
Topology, lattice structure on 52
Topology, lattice structure on open sets 40
Topology, of a metric space 13
Topology, paracompact 231 242
Topology, product 36
Topology, separation axioms 52
Topology, stronger 42
Topology, subbase of 35
Topology, subspace 50
Topology, weaker 42
Topos theory 42
Torus 67
Upper set 27 36
Vector bundle 123 248
| Vector bundle, 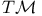 as an example of 77 as an example of 77
Vector bundle, map between pair of 248
Vector field, 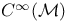 -module structure on set of 99 -module structure on set of 99
Vector field, as derivation of ring  99 99
Vector field, commutator of pair of 102
Vector field, complete 109
Vector field, components of 100
Vector field, definition of 97
Vector field, h-related pair of 105
Vector field, horizontal lift of 262
Vector field, induced 114
Vector field, induced by one-parameter subgroup 191
Vector field, integral curve of 108
Vector field, left-invariant 158
Vector field, Lie derivative of see Lie derivative vector
Vector field, local flow of 115
Vector field, restriction to open subset 98
Vector field, right-invariant 3 58
Vector field, vector space structure on set of 99
Vector space, topological 63 122
Vector, horizontal 256
Vector, vertical 254
Vertical subspace 268
Vertical vector see Vector vertical
Wilson loop 266
Yang — Mills theory 16 201 207 222 224 229 231 239 256 265 271
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



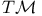 as an example of
as an example of 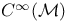 -module structure on set of
-module structure on set of 