|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Бурбаки Н. — Интегрирование. Меры на локально компактных пространствах. Продолжение меры. Интегрирование мер. Меры на отделимых пространствах |
|
|
 |
| Предметный указатель |
 -адаптированная ( -адаптированная ( -приспособленная) мера V.4.1 -приспособленная) мера V.4.1
 -измеримая функция IV.5.1 -измеримая функция IV.5.1
 -измеримое множество IV.5.1 -измеримое множество IV.5.1
 -интегрируемая функция IV.4.1 -интегрируемая функция IV.4.1
 -интегрируемое множество IV.4.5 -интегрируемое множество IV.4.5
 -максимум IV.6.2 -максимум IV.6.2
 -минимум IV.6.2 -минимум IV.6.2
 -пренебрежимая функция IV.2.1 IV.2.4 -пренебрежимая функция IV.2.1 IV.2.4
 -пренебрежимое множество IV.2.2 -пренебрежимое множество IV.2.2
 -собственное отображение V.6.1 V.6.4 IX.2.3 -собственное отображение V.6.1 V.6.4 IX.2.3
 -согласованное отображение V.3.1 -согласованное отображение V.3.1
 -эквивалентные функции IV.2.4 -эквивалентные функции IV.2.4
H-экстремальная точка IV.7.3
Абсолютное значение меры III.1.6
Аддитивная функция множества IV.4.9 IX.3.2
Алгебра подмножеств (клан подмножеств)  -алгебра (тело) IV.4.9 -алгебра (тело) IV.4.9
Ассоциированная промера IX.6.1
Атомическая мера III.1.3
Базис меры V.5.2 IX.2.2
Барицентр меры IV.7.1
Бишопа теорема IV.7.5
Бохнера теорема IX.6.12
Вариация меры IX.6.5
Верхний интеграл IX.1.9
Винера мера IX.6.7
Внешняя мера IV.1.2 IV.1.4 IX.1.9
Гауссова каноническая промера на действительном гильбертовом пространстве IX.6.6
Гауссова мера IX.6.5
Гауссова мера с матрицей ковариации C IX.6.6
Гауссова промера с вариацией Q IX.6.5
Гауссова промера с ковариацией К IX.6.6
Гёльдера неравенство IV.6.4
Гильберта — Шмидта отображение IX добавление
Двойной интеграл III.4.1
Дезинтегрирование меры V.6.6 IX.2.7
Действительная мера III.1.5
Действительная часть меры IX.1.5
Дирака мера III.1.3
Диффузия ограниченная V.3.5
Егорова теорема IV.5.4
Заграждение IX.1.1
Заграждение индуцированное IX.1.1
Заграждение образ IX.1.1
Заграждение ограниченное IX.1.1
Заграждение, локально ограниченное IX.1.1
Заграждение, сосредоточенное на подмножестве IX.1.1
Измельчение IX.1.8
Измеримая функция IV.5.1 IX.1.5
Измеримая функция, определенная на измеримом подмножестве IV.5.10
Измеримое множество IV.5.1 IX.1.5
Инвариантная мера при гомеоморфизме III.1.3
Индуцированная мера IX.2.1
Индуцированная мера на локально компактное подпространство IV.5.7
Индуцированная мера на открытое множество III.2.1
Индуцированное заграждение IX.1.1
Интеграл верхний IV.1.1 IV.1.3 IV.4 упражнение IX.1.9
Интеграл верхний существенный I.1.1 IX.1.2
Интеграл двойной III.4.1
Интеграл кратный III.4.4
Интеграл нижний IV.4 упражнение
Интеграл от интегрируемой функции IV.4.1
Интеграл от непрерывной функции с компактным носителем III.1.3
Интеграл от слабо непрерывной финитной функции III.3.1
Интеграл от существенно интегрируемой функции V.1.3
Интеграл от функции IX.1.10
Интеграл от функции на A V.5.3
Интегрирование по частям V.8 упражнение
Интегрируемая функция IV.4.1 IX.1.10
Интегрируемое множество IV.4.5 IX.1.9
Квадратичная форма ядерная IX добавление
Класс эквивалентности функций относительно меры IV.2.4 IV.2.5 IV.5.2
Ковариация гауссовой промеры на 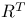 IX.6.6 IX.6.6
Комплексная мера III.1.3
Конечная почти всюду функция IV.2.6
Кратный интеграл III.4.4
Лапласа преобразование IX.5.7
Лебега мера III.1.3 III.4.1 III.4.4
Лебега теорема IV.3.7 IV.4.3
Лебега теорема о разбиении V.5.7
Локально интегрируемая функция IX.2.2
Локально ограниченная функция множества IX.3.2
Локально ограниченное заграждение IX.1.1
Локально почти всюду IX.1.4
Локально пренебрежимая функция IV.5.2 IX.1.4
Локально пренебрежимое множество IV.5.2 IX.1.4
Локально счетное множество подмножеств IV.5.9
Локально счетное семейство функций V.5.4
Максимум по мере IV.6.2
Мера III.1.3 IX.1.2
Мера атомическая III.1.3
Мера Винера IX.6.7
Мера внешняя IV.1.2 IV.1.4
Мера внешняя множества IX.1.9
Мера внутренняя IV.4 упражнение
Мера действительная III.1.5
Мера Дирака III.1.3
Мера дискретная III.1.3
Мера зауссова с вариацией Q IX.6.5
Мера инвариантная при гомеоморфизме III.1.3
Мера индуцированная III.2.1 IV.5.7 IX.2.1
Мера комплексная III.1.3
Мера Лебега III.1.3 III.4.1 III.4.4
Мера модерантная IX.1.9
Мера ограниченная III.1.8 IX.1.2
Мера плотности g (соотв. f) относительно  ) III.1.4 IX.2.2 ) III.1.4 IX.2.2
Мера положительная III.1.5
Мера с базисом  IX.2.2 IX.2.2
Мера с матрицей ковариации IX.6.6
Мера сопряженная III.1.5
Мера точечная III.2.4
Мера, не содержащая массы на открытом множестве III.2.2
Мера, определенная посредством единичной массы в точке III.1.3
Мера, определенная посредством масс III.1.3
Мера-образ IX.2.3
Мера-произведение III.4.1 IX.2.5
Минимум по мере IV.6.2
Минковского неравенство IV.3.1
Минлоса теорема IX.6.10
Мнимая часть меры III.1.5
Множество  -интегрируемое IV.4.5 -интегрируемое IV.4.5
Множество  -плотное (компактных подмножеств) IV.5.8 -плотное (компактных подмножеств) IV.5.8
Множество  -пренебрежимое IV.2.2 -пренебрежимое IV.2.2
Множество измеримое IX.1.5
Множество интегрируемое IV.4.5 IX.1.9
Множество квадрируемое IV.5.17
Множество локально  -пренебрежимое IV.5.2 -пренебрежимое IV.5.2
Множество локально пренебрежимое IV.5.2 IX.1.4
Множество локально счетное (подмножеств) IV.5.9
Множество модерантное IX.1.9
Множество пренебрежимое IV.2.2 IX.1.9
Множество равностепенно интегрируемое IV.5.11
Множество универсально измеримое IX.3.3
Множество, несущее меру V.5.7
Множество, строго компактное в  III.1.1 III.1.1
Модерантная мера IX.1.9
Модерантная функция IX.1.9
Модерантное множество IX.1.9
Непрерывная мера (рассеянная) V.5.10
Неравенство Гёльдера IV.6.4
Неравенство М. Рисса IV.6.18
Неравенство Минковского IV.3.1
Неравенство о среднем IV.6.2
Неравенство Харди IV.6.19
Норма меры III.1.8
Носитель меры III.2.2 IX.1.6
Носитель функции III.1.1
Образ заграждения IX.1.1
| Образ меры V.6.1 IX.2.3
Образ промеры IX.6.2
Ограниченная мера III.1.8 IX.1.2
Ограниченная функция множества IX.3.2
Ортогональная система Хаара IV.6.17
Отображение Гильберта — Шмидта IX добавление
Отображение скалярно слабо непрерывное III.3.1
Отображение скалярно финитное III.3.1
Пара  -адаптированная V.4.1 -адаптированная V.4.1
Плотность III.1.4
Плотность меры (относительно другой) V.5.2 IX.2.2
Подмоноид полный IX.5.7
Подпроективная система мер IX.4.2
Полная масса ограниченной меры III.1.8 IV.4.7
Полная масса промеры IX.6.1
Положительная мера III.1.5 IX.1.2
Положительная предмера IX.1.2
Последовательность, сходящаяся почти всюду IV.2.5
Предельное распределение последовательности III.2.упр 5
Предмера IX.1.2
Предмера действительная IX.1.2
Предмера положительная IX.1.2
Пренебрежимая функция IV.2.1 IX.1.9
Пренебрежимое множество IV.2.2 IX.1.9
Преобразование Лапласа меры IX.5.7
Принцип локализации для измеримых функций IV.5.2
Принцип локализации для мер III.2.1
Проективная система мер III.4.5 IX.4.2
Проективный предел мер IX.4.2
Произведение двух мер III.4.1 IX.2.5
Произведение конечного числа мер III.4.4
Произведение меры на непрерывную функцию III.1.4
Произведение семейства мер IX.4.3
Произведение семейства положительных мер III.4.6
Производящая функция последовательности IX.5.7
Промера IX.6.1
Промера, ассоциированная с мерой IX.6.1
Промера-образ IX.6.2
Прообраз меры при локальном гомеоморфизме V.6.6
Пространство радоново IX.3.3
Пространство сильно радоново IX.3.3
Пространство ядерное IX.6.10
Прохорова теорема IX.4.2
Прохорова условие IX.4.2 IX.5.5
Равномерная структура сходимости по мере IV.5.11
Равнораспределенная по мере последовательность III.2 упражнение
Равностепенно интегрируемое множество IV.5.11
Радоново пространство IX.3.3
Разбиение на слои V.6.6
Размещенная измеримая функция IV.5.5
Размещенная функция IV.4.9
Сазонова топология IX.6.10
Свойство, верное локально почти всюду IV.5.2
Свойство, верное почти всюду IV.2.3
Сильно радоново пространство IX.3.3
Сингулярные меры (независимые) V.5.7
Скалярно финитная функция III.3.1
Слабо непрерывное отображение III.3.1
След квадратичной формы (относительно другой) IX добавление
Сопряженная мера III.1.5
Сопряженное к линейному отображению IX добавление
Сопряженные показатели IV.6.4
Сосредоточенная мера (на множестве) V.5.7
Сосредоточенная мера на подмножестве IX.1.4
Среднее функции III.1.8
Строго компактное множество III.1.1
Сужение меры на открытое множество III.2.1
Сумма семейства мер IX.1.7
Суммируемое семейство положительных мер V.2.1
Существенно  -интегрируемая функция V.1.3 -интегрируемая функция V.1.3
Существенно  -интегрируемое множество V.1.3 -интегрируемое множество V.1.3
Существенно интегрируемая функция на A V.5.3
Существенный верхний интеграл V.1.1 IX.1.2
Сходимость в среднем IV.3.3
Сходимость в среднем порядка IV.3.3
Сходимость в среднем, средняя квадратичная IV.3.3
Сходимость компактная (в пространстве мер) III.1.10
Сходимость по мере IV.5.11
Сходимость строго компактная (в пространстве мер) III.1.10
Сходимость широкая III.1.9
Счетно аддитивная функция множества IX.3.2
Тело см. « -алгебра» -алгебра»
Теорема Бишопа IV.7.5
Теорема Бохнера IX.6.12
Теорема Егорова IV.5.4
Теорема Крейна IV.7 упражнение
Теорема Лебега IV.3.76 IV.4.3
Теорема Лебега о разбиении V.5.7
Теорема Минлоса IX.6.10
Теорема о счетной выпуклости IV.3.2
Теорема Прохорова IX.4.2
Теорема Шоке IV.7.2 IV.7.б
Топология компактной сходимости III.1.1Р
Топология Сазонова IX.6.10
Топология сходимости в среднем IV.3.3
Топология сходимости по мере IV.5.11
Топология узкая IX.5.3
Топология широкая III.1.9
Точечная мера III.2.4
Точка 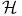 -экстремальная IV.7.3 -экстремальная IV.7.3
Убывающая перестановка функции IV.5 упражнение
Узкая топология IX.5.3
Универсально измеримая функция IX.2.7
Универсально измеримое множество V.3.4 IX.3.3
Ф-размещенная функция IV.4.9
Функции равноизмеримые IV.5 упражнение
Функция  -измеримая IV.5.1 -измеримая IV.5.1
Функция  -измеримая на А V.5.3 -измеримая на А V.5.3
Функция  -модерантная V.1.2 -модерантная V.1.2
Функция  -пренебрежимая IV.2.4 -пренебрежимая IV.2.4
Функция измеримая IV.5.1 IX.1.5
Функция интегрируемая IX.1.10
Функция Лебега IV.6 упражнение
Функция локально  -пренебрежимая IV.5.2 -пренебрежимая IV.5.2
Функция локально интегрируемая V.5.1 IX.2.2
Функция локально интегрируемая на A V5.3
Функция локально пренебрежимая IV.5.2
Функция множества аддитивная IV.4.9
Функция множества внутренне регулярная IX.3.2
Функция множества ограниченная IX.3.2
Функция множества, локально ограниченная IX.3.2
Функция модерантная IX.1.9
Функция положительного типа IX.6.12
Функция пренебрежимая IV.2.1 IX.1.9
Функция размещенная IV.4.9
Функция счетно аддитивная IX.3.2
Функция Ф-размещенная IV.4.9
Функция, зависящая от конечного числа переменных III.4.6
Функция, интегрируемая с p-й степенью IV.3.4
Функция, ограниченная по мере IV.8.2 IV.6.3
Функция, определенная локально почти всюду IV.5.2
Функция, определенная почти всюду IV.2.5
Функция, скалярно существенно интегрируемая V.3.1
Функция, существенно интегрируемая V.1.3 IX.1.10
Функция, существенно интегрируемая с p-й степенью V.1.3
Функция, универсально измеримая V.3.4 IX.2.7
Функция, широко  -измеримая V.3.1 -измеримая V.3.1
Функция, широко непрерывная V.3.1
Фурье преобразование промеры IX.6.3
Характер моноида IX.5.7
Широкая топология III.1.9
Шоке теорема IV.7.2 IV.7.6
Эквивалентные меры V.5.б
Эквивалентные функции IV.2.4
Ядерная квадратичная форма IX добавление
Ядерное пространство IX.6.10
Ядро положительного типа IX.б б
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -адаптированная (
-адаптированная ( -алгебра (тело)
-алгебра (тело) 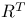

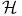 -экстремальная
-экстремальная