|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Kulikov V. — Mixed Hodge Structures and Singularities |
|
|
 |
| Предметный указатель |
![$B_{[Y]X}$](/math_tex/bf077cefd5e00b85ce4fe1af645c9dbe82.gif) (II.4.3.3) 85 (II.4.3.3) 85
 (II.2.5.6) 68 (II.2.5.6) 68
 (1.9.4.1) (II.6.1.6) 96 (1.9.4.1) (II.6.1.6) 96
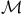 (II.6.1.1) 95 (II.6.1.1) 95
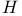 (I.1.3.1) 2 (I.1.3.1) 2
 (I.4.4.1) (I.5.3.2) 24 26 (I.4.4.1) (I.5.3.2) 24 26
 (I.3.3.4) (I.5.3.2) 12 26 (I.3.3.4) (I.5.3.2) 12 26
 (I.5.1.3) (I.5.3.2) 24 26 (I.5.1.3) (I.5.3.2) 24 26
 (II.5.2.3) 90 (II.5.2.3) 90
 (I.2.1.1) 2 (I.2.1.1) 2
 (I.2.1.1) 2 (I.2.1.1) 2
Cohomology, deRham (I.3.2.3) 11
Cohomology, Koszul (I.4.3.2) 18
Commutator rule (I.7.7.5) 35
Connection, canonical (I.2.5.3) 7
Connection, coefficients (I.2.3.5) 6
Connection, dual (I.2.6.1) 8
Connection, Gauss — Manin (I.1.3.1) 2
Connection, in the pair (I.4.4.3) 20
Connection, meromorphic (I.4.5.1) 20
Connection, on a sheaf (I.2.1.1)3
Connection, regular singular (I.7.7.1) 39
Covariant derivative (I.2.2.1) 4
Covariant differentiation (I.2.1.1) 4
De Rham cohomology (I.3.2.3) 11
de Rham complex (I.2.4.4) 7
Decomposition, block (II.6.1.1)95
Decomposition, of a meromorphic connection (II.6.2.5) 97
Decomposition, root (II.6.2.4) 97
Degree of spectrum (II.8.9.3) 130
Elemenrary section ![$s[A,\alpha]$](/math_tex/3ebdb4867604a98c77cf95e36171001a82.gif) (II.6.4.5) 100 (II.6.4.5) 100
Extension, canonical (II.2.6.4) (II.6.3.7) 98
Fibre, canonical (II.2.4.6) (II-2.4.8) 66
Fibre, Milnor (I.1.1.1)1
Filtration, Hodge (II.1.1.2) (II.1.3.1)60
Filtration, limit Hodge according to Scherk — Steenbrink (II.7.2.1) (II.7.3.2) 108
Filtration, limit Hodge according to Schmid (II.2.5.8) 68
Filtration, limit Hodge according to Steenbrink (II.3.2.4) (II.3.4.4) 79
Filtration, limit Hodge according to Varchenko (II.7.5.1) 111
Filtration, Newton (II.8.5.3) 122
Filtration, of a nilpotent operator (II.2.7.1) 71
Filtration, on a quotient (II.8.4.5) 120
Filtration, pole order (II.4.2.5) (II.4.5.1) 87
Filtration, V*- (II.6.3.3) 98
Filtration, weight (II.1.3.1) 61
Framed system of linear differential equations (III.5.1.3) 173
Gauss — Manin connection (I.1.3.1) 2
Gauss — Manin differential system (II.5.2.3) 90
Gysin exact sequence (II.4.1.1) 82
Hertling's invariants (III.5.2.5) (III.5.3.3) 178
Hodge filtration (II.1.1.2) (II.1.3.1) 61
Hodge numbers (II.1.3.2) 61
Hodge structure (II.1.1.1) 60
Hodge structure, polarized (II.1.2.1) 61
Jacobi algebra = Milnor algebra (I.4.3.5) 18
Join of singularities (II.8.7.1) 127
Key-lemma (I.7.6.2) 38
Koszul cohomology (I.4.3.2) (I.10.7.1)18
Koszul complex (I.4.3.1) 17
Lattice, Brieskorn (I.5.1.3) 24
Lattice, canonical (II.6.3.6) 98
| Lattice, in a vector space (I.4.5.5) 20
Lattice, saturated (I.7.7.2) 39
Leading part of  (II.6.3.2) 98 (II.6.3.2) 98
Leibniz identity (I.2.1.1) 3
Leray operator (I.4.1.5) 15
Leray residue theorem (I.4.1.6) 16
Limit, MHS (II.2.8.1) (II.3.2.7) 76
Limit, monodromy (I.7.8.1) 41
MHS morphism (II.1.3.3) 62
MHS-period map (III.3.6.5) 164
Milnor algebra (I.4.3.5) 18
Milnor cohomological fibration (I.1.2.1) (I.2.6.1)2
Milnor fibration (I.1.1.1) 1
Milnor fibre (I.1.1.1) 1
Milnor homological fibration (I.1.2.1) (I.2.6.1)2
Milnor number (I.1.4.5) (I.10.1.1) 51
Monodromy, horizontal (II.8.11.9) (III.5.2.1) 175
Monodromy, logarithm of the unipotent part (II.2.5.6) 68
Monodromy, supplement (II.3.5.10) 81
Monodromy, theorem (I.9.1.1) (II.3.5.9) 81
Monodromy, transformation (I.1.4.4) 3
Monodromy, vertical (II.8.11.9) 137
Order function (II.8.4.5) 120
Order function 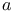 (II.6.3.1) 98 (II.6.3.1) 98
Order of a geometric section (III.2.4.2) 150
Order of an elements  (II.6.3.1) 98 (II.6.3.1) 98
Order, Newton (II.8.4.1) (II.8.5.2) 122
Period map (II.2.3.4) 64
Period map, defined by embedding of Brieskorn lattices (III.3.2.5) 153
Period map, defined by MHS in vanishing cohomology (III.3.6.5) 164
Period map, MHS (III.3.6.5) 164
Period matrix (I.8.1.6) 43
Period of a differential form (I.8.1.1) 42
Period space (II.2.3.3) 64
Period space  (III.3.2.8) 154 (III.3.2.8) 154
Period space  (III.3.2.5) 153 (III.3.2.5) 153
Period space for Hodge filtrations  (III.3.6.4) 164 (III.3.6.4) 164
Picard — Fuchs equation (I.8.1.5) (III.5.1.1) 172
Picard — Fuchs singularity (III.5.1.5) 174
Regularity theorem (I.8.2.1) 44
Residue Leray theorem (I.4.1.6) 16
Residue of a meromorphic connection (I.7.7.4) 39
Residue of a system (I.7.5.1) 37
Root, component of order a (II.6.2.6) 97
Root, decomposition of 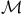 (II.6.2.5) 97 (II.6.2.5) 97
Section, elementary of order  (II.6.4.5) 100 (II.6.4.5) 100
Section, geometric (I.5.1.6) (III. 145
Section, horizontal (I.2.3.7) 6
Semicomtinuity domain (II.8.9.7) 131
Sheaf of nearby cycles (II.8.11.8) 136
Sheaf of vanishing cycles (II.8.11.8) 136
Singular point of a differential equation, regular (I.7.4.1) 36
Singular point of a differential equation, simple (I.7.5.1) 36
Spectral multiplicities (II.8.1.4) 116
Spectral numbers (II.8.1.4) 116
Spectrum of a singularity (II.8.1.4) (II.8.10.4)116 133
Spectrum pairs (II.8.2.1) 117
Spectrum properties (II.8.3.2) (II.8.3.3)
Torelli theorem infinitesimal (III.4.3.1) 169
Variation of Hodge structure (II.2.2.1) 63
Yomdin series (II.8.11.1) 134
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



![$B_{[Y]X}$](/math_tex/bf077cefd5e00b85ce4fe1af645c9dbe82.gif)








![$s[A,\alpha]$](/math_tex/3ebdb4867604a98c77cf95e36171001a82.gif)