|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ayoub R. — An Introduction to the Analytic Theory of Numbers |
|
|
 |
| Предметный указатель |
"Major arcs" 210 275
"Minor arcs" 210
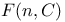 282 282
 298 298
 282 282
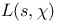 23 23
 135 135
 14 14
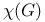 8 8
 8 8
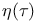 145 145
 240 240
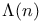 72 72
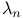 147 147
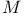 214 214
 211 211
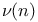 105 105
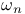 139 139
 329 329
 329 329
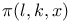 120 120
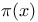 38 38
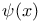 73 73
 146 146
 76 76
 105 105
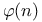 8 8
 3 3
 282 282
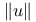 223 223
((x)) 168
A(q) 211
Abeiian group 8 12 10 198 278
Abeiian theorem 86
Abel 39
Abel method of partial summation 14
Abel summation 19
Abel’s theorem 141
Abscissa of absolute convergence 33 53
Abscissa of convergence 17 18 19 23 27 33 34 50 52 55 87 125 287
Analytic class field theory 30
Arithmetic progressions 30
Asymptotic formula 144 203 235—245
Axer’s theorem 127 132
bessel 151 185
Binary quadratic forms 27
Brauer, R. 351
Brun, Viggo 39
Cahen 130
Cauchy 33 49 51 52 54 55 66 74 84 86 136
Cauchy — Schwarz inequality 253 259
Cauchy’s Theorem 92 144 145 156 169 185 207 208 210 223 366
Cayley 349
CHARACTER 6 10 12
Character, complex 26
Character, conjugate 28
Characters 8 9 12 302—319
Characters for residue classes 32
Characters, induced 303
Characters, primitive 305—307
Circle of convergence 17
Class number 282 296
Completely multiplicative 4 6 23
Conductor 307
Convex body 279
Convex set 279
Cyclotomic equations 34
Cyclotomic field 27 35
D(n) 105
Davenport, Ann 211
Davenport, H. 242
De La Vallee Poussin 46 61 77 130 131
Dedekind 145 155 168 176 349 350
Dedekind cut 17
Dirichlet 1 3 6 13 14 17 21 23 24 27 29 35 36 48 50 52 56 131 136 235 349
Dirichlet density 29
Dirichlet L-functions 277—351
Dirichlet’s Theorem 1—36
Discriminant 288
Discriminant, fundamental 310
Discriminant, prime 310
E(n) 103
Encke 129
Equivalence of ideals 277
Erathosthenes 39
Erdoes 37
Euclid 1 2 3 30 34
Euclid’s theorem 24 31
Euler 1 3 5 6 7 8 24 25 37 43 102 128 129 130 131 136 139 140 165 195 203
Euler  -function 103 -function 103
Euler gamma function 90
Euler — Fermat theorem 28
Euler — Lagrange 135 275
Euler — MacLaurin 19 33 42 43 44 359
F(X) 136
Farey arcs 181
Farey dissection 178—181 212 214
Farey fractions 201 204
Farey series 178 179 213
Fejer kernel 94
Fermat 31
Ford circle 201
FOURIER 215 216
Fourier series 346
Fourier transform 49 94
g(k) 207
Gamma function 353 361 364
Gauss 35 39 47 129 277 320 327 349 350 351
Gauss — Dirtchlet 298—302
Gauss — Heilbronn 327
Gauss — Lengendre 2
Gaussian sums 302—319 368
Goldbach 135
Goldbach’s problem 268
| H(a,q) 220
h(d) 278
hadamard 46 56 78 130
Hall, Marshall 10
Halphen 130
Hankel transform 357
Hardy 35 145 1467 192 203
Hardy and Littlewood 86 93 131 207 208 246 275 276
Hardy and Wright 139 140
Hasse, H. 35
Hecke 328 338 351
Heilbronn 327 329 350 351
Hilbert, D. 275
Homomorphism 8
Hua 131 242
Identity Theorem 22
Ikehara 94
Ingham, A.E. 130
Jacobi symbol 289 290
Jacobi’s theorem 135 195
Karamata 89
Kronecker, delta 350
Kronecker, symbol 287 289 290 296 299 312 322 338 350
Landau, E. 35 47 56 94 96 130 131
Lattice points 109 278 280 283 284
laurent 73
legendre 39 129 130 355
Legendre symbol 289
Lehmer, D.H. 193 204 205
Lehner 204
Linfoot 350
Linnik, U.V. 242 275
Littlewood 129 130 351
M(a,q) 213
M(n, s, m) 263
m(X) 107
Mellin’s transform 90 345 353
Mertens 320
Minkowski 278 279 281
Modular functions 203
Modular substitution 165 174
Modular transformation 155 159 160 161
Moebius inversion 103 104 133
Mordell 351
Multiplication theorem 23
Multiplicative 4 7 8
Multiplicative function 8
Nagell, T. 35
Natural density 30
p(n) 135
P* 314
Parseval equality 94
Parseval relation 95
Partial integration 14
Partitions, theory of 135—205
Pentagonal number theorem 129
Polya 320
Poussin, de la Vallee see “de la Vallee Poussin”
Prime number theorem 37
Principal character 8
Quadratic law of reciprocity 2 30
r(n) 209
Rademacher 167 169 181 191 193 204 205
Radius of convergence 16 17
Ramanujan 146 181 192 196 203
Region of convergence 14
Riemmann 46 56 57 65 72 130 145 201
Riemmann formula 351 364
Riemmann zeta function 19 37 282 288 294 328
Riemmann — Lebesgue theorem 92 98 123
Riesz 35
Root of unity 9 10 12 145
Rosser, J.B. 130
Roth, K.F. 211
S(a,q) 210
S(h,k) 168
Schnirelman density 275
Schoenfeld, L. 130
Selberg 35 37 128 131
Siegel C.L. 155 167 320 350 351
Siegel theorem 327—342
Sierpinski 129
Skewes 129
Smith, H.J.S. 349
Stieltjes 14
Stirling’s formula 43 358
Sylvester 203
Tatuzawa 131
Tauber 86
Tauberian theorem 47 86 88 93 131
Tchebycheff 45 117 130
Tchudakoff 131
Titchmarsh 35 276
Uniform convergence 17
Uniformly distributed 224
Uspensky and Heaslet 257
Uspensky, J.V. 144 203
van der Corput 215
Van der Monde 349
Vinogradoff 131 206 207 210 211 222 223 241 246 275 276
Waifisz 327
Waring 135
Waring problem 206—276
Watson, G.L. 242 275
Weierstrass 89
Weyl, H. 211 222
Weyl’s method 225—234 243
Whiteman 204
Wiener 60 94
Wilson’s Theorem 37 38
Wright, E.M. 130
Zassenhaus, H. 35
Zeta function 19 20 27 30 56 60 92 131 282 286 328 337 338 342 364
“Circle method” 203
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



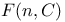


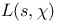


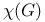

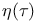

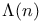
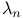
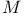

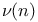
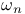


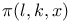
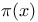
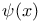



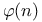


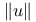
 -function
-function