|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Gromov M. — Metric Structures for Riemannian and Non-Riemannian Spaces |
|
|
 |
| Предметный указатель |
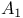 weights B.21.1 weights B.21.1
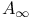 weights, measures B.17 weights, measures B.17
 -flat curves B.14.6 -flat curves B.14.6
 -flat hypersurfaces B.16.1 B.16.2 -flat hypersurfaces B.16.1 B.16.2
Ahlfors ??
Ahlfors regularity B.3.8
Amenable C. C.
Ascoli ?? ??
Avez B. B.
Berger sphere A.
Betti B. A.
Bilipschitz mappings 0
Bishop A. B.2.6
Bounded mean oscillation (BMO) B.11
Calderon — Zygmund approximation B.39
Canonical metric B.
Capacity ( -) C. ?? -) C. ??
Carleson set B.29.4
Carnot — Caratheodory C.
Cocompact C.
Comass C.
Commensurable ??
Compactness B. A. ??
conformal A.
Curvature, growth exponential B.
Curvature, growth polynomial B.
Curvature, pinched ??
Curvature, Ricci A. D.
Curvature, sectional ??
Curvature, short A.
Cusp A.
Degree A.
Diameter A. ??
Dilatation A.
Dimension, Hausdorff ??
Dimension, isoperimetric B.
Distance, Hausdorff A.
Distance, Hausdorff — Lipschitz C.
Distance, Lipschitz A.
Doubling condition, for metric spaces B.2.3
Doubling measures B.3.1
Dyadic cubes B.38
entropy B.
Fibration (Hopf) A.
Flat manifold D.
Flat torus B. ??
Form, differential B.
Form, second fundamental 77
Form, volume A.
g-dimensional, isoperimetric D.
Geodesic B.
Geodesic, minimizing B.
Geodesic, periodic A.
Group, amenable C.
Group, free B.
Group, fundamental C.
Group, Heisenberg B.
Group, Lie 77
Group, nilpotent 77
Group, solvable C.
Hausdorff dimension 77
Hausdorff distance A.
Hausdorff — Lipschitz distance C.
Heisenberg group B. B.2.12
Hoelder continuity B.6.1
Homogeneous space 77 6.8
Hopf fibration A.
Hopf invariant B.
Hurewicz homomorphism C.
Injectivity radius B. ??
| Invariant (Hopf) B.
Isometry (arc-wise) D.
Isoperimetric dimension B.
Isoperimetric inequality B.
Jacobi equation ??
Jacobi field ??
Jacobi variety C.
Jacobian A.
Kaehler manifold D.
Length structure A.
Limit norm ??
Liouville B.
Lipschitz distance A.
Lipschitz function B.2.6
Lipschitzian A.
Loewner A.
Mahler compactness theorem A ??
Margulis lemma D. ??
Mass C.
Maximal functions B.32.1 B.35.1 B.37.3
Metric, canonical B.
Metric, doubling measure B.19.2
Metric, path A.
Metric, quotient ?? ??
Minimal model B.
Minkowski ??
Net C.
Nilpotent group 77
Norm, algebraic C.
Norm, geometric C.
Norm, limit 77
Norm, stable C.
Open at infinity B.
Path metric space B.
Picard B.
Pinched A. ??
Poincare lemma B.
Polyhedron C.
Precompactness A.
Projective space A. D.
Pseudogroup 77
Quasi-isometry (arc-wise) A.
Quasiconvex Appendix A
Quasimetric B.2.1
Quasiminimum D.
Quasiregular A.
Quasisymmetric mappings B.4.1
Quotient, length structure ??
Quotient, metric ??
Rectifiable sets B.24
Regular mappings B.27.1
Ricci curvature A.
Riesz products B.3.10
Sierpinski carpet B.2.11—B.2.12
Sierpinski gasket B.2.11—B.2.12
simplex D. A.
Snowflake functor B.2.8
Spaces of homogeneous type B.8
Stable norm C.
Sullivan B.
Triangulation D. A.
Tube ??
Ultrametric B.2.11
Uniform rectifiability B.25.2 B.25.3
Uniformly perfect sets B.4.3
Vanishing mean oscillation B.10
Variety (Jacobi) C.
Volume A. B. ??
Weak derivatives B.35.2
Weak-type inequality B.32.4
Wirtinger D.
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



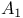 weights
weights 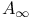 weights, measures
weights, measures  -flat curves
-flat curves