|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Chavel I. — Isoperimetric Inequalities : Differential Geometric and Analytic Perspectives |
|
|
 |
| Предметный указатель |
Measure, inner regular 16
Measure, kinematic, of geodesic flow 127
Measure, locally finite 16
Measure, outer 101
Measure, outer, Borel regular 101
Measure, outer, metric 101
Measure, outer, regular 16 101
Measure, Radon 16
Measure, regular 16
Measure, volume, on graphs 142
Metric, combinatorial 140
Metric, Riemannian 118
Metric, word, on group 141
Milman, V.D. 29
Milnor, J. 143
Model space 124
Model space, isoperimetric inequality in 4
Model space, isoperimetric problem in 4 29
Mollifier 17
Morgan, E. 29 99 116
Moser, J. 183
Mossino, J. 183
Nagy, B.Sz. 221
Narasimhan, R. 29
Nash, J. 183 254
Natural basis of tangent spaces 118
Ndumu, M.N. 224
Nirenberg, L. 183
Noguchi, M. 224
Norm, on group, displacement 141
Norm, on group, word 141
Oprea, J. 51
Orthogonal projection 187
Oshima, Y. 224
Osserman, O. 28 29
Osserman, R. 29
Pang, M. 224
Pansu, P. 248
Payne, L.E. 183
Perimeter 88
Perimeter, geometric 81
Perimeter, set with locally finite 88
Point, critical 18
Principle, Cavalieri 14
Principle, Duhamers 207
Principle, strong maximum, elliptic 19
Principle, strong maximum, parabolic 207
Product Riemannian structure 118
Proner, M.H. 29 224
Qian, Z. 254
Quasi-isometry of metric spaces 140
Quasi-isometry of Riemannian manifolds 128
Rayleigh, Lord 99
Reed, M. 224 254
Reiuey, R.C. 51
Riemann normal coordinates 123
Riemannian distance between points 119
Riemannian manifold 118
Riemannian manifold, discretization of 147
Riemannian manifold, length of path in 119
Riemannian metric 118
Riemannian metric, length of vector in 118
Riesz, E. 221
Rinow, W. 155
Robbins, H. 28
Ros, A. 51
Rough isometry of metric spaces 142
Rudin, W. 29
Saloff-Coste, L. 155 183 184 254
Schmidt, E. 29
Semigroup, one-parameter 190
| Semigroup, one-parameter, contractive 190
Semigroup, one-parameter, generator (infinitesmal) 191
Semigroup, one-parameter, generator (infinitesmal), domain of 191
Sesquilinear form 190
Sesquilinear form, nonnegative 190
Sesquilinear form, semibounded from below 190
Set,  -separated 146 -separated 146
Set, Cacciopoli 88
Set, partition of 15
Simon, B. 224 254
Simon, L. 99 116
Sobolev constant, alternate 180
Sobolev constant, in compact case 162
Sobolev constant, of 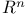 44 45 44 45
Sobolev constant, of graphs 173
Sobolev constant, of Riemannian manifold 131
Sobolev spaces 23
Stein, E.M. 254
Steiner, J. 99
Stroock, D.W. 254
Study, E. 99
Sullivan, D. 224
Surface area 2 3 17 25 31
Symmetric decreasing rearrangement of functions 70
Symmetrization, Schwarz 69
Symmetrization, Steiner 59
Szego, G. 99 183
Takeda, M. 224
Talenti, G. 28 99
Taylor, M. 253
Tensor, curvature 121
Tensor, Ricci 122
Theorem, Alexandrov's 42 51
Theorem, Bishop — Gromov comparison 126
Theorem, Bishop's comparison 126
Theorem, Blaschke selection 55
Theorem, Caratheodory's 101
Theorem, Coulhon extrapolation 241
Theorem, divergence 2-dimensional 9
Theorem, divergence, Riemannian 32 193
Theorem, Federer — Fleming 45 51
Theorem, Federer — Fleming in Riemannian manifolds 131
Theorem, Helly selection 73
Theorem, Lebesgue density 17
Theorem, Liouville's 127
Theorem, maximal 237
Theorem, Mercer's 221
Theorem, Meyers — Serrin 196 224
Theorem, Rademacher 20
Theorem, Radon — Nikodym 16
Theorem, Riesz representation 16
Theorem, Riesz — Thorin interpolation 236
Theorem, Sard 18
Theorem, Spectral 187
Topping, P. 29
Trudinger, N.S. 29 224
Value, critical 18
Value, regular 18
Vanishes at infinity, function that 69
Varopoulos, N.Th, 156 184 224 253 254
Vector field, admissible 82
Vector field, divergence of, on Riemannian manifold 192
Vector field, radial 128
Volume growth 143
Weinberger, H.E. 29 224
Williams, F.L. 224
Wohlrab, O. 28
Yau, S.T. 224
Yau, ST. 131 224 254
Yosida, K. 224
Zalgaller, V.A. 3 28 99
Ziemer, W.P. 29 99
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -separated
-separated