|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Lieberman G.M. Ч Second Order Parabolic Differential Equations |
|
|
 |
| ѕредметный указатель |
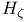 condition 236Ч238 253Ч254 318 condition 236Ч238 253Ч254 318
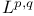 spaces 121 129 130 154 229 spaces 121 129 130 154 229
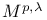 spaces see УMorrey spacesФ spaces see УMorrey spacesФ
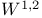 solution 30Ч41 solution 30Ч41
Barrier 38
Barrier, global 38Ч40
Barrier, local 40
Barrier, local, from earlier time 92 231Ч257 397 408 413
Barrier, local, two-sided 40
Bellman equations 363 375 382
Boundary point lemma 12
Brouwer fixed point theorem 204
Calderon Ч Zygmund decomposition 159Ч161 189
Campanato space 49Ч51
Campanato space, equivalent to Holder space 50Ч51 61Ч62
Caristi fixed point theorem 208Ч210
Cauchy Ч Dirichlet problem for fully nonlinear equations 369Ч378 381 385Ч420
Cauchy Ч Dirichlet problem for linear equations 36Ч41 77Ч78 89Ч95
Cauchy Ч Dirichlet problem for quasilinear equations 219Ч320
Comparison principles 13 37 159 188 219Ч222 363Ч364
Conormal problems 137Ч140 179 324Ч341 346Ч347 355Ч356
Contraction mapping principle 29
Convex-increasing domain 238Ч241 317 413Ч414
Cube decomposition see УCalderon Ч Zygmund decompositionФ
Curvature conditions 243Ч247
Cylinder condition 233Ч234
DeGiorgi class 143Ч150
DeGiorgi iteration 144Ч145
Dini continuity 83Ч84
Distance functions, regularized 71Ч72
Distance functions, spatial 241Ч243
Domains with 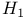 boundary 75 105Ч108 241 boundary 75 105Ч108 241
Domains with 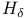 boundary 75Ч79 87Ч89 95 97 243 306Ч307 309 314Ч318 boundary 75Ч79 87Ч89 95 97 243 306Ч307 309 314Ч318
Duality argument 172Ч173
Elliptic part of operator 205
Extension of a function 73Ч74 175 183Ч185 235Ч236 328Ч331 341Ч343
False mean curvature equation 265Ч266 287Ч289 316Ч318
Fully nonlinear equation 361Ч384
Fully nonlinear equation, boundary gradient estimate 389 413Ч414
Fully nonlinear equation, boundary regularity 375Ч378 389
Fully nonlinear equation, Cauchy Ч Dirichlet problem 385Ч420
Fully nonlinear equation, global bound 389 412Ч413
Fully nonlinear equation, global solvability 369Ч371 374Ч375 377 381
Fully nonlinear equation, gradient bound 408
Fully nonlinear equation, gradient estimate 372Ч373 378Ч379 389Ч390 414
Fully nonlinear equation, Holder gradient estimate 373Ч375 379
Fully nonlinear equation, Holder second derivative estimate 365Ч371 377Ч378 400
Fully nonlinear equation, maximum estimate 364 378
Fully nonlinear equation, oblique derivative problem 378Ч381
Fully nonlinear equation, second derivative bounds 391Ч400 409Ч412 414
Fully nonlinear equation, uniformly parabolic 361Ч363 365Ч384
Gateaux variation 211Ч212 370
Global solvability 36Ч41 92Ч93 95Ч97 104Ч108 138 141Ч142 182 185 207Ч208 213Ч215 313Ч318 351 355Ч356 400Ч401 407 412 414
Gradient estimates, boundary 15 62Ч63 170 231Ч257 326Ч346 371
Gradient estimates, global 32Ч33 259Ч266 270Ч271 275Ч276 281 286Ч291
Gradient estimates, Holder 55Ч56 301Ч313 346Ч355
Gradient estimates, local 62Ч63 266Ч269 277Ч289 291Ч294
Harnack inequality for strong solutions 192
Harnack inequality for weak solutions 129
Harnack inequality, weak 186Ч192
Hessian equations 385Ч420
Hessian quotient equations 406Ч407
Holder continuity 129Ч132 134Ч135 140
Holder, continuity 46Ч49
Holder, norm 46Ч47
Holder, norm, weighted 47
Holder, semi-norm 46
Integro-differential equations 19 85 98
Interpolation inequalities 47Ч49 73 174Ч175
Linear parabolic equations (operators), classical solutions, Cauchy Ч Dirichlet problem 77Ч78 87Ч95
Linear parabolic equations (operators), classical solutions, maximum principles 7Ч20
Linear parabolic equations (operators), classical solutions, oblique derivative problem 79 88Ч89 95Ч97
Linear parabolic equations (operators), divergence form see УWeak solutionsФ
Linear parabolic equations (operators), first initial-boundary value problem see УCauchy Ч Dirichlet problemФ
Linear parabolic equations (operators), strong solutions 155Ч201
Linear parabolic equations (operators), strong solutions,  estimates 173Ч185 estimates 173Ч185
Linear parabolic equations (operators), strong solutions, boundary estimates 177Ч185
Linear parabolic equations (operators), strong solutions, boundary regularity 192Ч197
| Linear parabolic equations (operators), strong solutions, Cauchy Ч Dirichlet problem 181Ч183
Linear parabolic equations (operators), strong solutions, global bound 155Ч159
Linear parabolic equations (operators), strong solutions, Holder estimate 192
Linear parabolic equations (operators), strong solutions, Holder estimates 197
Linear parabolic equations (operators), strong solutions, local bound 185Ч186
Linear parabolic equations (operators), strong solutions, maximum principle 155Ч159
Linear parabolic equations (operators), strong solutions, oblique derivative problem 183Ч185
Linear parabolic equations (operators), weak solutions 21Ч43 55Ч56 62Ч67 101Ч154
Linear parabolic equations (operators), weak solutions, boundary regularity 132Ч135
Linear parabolic equations (operators), weak solutions, Cauchy Ч Dirichlet problem 36Ч41 77 104Ч108 141Ч142
Linear parabolic equations (operators), weak solutions, continuous 35Ч43 55Ч56
Linear parabolic equations (operators), weak solutions, global bound 116Ч121 138Ч139
Linear parabolic equations (operators), weak solutions, Holder continuity 129Ч132 134Ч135 140
Linear parabolic equations (operators), weak solutions, local bound 121Ч132
Linear parabolic equations (operators), weak solutions, mixed boundary value problem 65Ч68 140Ч141
Linear parabolic equations (operators), weak solutions, oblique derivative problem 79 142
Local solvability 30Ч36 89Ч92 206Ч207
Maclaurin inequalities 402 406
Marcinkiewicz interpolation theorem 161Ч163
Maximal function 163Ч172
Maximum principles for fully nonlinear equations 364
Maximum principles for linear equations, classical solutions 7Ч20
Maximum principles for linear equations, strong solutions 155Ч159
Maximum principles for linear equations, weak solutions 129 139Ч140
Maximum principles for quasilinear equations 220Ч226 322Ч326
Mean curvature 242Ч244
Mean curvature equation 231 244 265 277 286Ч287 291Ч293 315Ч316 318 339Ч340
Method of continuity 29Ч30 369Ч370
Mixed boundary value problems 140Ч141 179 215Ч216 351
Monge Ч Ampere equation 385 386 407Ч414
Morrey space 130
Morrey space, weighted 56Ч58
Moser iteration 119Ч120 122 143
Newton inequalitites 402Ч403
Newton Ч Maclaurin inequalities 402Ч403 406
Nonlinear boundary condition see УOblique derivative problemФ
Oblique derivative problem for fully nonlinear equations 378Ч381
Oblique derivative problem for linear equations 8 13Ч14
Oblique derivative problem for quasilinear equations 211Ч215 321Ч360
Parabolic frustum 12 13 15 19 41 93 236 239
Paraboloid condition, interior 13 18
Perron process 36Ч41 89Ч93 95Ч96
PoincareТs inequality 28 114Ч116
Pucci operators 362
Quasilinear parabolic equations 203Ч360
Quasilinear parabolic equations, boundary regularity 231Ч257 305Ч309
Quasilinear parabolic equations, Cauchy Ч Dirichlet problem 206Ч208
Quasilinear parabolic equations, conormal problem 324Ч341 346Ч347 355Ч356
Quasilinear parabolic equations, global bounds 220Ч226 322Ч326
Quasilinear parabolic equations, gradient estimate 259Ч299
Quasilinear parabolic equations, gradient estimate, boundary 231Ч257 326Ч346
Quasilinear parabolic equations, Holder gradient estimate 301Ч313 346Ч355
Quasilinear parabolic equations, maximum principle 220Ч226
Quasilinear parabolic equations, oblique derivative problem 211Ч215 321Ч360
Quasilinear parabolic equations, weak solutions 301Ч302 324Ч341 346Ч347 355Ч356
Regular point 38Ч41
Regularized distance see УDistance functions regularizedФ
Schauder estimates, boundary 65Ч67 69Ч71
Schauder estimates, global 75Ч79 141Ч142
Schauder estimates, interior 56Ч60
Schauder estimates, intermediate 74Ч75
Schauder fixed point theorem 205Ч206
Sobolev imbedding theorem 109Ч112
Sobolev inequalities 109Ч114 135Ч137 271Ч275
Sobolev inequalities, weighted 112Ч114 275 327Ч328
Steklov average 102 108 118 126
Strong maximum principle 129
Strong solutions, Cauchy Ч Dirichlet problem 181Ч183
Strong solutions, oblique derivative problem 183Ч185
Subsolution 92 117
Subsolution, strict 387Ч391 393 396Ч397 407 408 412
Supersolution 117
Symmetric function 386 387
Symmetric polynomials 401Ч407
Uniformly parabolic equations, quasilinear 204 253 264 270Ч271 290 292Ч294 313Ч315 318 340Ч346
Vitali Covering Lemma 162Ч163
Weak maximum principle 7Ч9
Weak solutions 101Ч154 221Ч226
Weak solutions,  estimates 165Ч173 177Ч179 estimates 165Ч173 177Ч179
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



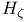 condition
condition 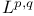 spaces
spaces 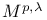 spaces
spaces 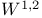 solution
solution 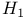 boundary
boundary 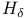 boundary
boundary  estimates
estimates