|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Kolmogorov A.N., Fomin S.V. — Introductory real analysis |
|
|
 |
| Предметный указатель |
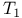 -space 85 -space 85
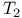 -space 85 -space 85
 -algebra 35 -algebra 35
 -ring 35 -ring 35
 -additivity see “Countable additivity” -additivity see “Countable additivity”
 -algebra 35 -algebra 35
 -finite measure 308 -finite measure 308
 -ring 35 -ring 35
 -neighborhood 46 -neighborhood 46
 -net 98 -net 98
Absolutely continuous charge 347
Absolutely continuous function 336
Absolutely summable sequence 185
Adjoint operator 232
Adjoint operator in Hilbert space 234
Aleph null 16
Alexandroff, P.S. 90 97
Algebra of sets 31
Algebraic dimension 128
Algebraic number 19
Almost everywhere 288
Angle between vectors 143
Arzela’s theorem 102
Arzela’s theorem, generalization of 107
Axiom of Choice 27
Axiom of countability, first 93
Axiom of countability, second 82
Axiom of separation, first 85
Axiom of separation, Hausdorff 85
Axiom of separation, second 85
B-algebra see “Borel algebra”
B-set see “Borel set”
Baire’s theorem 61
Banach space 140
Banach, S. 138 229 238
Base 81
Base, countable 382
Base, neighborhood (local) 83
Basis 121
Basis, dual 185
Basis, Hamel 128
Basis, orthogonal 143
Basis, orthonormal 143
Bessel’s inequality 150 165
Bicompactum 96
Binary relation see “Relation”
Birkhoff, G. 28
Bolzano — Weierstrass theorem 101
Borel algebra 35
Borel algebra, irreducible 36
Borel algebra, minimal 36
Borel closure 36
Borel sets 36
Bounded linear functional 177
Bounded linear functional, norm of 177
Bounded real function 110
Bounded set 65 141 169
Bounded set, locally 169
Bounded set, strongly 197
Bounded set, weakly 197
Cantor function 335
Cantor set 52
Cantor set, points of the first kind of 53
Cantor set, points of the second kind of 53
Cantor — Bernstein theorem 17
Cantor, G. 29
cardinal number 24
Cartesian product see “Direct product”
Cauchy criterion 56
Cauchy sequence 56
Cauchy — Schwarz inequality 38
Chain 28
Chain, maximal 28
Characteristic function 349
Charge 344
Charge, absolutely continuous 347
Charge, concentrated, on a set 346
Charge, continuous 346
Charge, density of 350
Charge, discrete 347
Charge, negative 344
Charge, negative variation of 346
Charge, positive 344
Charge, positive variation of 346
Charge, Radon — Nikodym derivative of 350
Charge, singular 347
Charge, total variation of 346
Chebyshev’s inequality 299
Choice function 27
Classes 6
Classes, equivalence 8
Closed ball see “Closed sphere”
Closed graph theorem 238
Closed set(s) 49
Closed set(s) in a topological space 79
Closed set(s) on the real line 51
Closed set(s), unions and intersections of 49
Closed sphere(s) 46
Closed sphere(s), center of 46
Closed sphere(s), nested (or decreasing) sequence of 59
Closed sphere(s), radius of 46
Closure 46 79
Closure operator 46
Closure operator, properties of 46
Codimension 122
Cohen, P.J. 29
Compact space 92
Compact space, countably 95
Compact space, locally 97
Compactness 92
Compactness, countable 95
Compactness, relative 97
Compactness, relative countable 97
Compactum 92 96
Compactum, metric 96
Complement of a set 3
Complete limit point 97
Complete measure 280
Completely continuous operator(s) 239 ff.
Completely continuous operator(s) in Hilbert space 246—251
Completely continuous operator(s), basic properties of 243—246
Completely regular space 92
Completion (of a metric space) 62
Component (of an open set) 55
Conjugate space 185
Conjugate space of a normed linear space 184
Conjugate space, second 190
Conjugate space, strong topology in 190
Conjugate space, third 190
Conjugate space, weak topology in 200
Conjugate space, weak* topology in 202
Connected set 55
Connected space 84
Contact point 46 79
Continuity 44 87
Continuity from the left 315
Continuity from the right 315
Continuity, uniform 109
Continuous charge 346
Continuous linear functional(s) 175 ff.
Continuous linear functional(s), order of 182
Continuous linear functional(s), sufficiently many 181
Continuum 16
Continuum, power of 16
Contraction mapping(s) 66 ff.
Contraction mapping(s) and differential equations 71—72
Contraction mapping(s) and integral equations 74—76
Contraction mapping(s) and systems of differential equations 72—74
Contraction mapping(s), principle of 66
Convergence almost everywhere 289
| Convergence in measure 292
Convergence in the mean 379
Convergence in the mean square 385
Convergent sequence in a metric space 47
Convergent sequence in a topological space 84
Convex body 129
Convex functional 130 134
Convex hull 130
Convex set 129
Convexity 128
Countability of rational numbers 11
Countable additivity 266 272
Countable base 382
Countable set 10
Countably compact space 95
Countably Hilbert space 173
Countably normed (linear) space 171
Countably normed (linear) space, complete 173
Cover 83
Cover, closed 83
Cover, open 83
Covering see “Cover”
Curve(s) in a metric space 112—113
Curve(s) in a metric space, length of 114 115
Curve(s) in a metric space, sequence of 115
Curve(s), rectifiable 332
Decomposition of a set into classes 6—9
Delta function 124 208
Dense set 48
Dense set, everywhere 48
Dense set, nowhere 48 61
density 350
Derived numbers 318
Derived numbers, left-hand lower 318
Derived numbers, right-hand upper 318
Diameter of a set 65
difference between sets 3
Differentiation of a monotonic function 318—323
Differentiation of an integral with respect to its upper limit 323—326
DIMENSION 121
Dimension, algebraic 128
Dini’s theorem 115
Direct product 238 352
Direct product of measures 354
Directed set 29
Dirichlet function 289 291 301
Discontinuity point of the first kind 315
Discrete charge 347
Discrete space 38
Disjoint sets 2
Disjoint sets, pairwise 2
Distance, between a point and a set 54
Distance, between two sets 55
Distance, properties of 37
Distance, symmetry of 37
Domain (of definition) 4 5 221
Domain (open connected set) 71
Egorov’s theorem 290
Eigenvalue 235
Eigenvector 235
Elementary set 255
Elementary set, measure of 256
Empty set 2
Equicontinuous family of functions 102
Equivalence classes 8
Equivalence relation 7
Equivalent functions 288
Equivalent sets 13
Essential supremum 311
Essentially bounded function 310
Euclidean ?-space 38 144
Euclidean space(s) 138 142
Euclidean space(s), characterization of 160
Euclidean space(s), complete 153
Euclidean space(s), complete, norm of vector in 164
Euclidean space(s), complete, orthogonal elements of 164
Euclidean space(s), components of elements of 149
Euclidean space(s), norm in 142
Euclidean space(s), separable 146
Euler lines 105
Exhaustive sequence of sets 308
Extension of a functional 132
Extension of a measure 271 277 279
Extension of a measure, Jordan 281
Factor space 122
Fatou’s theorem 307
Field 37
Finite expansion 33
Finite function 208
Finite set 10
First axiom of countability 83
First axiom of separation 85
Fixed point 66
Fixed point theorem 66
Fourier coefficients 149 152 165
Fourier series 149 165
Fractional part 8
Fraenkel, A.A. 25 27
Fredholm equation 74
Fredholm equation, homogeneous 74
Fredholm equation, kernel of 74
Fredholm equation, nonhomogeneous 74
Friedman, A. 212
Fubini’s Theorem 359
Function space 39 108
Function(s) 4 ff.
Function(s) of bounded variation 328—332
Function(s), absolutely continuous 336
Function(s), Borel-measurable 284
Function(s), bounded (real) 110 207
Function(s), Cantor 335
Function(s), characteristic 349
Function(s), continuous 44 79
Function(s), continuous, from the left 315
Function(s), continuous, from the right 315
Function(s), continuous, uniformly 109
Function(s), delta 124 208
Function(s), domain (of definition of) 4 5
Function(s), equivalent 288
Function(s), essentially bounded 310
Function(s), finite 207
Function(s), general 5
Function(s), generalized see “Generalized functions”
Function(s), generating 362
Function(s), infinitely differentiable 169
Function(s), integrable 294 296 308
Function(s), integrable, locally 208
Function(s), inverse 5
Function(s), jump 315 341
Function(s), jump of 315
Function(s), left-hand limit of 315
Function(s), lower limit of 111
Function(s), lower semicontinuous 110
Function(s), measurable 284 ff.
Function(s), monotonic 314
Function(s), nondecreasing 314
Function(s), nonincreasing 314
Function(s), one-to-one 5
Function(s), oscillation of 111
Function(s), range of 4 5
Function(s), real 4
Function(s), right-hand limit of 315
Function(s), simple 286
Function(s), singular 341
Function(s), step 316
Function(s), summable 294 296 308
Function(s), test 208
Function(s), uniformly continuous 109
Function(s), upper limit of 111
Function(s), upper semicontinuous 110
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



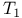 -space
-space 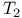 -space
-space  -algebra
-algebra  -additivity
-additivity  -neighborhood
-neighborhood