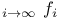|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| J. M. Borwein, Qi.Zhu — Techniques of Variational Analysis (CMS Books in Mathematics) |
|
|
 |
| Предметный указатель |
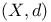 2 2
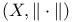 5 5
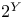 3 3
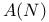 299 299
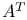 78 78
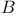 2 2
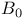 317 317
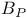 317 317
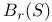 3 3
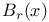 2 2
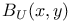 321 321
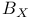 2 2
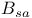 317 317
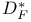 220 220
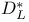 220 220
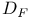 149 149
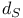 3 3
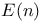 23 23
 166 166
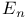 66 66
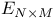 299 299
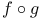 222 222
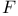 52 52
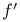 39 39
![$f\ \framebox{\makebox[\totalheight]{\itshape }}\ g$](/math_tex/733d11cdcb1920b7494b0a0e8a1d990882.gif) 3 3
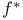 134 134
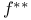 134 134
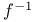 4 4
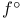 188 188
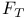 177 177
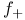 98 98
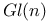 299 299
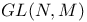 299 299
 243 243
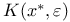 10 10
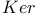 292 292
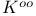 136 136
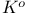 83 83
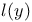 21 21
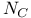 190 190
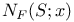 41 41
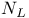 196 196
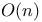 299 299
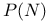 22 302 22 302
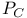 141 141
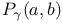 11 11
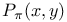 321 321
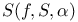 267 267
 299 299
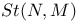 301 301
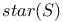 213 213
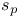 47 47
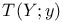 292 292
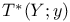 292 292
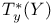 292 292
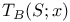 209 209
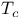 190 190
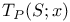 209 209
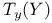 291 291
 318 318
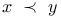 21 21
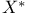 2 2
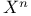 48 48
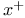 69 69
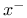 69 69
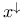 21 21
![$[a, b]$](/math_tex/bd4455e79810acc06e3d31c60fb8bfb282.gif) 299 299
![$[a, C]$](/math_tex/bef8c8a57dd19e6c5b239ae9a09330ee82.gif) 12 12
![$[x, y]$](/math_tex/176b385bbba04cac4d1e9104aa1be4ef82.gif) 15 15
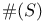 23 23
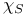 45 45
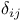 317 317
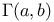 275 275
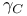 111 111
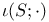 3 3
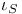 3 3
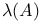 302 302
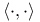 2 2
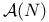 25 25
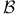 318 318
 223 223
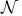 317 317
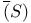 3 3
 3 3
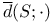 3 3
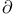 117 117
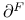 44 44
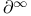 196 196
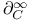 191 191
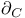 189 189
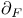 39 39
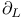 196 196
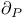 46 46
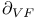 40 40
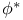 292 292
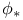 292 292
 292 292
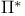 292 292
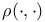 30 30
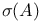 302 302
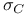 111 111
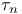 62 62
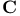 317 317
$](/math_tex/2ddad2a6aa0998ecbed6e5963f7e342e82.gif) 47 47
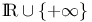 3 3
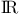 3 3
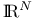 19 19
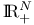 21 21
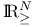 302 302
:doubly stochastic pattern 159
Analytic center 139
approximate chain rule 87 90 93 107
approximate chain rule, strong 87
approximate chain rule, weak 88
approximate critical point 10
approximate extremal principle 104 107 254
approximate Fermat principle 19 20 27
approximate local sum rule 54 71 74 81 87 102 107 197 225 245 253 254
approximate local sum rule, Lipschitz 245
approximate local sum rule, strong 54 57 60 74
approximate local sum rule, strong, failure of 74
approximate local sum rule, weak 57 62
approximate mean value theorem 81 82 83 167 193
approximate multidirectional mean value inequality 95 253 254
approximate multiplier rule 62
approximate multiplier rule, weak 64
approximate nonlocal sum rule 48 51 55 95 105 128 253 254 260
approximate projection 232
Argmin 166
Asplund space 243
Asplund space and Fr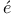 chet smooth space 245 chet smooth space 245
Asplund space, separable 245
Asplund space, subdifferential characterization 254
Asplund space, sum rule characterization 252
asymptotically regular 145
Atlas 291
attainment in Fenchel problems 136
attractive set 89
Baire category theorem 33 203
Banach fixed point theorem 15
bd S 3
Biconjugate 134
Bilinear form 321
Bipolar 136
Birkhoff theorem 25 323
Bishop — Phelps cone 10 59 134
Bishop — Phelps theorem 10
Borwein — Preiss variational principle 30 34
Borwein — Preiss variational principle in finite dimensional spaces 19
Borwein — Preiss variational principle, general form 32
| Borwein — Preiss variational principle, subdifferential form 42
Boundary 3
Bregman distance 149
Bump function 33
bump function, range 36
Canonical projection 292
Caristi — Kirk fixed point theorem 17
Chain rule 87 91 93
chain rule for permutation invariant function 307 310
chain rule for spectral function 307 311
chain rule limiting 198
chain rule on manifolds 296
chain rule smooth 94 297
chain rule, approximate 87 88 90 94 107
chain rule, convex subdifferential 129
Chebyshev set 217
Clarke directional derivative 188
Clarke normal cone 190
Clarke normal cone representation 195
Clarke representation 195
Clarke singular subdifferential 191
Clarke subdifferential 189
Clarke subdifferential maximal 206
Clarke subdifferential of distance function 215
Clarke subdifferential representation 193 195
Clarke tangent cone 190 209
Closed convex hull 3
Closest point 215 239
closest point density 217
Closure 3
Coderivative 220
coderivative chain rule limiting 227
coderivative chain rule strong 226
coderivative sum rule limiting 226
coderivative sum rule strong 224
coderivative sum rule weak 221
coderivative, Fr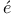 chet 220 chet 220
coderivative, limiting 220
Comparison theorem 50
Concave conjugate 139
Concave function 111
cone bipolar 136
cone monotonicity 83
cone polar 83 136
Conjugation 134
Constrained optimization problem 41 62 65 108 109 190 211 212 298
constrained optimization problem and inequality 69
constrained optimization problem equilibrium constraint 77
constrained optimization problem, multifunction constraint 76
constrained optimization problem, variational inequality constraint 76
Constraint linear 136 139
Constraint qualification 64 66 120 161
constraint qualification calmness 68 72
constraint qualification Mangasarian — Fromovitz 64 67 72
Contingent cone 209
Contraction 15
contraction directional 16
conv S 3
Convex feasibility problem 140
Convex function 111
convex function regularity 192
convex function, difference of 150
convex function, differentiability of 121
convex function, recognizing 124
Convex hull 3
convex multidirectional mean value theorem 130
Convex program 135
convex quasi 83
convex separation 209
convex series(cs) closed 113
convex series(cs) compact 113
Convex set 111
convex subdifferential 117
convex subdifferential calculus 129 135 136
convex subdifferential failure of calculus 134
convex subdifferential sum rule 129
convex subgradient 777 134
convex, normal cone 117
Convexity 80 167
Core 114
core versus interior 116
core(S) 114
Cotangent bundle 292
Cotangent space 292
Cotangent vectors 292
cotangent vectors limit of 293
critical sets 89
cusco 174 190
cusco minimal 174 215
DAD problem 159
DC function 124 214
decoupled infimum 47
decoupling lemma 127 178
decrease principle 97 98
demi-closed 187 184
det(a) 302
Determinant 302
Deville — Godefroy — Zizler variational principle 33
diag 303
diag* 303
diam S 3
Diameter 3 267
Differentiability of convex functions 121
differentiability of distance function 150
differentiability, Fr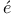 chet 39 243 chet 39 243
differentiability, G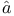 teaux 121 258 330 teaux 121 258 330
Directional contraction 16
Directional derivative 117
directional derivative and subgradients 119
directional derivative of convex function 118
directional derivative sublinear 118
directional derivative, Clarke 188
Distance function 3 38 214 230
dom f 3
Domain 3
domain of subdifferential 117
domain of subdifferential not convex 123
domF 4
Doubly stochastic matrix 23 159
doubly stochastic matrix and majorization 26
Drop 12 95
drop and flower petal 13
drop theorem 13
Dual space 2
duality entropy maximization 157
duality inequalities 150
Duality map 178
Duality pairing 2
Duality weak 135 136
e-lim inf_{i \to \infty}\ f_i$ 170
e-lim sup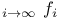 171 171
e-lim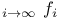 171 171
Eigenvalue function 38 312
eigenvalue largest 77
eigenvalue mapping 302 320
Ekeland variational principle 6 14
Ekeland variational principle alternative forms 8
Ekeland variational principle and Bishop — Phelps theorem 14
Ekeland variational principle and completeness 14
Ekeland variational principle geometric picture 5
Enlargement 3
Entropy maximization 157 159
entropy maximization duality 157 161
entropy maximization in infinite dimensional space 161
Entropy maximum 137 139
entropy, Boltzmann — Shannon 149 158
epi f 3
Epi-convergence 170
epi-limit 171
epi-limit characterization 171
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



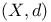
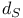
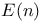

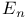
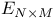
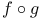
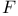
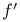
![$f\ \framebox{\makebox[\totalheight]{\itshape }}\ g$](/math_tex/733d11cdcb1920b7494b0a0e8a1d990882.gif)
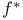
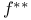
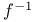
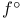
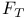

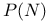
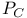
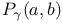
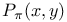

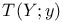
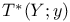
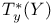
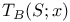

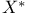
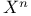
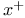
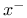
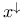
![$[a, b]$](/math_tex/bd4455e79810acc06e3d31c60fb8bfb282.gif)
![$[a, C]$](/math_tex/bef8c8a57dd19e6c5b239ae9a09330ee82.gif)
![$[x, y]$](/math_tex/176b385bbba04cac4d1e9104aa1be4ef82.gif)
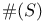
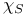
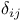
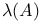
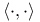
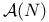
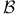


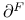
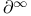
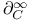
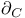
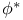
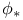

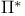
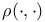
$](/math_tex/2ddad2a6aa0998ecbed6e5963f7e342e82.gif)
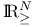
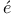 chet smooth space
chet smooth space 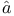 teaux
teaux